2018-02-14
1959
Образованию
Санкт-Петербургский государственный горный институт им Г.В. Плеханова
(технический университет)
Кафедра информатики и компьютерных технологий
Эконометрика
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Часть 1
Методические указания для выполнения лабораторных работ
для студентов специальности 080109
«Бухгалтерский учет, анализ и аудит»
САНКТ-ПЕТЕРБУРГ
2008
Федеральное агентство по образованию
Санкт-Петербургский государственный горный институт им Г.В. Плеханова
(технический университет)
Кафедра информатики и компьютерных технологий
Эконометрика
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Часть 1
Методические указания для выполнения лабораторных работ
для студентов специальности 080109
«Бухгалтерский учет, анализ и аудит»
САНКТ-ПЕТЕРБУРГ
2008
УДК 519.86:622.3.012 (075.83)
ЭКОНОМЕТРИКА. Ч1. Элементы теории вероятностей и математической статистики.
|
|
|
Методические указания для выполнения лабораторных работ для студентов специальности 080109 / СПГГИ(ТУ). Сост.: В.В. Беляев, Т.А. Виноградова, Т.Р. Косовцева,. СПб, 2008., 72 с.
Методические указания содержат необходимые теоретические сведения по выполнению лабораторных работ по эконометрике. Приведены необходимые теоретические сведения и примеры выполнения заданий по некоторым разделам теории вероятностей и математической статистики, которые являются теоретической основой применения эконометрических методов. Все решения выполнены с использованием электронных таблиц MS Excel, в том числе с применением надстройки «Пакет анализа».
Методические указания предназначены для студентов специальности «Бухгалтерский учет, анализ и аудит» дневной формы обучения.
Табл.4. Рис.38. Библиогр.: 3 назв.
Научный редактор - доц. Н.Я. Головенчиц.
© Санкт-Петербургский государственный горный институт им. Г.В.Плеханова, 2008 г.
ВВЕДЕНИЕ
Эконометрика – наука о применении статистических методов в экономическом анализе для проверки правильности экономических теоретических моделей и способов решения экономических проблем.
Основной целью эконометрики является модельное описание конкретных количественных взаимосвязей, обусловленных общими качественными закономерностями, изученными в экономической теории.
Области применения эконометрических моделей напрямую связаны с целями эконометрического моделирования, основными из которых являются:
1) анализ экономических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы;
|
|
|
2) прогноз различных возможных сценариев социально-экономического развития анализируемой системы.
В качестве анализируемой экономической системы могут выступать страна в целом, регионы, отрасли и корпорации, а также предприятия, фирмы и домохозяйства.
Основными типами эконометрических моделей являются
· регрессионные модели с одним уравнением,
· модели временных рядов,
· системы одновременных уравнений.
Термин эконометрика в буквальном переводе означает «измерение в экономике». Этот термин впервые был введен норвежским ученым Рагнаром Фришем в 1926 году. На настоящий момент известно множество других определений термина эконометрика. Широко известно определение эконометрики, предложенное известным российским ученым С.А. Айвазяном.
Эконометрика – это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе
· экономической теории,
· экономической статистики,
· математико-статистического инструментария
придавать конкретное количественное выражение общим качественным экономическим закономерностям, обусловленным экономической теорией.
Для изучения эконометрики необходимы базовые знания по высшей математике, теории вероятностей, математической статистике и экономической теории.
В первой части настоящих методических указаний рассматриваются свойства некоторых видов распределений, в том числе распределений, широко применяемых в эконометрических исследованиях. Также рассматриваются основы выборочного метода в математической статистике. Рассмотрены вопросы применения наиболее известных критериев для проверки статистических гипотез.
Применение эконометрических методов на практике невозможно без использования современного программного обеспечения – пакетов прикладных программ (ППП). К таким пакетам относят как статистические программы общего назначения (Statistica, SPSS, Statgraphics, Instat), так и специализированные эконометрические пакеты (EViews, TSP, STATA, Microfit).
В настоящем лабораторном практикуме в качестве инструментария для расчетов использованы электронные таблицы MS Excel. MS Excel не является специализированным статистическим пакетом, но имеет в своем составе надстройку «Пакет анализа», которая позволяет решать ряд основных статистических (эконометрических) задач. Использование этого средства предполагает проведение значительного объема вычислений «вручную», что позволяет более детально ознакомиться с сутью статистических методов и «начинкой» эконометрических моделей. Существенными доводами за использование MS Excel является его доступность и то, что студенты обычно достаточно хорошо владеют электронными таблицами и широко применяют их для обработки данных. Все это позволяет сосредоточиться на предметной области решаемых задач, а не тратить время на изучение приемов работы с пакетом.
.
Лабораторная работа 1.
Тема. Вычисление числовых характеристик дискретной случайной величины.
Цель: освоить на практике нахождение с помощью MS EXCEL числовых характеристик дискретных случайных величин, а также изучить основные свойства функции распределения.
1.1. Базовые понятия.
Различают дискретные и непрерывные случайные величины (СВ).
Дискретной случайной величиной называют такую СВ, которая принимает отдельные, изолированные значения с определенными вероятностями. Например, число покупателей в магазине в определенный момент времени, количество определенного товара, продаваемого ежедневно в магазине, число автомобилей на проспекте и т. д. являются дискретными СВ. Дискретность распределения не означает его конечность. Существуют дискретные распределения, которые имеют бесконечное количество возможных исходов. Одним из них является распределение Пуассона.
|
|
|
Для описания дискретной СВ необходимо установить соответствие между всевозможными значениями СВ и их вероятностями. Такое соответствие называется законом распределения дискретной СВ. Его можно задать таблично, аналитически (в виде формулы), либо графически.
Например, табличное задание закона распределения дискретной СВ (табл.1.1):
Таблица 1.1
| х | х1 | х2 | … | хn |
| рi | р1 | р2 | … | рn |
где хi – значение случайной величины ;
р1- вероятность, с которой СВ принимает значение хi .
При этом должны выполняться следующие соотношения
и 
(1.1)
Эта таблица показывает что, случайная величина X в результате испытания может принять одно из возможных значений х 1, х 2, ..., хп с соответствующими вероятностями
Р (Х = х 1) = р 1; Р (Х = х 2) = р 2; … Р (Х = хп)= рn. (1.2)
Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной декартовой системе координат строят точки с координатами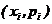 
и соединяют их последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения (полигоном) случайной величины X.
Случайные величины описываются некоторыми числовыми характеристиками. Важнейшими из них являются: математическое ожидание, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Математическое ожидание М(Х) для дискретной СВ определяется по формуле:
, (1.3)
Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений СВ при многократной реализации случайной величины.
Дисперсией D(X) CВ X называется математическое ожидание квадрата отклонения СВ от ее математического ожидания:
(1.4)
При этом для дискретной СВ имеем:
(1.5)
На практике, для вычисления дисперсии используется формула
|
|
|
(1.6)
Следует помнить, что формула (1.4) - это определение дисперсии, а соотношение (1.6) - это свойство, которое доказывается в теории вероятностей.
Из определения дисперсии следует, что это мера рассеяния (разброса) всех возможных значений случайной величины относительно среднего ожидаемого значения. Дисперсия характеризует изменчивость случайной величины: чем она больше, тем дальше от среднего значения находятся возможные значения случайной величины.
Так как дисперсия имеет размерность, равную квадрату размерности СВ, а это неудобно, то вводится другая числовая характеристика - среднее квадратическое отклонение.
Средним квадратическим отклонением или стандартным отклонением - 
СВ Х называют величину:
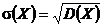(1.7)
Для оценки разброса значений СВ в процентах относительно ее среднего значения, вводится коэффициент вариации V(Х):
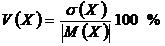(1.8)
Все эти величины (дисперсия, среднее квадратическое отклонение, коэффициент вариации) являются мерой разброса значений СВ относительно среднего значения.
Характеристики рассеяния значений СВ обычно применяются при изучении риска различных действий со случайным исходом: в финансовом анализе при оценивании различных активов и портфеля активов, при анализе риска инвестирования.
Например, если сравнивают две случайные величины, то та СВ, которая имеет большую дисперсию и среднее квадратическое отклонение, более вариабельна (изменчива). Риск, ассоциируемый с инвестициями, часто измеряют стандартным отклонением возврата инвестиций. Если сравниваются два типа инвестиций с одинаковой ожидаемой средней величиной возврата, то инвестиции с более высоким средним квадратическим отклонением считаются более рискованными (хотя более высокое стандартное отклонение предполагает более вариабельный возврат с обеих сторон – как ниже, так и выше средней).
Модой 
дискретной СВ называется её наиболее вероятное значение.
Геометрическая интерпретация моды: мода это абсцисса той точки полигона распределения, у которой ордината максимальна
Определение функции распределения для дискретной СВ:
Функцией распределения СВ Х называется функция F(x), которая определяется следующим образом:
, (1.9)
то есть это вероятность того, что СВ Х принимает значение меньшее, чем фиксированное действительное число x. При изменении значения х изменяются вероятности 
, поэтому функцию F(x) рассматривают как функцию переменной величины.
Согласно определению функции распределения (1.9), имеем следующие соотношения:
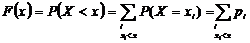, (1.10)
т.е. суммирование распространяется на все значения индекса i, для которых хi < x.
С учетом этого, функцию распределения F(x) для дискретной СВ, принимающей конечное число значений (табл.1.1), можно записать в следующем виде:
(1.11)
График функции F(x) дискретной случайной величины – прерывистая ступенчатая линия.
Отметим некоторые важнейшие свойства F(x):
1. Область значений (изменения) функции 
.
2. F(x) - неубывающая функция, то есть
.
3. 
.
4. F(x) – функция непрерывная слева, т.е. 
5. Если СВ Х принимает значения на отрезке [α,β], то 
6. 
(1.12)
Эти свойства (кроме свойства 4) справедливы и для непрерывной СВ.
Соотношение (1.12) используют для вычисления вероятности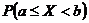 
- вероятности события, при котором случайная величина принимает значения большие или равные а, но меньшие b. Для дискретной СВ эту вероятность можно вычислить, используя непосредственно таблицу распределения, т.е. просто сложить соответствующие вероятности 
.
Пример 1.1.
Каждый урок учитель опрашивает у доски несколько учеников. Число опрошенных учеников зависит от многих факторов: планов на урок, сложности материала, уровня готовности учеников и т. д. Пусть X – число опрошенных учеников в определенный день. X – случайная величина, которая может быть только целым числом. Как показывает практика, число опрошенных учеников не превосходит 5. В нашем примере случайная величина X принимает значения 0; 1; 2; 3; 4; 5, и вероятности этих значений равны 0,1; 0,2; 0,3; 0,2; 0,1; 0,1 соответственно (табл.1.2).
Таблица 1.2
Ряд распределения случайной величины X
| xi | 0 | 1 | 2 | 3 | 4 | 5 |
| P (xi) = pi | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 | 0,1 |
Поскольку появление различных значений случайной величины X – несовместные события, то вероятность того, что число опрошенных на уроке учеников равно 2или 3, равна сумме вероятностей этих значений СВ Х (по теореме сложения вероятностей). Тогда P (Х =2 или Х =3) = P (Х =2) + P (Х =3) = 0,3 + 0,2 = 0,5.
Вероятность того, что число опрошенных на уроке учеников будет находиться в пределах от 1 до 4 (включая 1 и 4), равна 0,8, т.к. P (1≤ X ≤4) = P (Х =1) + P (Х =2)+ P (Х =3) + P (Х =4) = 0,8. Вероятность того ни один ученик не будет опрошен P (X =0)= 0,1.
Задание:
1). Построить многоугольник (или полигон) распределения СВ X – числа опрошенных учеников.
2). Построить функцию распределения СВ X числа опрошенных учеников.
3). Используя функцию распределения, найти вероятность того, что число опрошенных на уроке учеников будет не меньше одного,но меньше трех, т.е. Р(1 ≤ Х < 3).
Решение .
1). Построение многоугольника (полигона) распределения СВ X – число опрошенных на уроке учеников приведено на рис.1.1..
Рис.1.1. Полигон распределения для данных примера 1.1.
2). Построение F (х) -функции распределения СВ X – числа опрошенных на уроке учеников.
По определению . Как следует из табл.1.2. случайная величина Х непринимает значений, меньших 0. Следовательно, если х < 0, то событие X < х невозможно, а вероятность его равна нулю. Для всех значений х, удовлетворяющих двойному неравенству 0 ≤ x < 1, функция F (х)означает вероятность события X < 1. Но случайная величина X принимает значение меньшее 1 лишь в одном случае: значение 0 с вероятностью 0,1.
Если значение х удовлетворяет двойному неравенству, 0 ≤ х < 2, то F (х) = P (Х =0) + P (Х =1) = 0,1 + 0,2 = 0,3.
Пусть, например, х = 2. Тогда F (2)есть вероятность события X < 2. Это событие возможно в двух случаях: случайная величина X принимает значение 0 (с вероятностью 0,1), или 1 (с вероятностью 0,2). Применив теорему сложения вероятностей, получим F (2) = P (Х =0 и Х =1) = 0,1 + 0,2 = 0,3. Аналогичные рассуждения позволяют найти функцию распределения для данных табл. 1.1. Результат приведен в табл. 1.3.
Функция распределения (интегральная функция распределения) для примера 1.1 приведена в таблице 1.3.
Таблица 1.3
| x | 
| 
| 
| 
| 
| 
| 
|
| F (х) | 0 | 0,1 | 0,3 | 0,6 | 0,8 | 0,9 | 1,0 |
На рис.1.2. представлен график функции распределения F (x). Функция распределения F (x)– неубывающая функция, её значение равно единице при х, большем наибольшего возможного значения случайной величины или равном ему (рис.1.2).
Рис.1.2. График функции распределения F (x).
График F (x) имеет ступенчатый вид. Функция распределения каждой дискретной случайной величины постоянна на интервалах и имеет скачки на границах, соответствующих значениям СВ. Величина скачков равна вероятностям конкретныx значений СВ (табл. 1.3).
3). Как следует из таблиц 1.2. и 1.3, вероятность того, что число опрошенных на уроке учеников в определенный день будет меньше трех, можно найти по формуле Р (Х < 3) = F (3) = 0,6. С другой стороны, эту же вероятность можно найти. используя по теорему сложения вероятностей:
Р (Х < 3) = P (Х=0 или Х=1 или Х=2) = 0,1 + 0,2 + 0,3 = 0,6.
Вероятность того, что на уроке будет опрошено не менее одного ученика, когда вероятность события X ≥ 1 вычисляется по формуле
P (X ≥ 1) = 1– P (X < 1) = 1 – 0,1 = 0,9
где P (X < 1) вероятность того, что на уроке будет опрошено менее одного ученика, т.е. не будет опрошен ни один ученик. Вероятность события P (X ≥ 1) также можно найти по формуле
P (X ≥ 1) = 1– P (X < 1) = 1– F (1) = 1 – 0,1 = 0,9
Вероятность того, что число опрошенных учеников в определенный день будет не меньше одного, но меньше трех,можно найти по формуле Р (1 ≤ Х <3) = F (3)– F (1) = 0,6 – 0,1 = 0,5.
Этот же результат может быть получен непосредственно по ряду распределения СВ Х (табл.1.2):
Р (1 ≤ Х <3)= P (X =1)+ P (X =2)=0,2+0,3=0,5
1.2. Биноминальное распределение
Допустим, что выполняется серия из n независимых одинаковых испытаний. Испытания независимы в том смысле, что результаты одних испытаний не влияют на результаты других. Некоторые испытания дают некоторый исход, другие не дают того же результата. Будем называть интересующий нас исход событием U. Если вероятность наступления случайного события в каждом испытании постоянна и равна p, то вероятность того, что при n испытаниях событие U осуществится ровно m раз, определяется формулой Бернулли:
(1.13)
Закон распределения СВ Х, которая может принимать значение 
, вероятности которых определяются формулой Бернулли, называется биноминальным.
Ниже приведены примеры, в которых может использоваться биноминальный закон распределения.
1. Регистрируются n новорожденных, событие U - рождение девочки. Пусть 
- вероятность того, что среди n новорожденных будет m девочек.
2. Проверяется n лотерейных билетов, событие U – выигрыш. Пусть - вероятность того, что среди n билетов будет m выигрышных.
3. На производстве проверяют n изделий, событие U – появление изделия с браком. Пусть - вероятность того, что среди n изделий будет m бракованных.
Математическое ожидание (среднее) биноминального распределения M(X)=np; дисперсия D(X)=npq.
1.3. Распределение Пуассона
Распределение Пуассона является дискретным распределением и описывается формулой
, (1.14)
где λ>0– параметр распределения.
Этот закон используют для описания распределения следующих случайных величин:
1. Пусть на интервале [ 0,N ] оси Ox случайно размещаются n точек, причем события, заключающиеся в попадании одной точки в любой наперед заданный отрезок постоянной (например, единичной) длины, равновероятны.
Если N→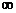 
, n → и 
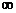, то случайная величина X, равная числу точек, попадающих в заданный отрезок единичной длины (которая может приминать значения 0,1,…k, …), распределяется по закону Пуассона.
2. Если N равно среднему числу вызовов абонентов, поступающих за один час на данную телефонную станцию, то число вызовов поступающих за одну минуту, приближенно распределяется по закону Пуассона с параметром λ= N /60, т.е. вероятность того, что в течении одной минуты будет ровно k вызовов, определяется по формуле (1.14).
Математическое ожидание (среднее) случайной величины Х, распределенной по закону Пуассона равно параметру λ (M(X)=λ), дисперсия также равна λ (D(X)=λ).
Распределение Пуассона является предельным состоянием для биноминального распределения, когда вероятность p события мала (p очень мало). Если число испытаний n велико, то вероятность 
может быть вычислена по формуле
(1.15)
Обозначив через λ = np, заметим, что формулы(1.14) и (1.15) совпадают. Поэтому распределение Пуассона называют законом редких явлений.
Задание
Лабораторная работа №1 содержит три задачи. Все решения провести в MS Excel.
Задача 1
Из n контрольных работ, среди которых k оценены на «отлично», наугад извлекают m работ. Составить закон распределения числа работ, оцененных на «отлично» (случайная величина X) среди отобранных. Построить многоугольник (полигон) распределения. Найти функцию распределения F(x) случайной величины X и построить ее график. Найти среднее значение (математическое ожидание) M(X), дисперсию D(X), среднее квадратическое отклонение 
, коэффициент вариации V(Х) и моду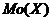 
СВ Х. Найти вероятность 
, где a=x1, b=xn-1. Исходные данные приведены в таблице 1.4.
Таблица 1.4
Варианты заданий
| вариант | n | k | m | вариант | n | k | m |
| 1 | 30 | 5 | 3 | 14 | 30 | 5 | 5 |
| 2 | 30 | 5 | 4 | 15 | 28 | 5 | 4 |
| 3 | 25 | 5 | 3 | 16 | 25 | 5 | 3 |
| 4 | 30 | 6 | 3 | 17 | 26 | 6 | 3 |
| 5 | 30 | 6 | 4 | 18 | 25 | 6 | 4 |
| 6 | 25 | 6 | 3 | 19 | 28 | 6 | 3 |
| 7 | 30 | 7 | 3 | 20 | 29 | 7 | 3 |
| 8 | 30 | 7 | 4 | 21 | 31 | 7 | 4 |
| 9 | 30 | 7 | 5 | 22 | 28 | 7 | 5 |
| 10 | 30 | 7 | 6 | 23 | 27 | 7 | 6 |
| 11 | 25 | 7 | 3 | 24 | 30 | 7 | 3 |
| 12 | 25 | 7 | 4 | 25 | 30 | 7 | 4 |
| 13 | 25 | 5 | 4 | 26 | 27 | 5 | 4 |
Задача 2
Стрелок производит n -выстрелов в цель. Вероятность попадания в цель при каждом выстреле равна р. Составить закон распределения числа попаданий в цель (случайная величина X). Построить многоугольник (полигон) распределения СВ Х. Найти функцию распределения F(x) СВ Х и построить ее график. Найти среднее значение (математическое ожидание) M(X), дисперсию D(X), среднее квадратическое отклонение , коэффициент вариации V(x) и моду 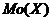СВ Х. Найти вероятность , где a=x1, b=xn-1. Исходные данные приведены в таблице 1.5.
Таблица 1.5
Варианты заданий
| вариант | n | p | вариант | n | p |
| 1 | 3 | 0,25 | 14 | 4 | 0,25 |
| 2 | 4 | 0,3 | 15 | 5 | 0,3 |
| 3 | 5 | 0,4 | 16 | 4 | 0,4 |
| 4 | 5 | 0,25 | 17 | 5 | 0,25 |
| 5 | 3 | 0,35 | 18 | 4 | 0,35 |
| 6 | 4 | 0,4 | 19 | 5 | 0,4 |
| 7 | 5 | 0,25 | 20 | 4 | 0,25 |
| 8 | 5 | 0,3 | 21 | 5 | 0,3 |
| 9 | 4 | 0,4 | 22 | 4 | 0,4 |
| 10 | 5 | 0,25 | 23 | 5 | 0,25 |
| 11 | 3 | 0,5 | 24 | 4 | 0,5 |
| 12 | 4 | 0,4 | 25 | 5 | 0,4 |
| 13 | 5 | 0,6 | 26 | 5 | 0,6 |
Задача 3
Телефонная станция получает в час в среднем n вызовов.
Составить закон распределения количества вызовов, полученных станцией за одну минуту (случайная величина X). Построить многоугольник (полигон) распределения для иллюстрации распределения. Найти функцию распределения F (x) случайной величины X и построить ее график. Найти среднее значение (математическое ожидание) M (X), дисперсию D (X), среднее квадратическое отклонение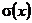 
и моду 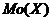СВ Х. Вычисление математического ожидания M (X), дисперсии D (X), среднего квадратического отклонения 
провести двумя способами: приближенно, используя таблицу распределения, взяв первые 20 значений СВ, и аналитически, используя тот факт, что заданное распределение пуассоновское.
Какова вероятность того, что за одну минуту станция получит
а) не менее k и не более m вызовов?
б) менее k вызовов?
в) более m вызовов?
г) менее k вызовов или более m вызовов?
Исходные данные приведены в таблице 1.6.
Таблица 1.6
Варианты заданий
| Вариант | n | k | m | Вариант | n | k | m |
| 1 | 360 | 3 | 7 | 16 | 270 | 2 | 7 |
| 2 | 240 | 3 | 8 | 17 | 360 | 3 | 8 |
| 3 | 270 | 5 | 8 | 18 | 240 | 2 | 7 |
| 4 | 330 | 3 | 7 | 19 | 330 | 2 | 7 |
| 5 | 360 | 4 | 9 | 20 | 420 | 2 | 7 |
| 6 | 240 | 4 | 9 | 21 | 360 | 5 | 7 |
| 7 | 270 | 3 | 7 | 22 | 240 | 3 | 9 |
| 8 | 330 | 3 | 8 | 23 | 270 | 3 | 8 |
| 9 | 420 | 4 | 9 | 24 | 330 | 3 | 9 |
| 10 | 360 | 2 | 7 | 25 | 420 | 3 | 8 |
| 11 | 240 | 3 | 7 | 26 | 360 | 5 | 8 |
| 12 | 270 | 4 | 9 | 27 | 240 | 4 | 9 |
| 13 | 330 | 5 | 8 | 28 | 270 | 3 | 9 |
| 14 | 240 | 5 | 8 | 29 | 330 | 4 | 9 |
| 15 | 360 | 3 | 9 | 30 | 420 | 3 | 7 |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА 1.
Из 25 контрольных работ, среди которых 5 оценены на «отлично», наугад извлекают 3 работы. Составить закон распределения случайной величины Х - числа работ, оцененных на «отлично», среди отобранных работ. Найти функцию распределения F (x) случайной величины X и построить ее график. Найти для X ее среднее значение (математическое ожидание M (X)), дисперсию D(X), среднее квадратическое отклонение 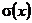и моду . Найти вероятность 
, где a=x2, b=xn-1 двумя способами: используя функцию распределения и непосредственно по таблице распределения.
Решение: Пусть случайная величина X – число работ, оцененных на «отлично» среди трех отобранных. Так как из 25 контрольных работ 5 оценены на «отлично» и выбирается из них 3 работы, то случайная величина X может принимать следующие значения:
Найдем вероятности того, что случайная величина Х примет соответствующие значения. Заметим, что решение задачи о нахождении вероятности события (Х=0), то есть Р(Х=0), как впрочем и решение задач о нахождении следующих вероятностей Р(Х=1), Р(Х=2), Р(Х=3), может быть найдено с помощью известной формулы
где N - общее количество исходов, M – количество исходов, благоприятствующих появлению события А.
В этой задачесобытие А состоит в том, что среди отобранных работ, число работ, оцененных на «отлично», равно k; k последовательно принимает значения 0, 1, 2 и 3; N – количество способов выбора трех работ из 25 - общего количества работ; M – количество способов выбора k работ, оцененных на «отлично», из общего количества работ.
Предварительно найдем число сочетаний из 25 по 3 (число способов, которыми можно из 25 контрольных работ извлечь 3):
Для (X=0) число исходов, благоприятствующих появлению события А, может быть вычислено по формуле
Тогда 
.
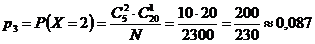
Тогда искомый закон распределения примет вид
| X | 0 | 1 | 2 | 3 |
| pi | 0,496 | 0,413 | 0,087 | 0,004 |
Убедимся, что сумма вероятностей равна единице:
Проведем все эти расчеты в MS Excel.
Математическое ожидание (среднее значение) дискретной случайной величины X найдем по формуле (1.3). Пример реализации в MS Excel дан на рис.1.3, интервал D20:D25.
В результате получаем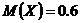 
Дисперсию дискретной случайной величины X найдем двумя способами.
Первый способ - по формуле (1.5), по определению дисперсии. Эти вычисления реализованы в MS Excel (рис.1.3), интервал ячеек F20:F25.
В результате получаем 
Второй способ - по формуле (1.6) по свойству дисперсии. Предварительно необходимо вычислить математическое ожидание квадрата дискретной случайной величины X - 
. Пример реализации в MS Excel дан на рис.1.3, интервал ячеек E20:E25. В результате получаем 
Тогда дисперсия равна
Оба значения, полученные разными способами, совпали.
Среднее квадратическое отклонение:
.
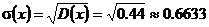Вычислим моду 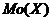. Для этого можно по таблице распределения (интервал B20:C25) найти xi, которому соответствует наибольшее значение вероятности pi.
Другой способ - анализируя полигон распределения, найдем xi, которому соответствует самое большое значение pi. Очевидно, что =0.
Рис.1.3. Решение задачи 1 в MS Excel (начало).
Вычислим коэффициент вариации V(Х) по формуле (1.8):
Построим многоугольник распределения по заданному распределению, используя графические средства MS Excel.
Для нахождения функции распределения воспользуемся формулой (1.11).
В нашем примере имеем:
Таким образом, функция распределения примет вид
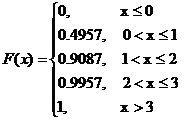
В MS Excel эти расчеты реализованы в интервале ячеек D55:D59 (рис.1.4), на том же листе построена «заготовка» для графика функции распределения. Далее эту «заготовку» следует достроить вручную до корректного графика (нанести стрелки и подписи по оси ординат), как на рис.1.2. Эту операцию по превращению полученной диаграммы EXCEL в корректную функцию распределения необходимо производить для всех распределений в данной работе (рис.1.6 и рис.1.8).
 |
Рис.1.4 Решение задачи 1 в MS Excel (окончание).
Найдем вероятность , где a=x2, b=xn.
В данном случае x2=1, xn=3, т.е. требуется найти 
.
Первый способ - используем функцию распределения:
Второй способ - по таблице распределения.
Событие, состоящее в том, что СВ Х примет значения в промежутке 
может реализоваться только в том случае, когда СВ принимает значения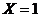 
или 
. Таким образом,
ЗАДАЧА 2.
Стрелок производит три выстрела в цель. Вероятность попадания в цель при каждом выстреле равна 0,2. Составить закон распределения числа попаданий в цель (случайная величина X). Найти функцию распределения случайной величины X F (x) и построить ее график. Найти среднее значение (математическое ожидание) M (X), дисперсию D (X) и моду СВ Х. Найти вероятность 
, где a=x2, b=xn-1 двумя способами: с помощью функции распределения и непосредственно по таблице распределения СВ Х.
Решение:
Пусть случайная величина X – число попаданий в цель при трех выстрелах.
Обозначим n – число выстрелов, р - вероятность попадания при каждом выстреле, q - вероятность промаха при каждом выстреле q =1- р. По условию имеем р=0,2; q=0,8; n=3.
Заметим, что при n=3 случайная величина X может принимать следующие значения: х1=0, х2=1, х3=2, х4=3. Отметим, что испытания проводятся по схеме Бернулли. Действительно, число испытаний конечно и каждое испытание является независимым. В каждом испытании наблюдается либо «успех» (попал в цель), либо «неуспех» (не попал в цель или промахнулся). Вероятность удачи в каждом испытании постоянна. Так как испытания проводятся по схеме Бернулли, то можно утверждать, что случайная величина X имеет биномиальное распределение и соответствующие вероятности вычисляются по формуле Бернулли:
Найдем соответствующие вероятности для данного примера:
Тогда искомый закон распределения примет вид
| X | 0 | 1 | 2 | 3 |
| p | 0,512 | 0,384 | 0,096 | 0,008 |
Убедимся, что сумма вероятностей равна единице:
Заметим, что для биномиального распределения математическое ожидание и дисперсию легко вычислить по формулам:
математическое ожидание M(X)= n p =3· 0,2 =0,6;
дисперсия D(X) = n p q =3· 0,2 ·0,8 = 0,48.
Найдем вероятность , где a=x2, b=xn. В данном случае x2 =1, xn =3, т.е. требуется найти
Первый способ - используя функцию распределения
Второй способ - по таблице распределения.
Событие, состоящее в том, что СВ примет значения в промежутке 
может реализоваться только в том случае, когда СВ равна 1 или 2. Таким образом,
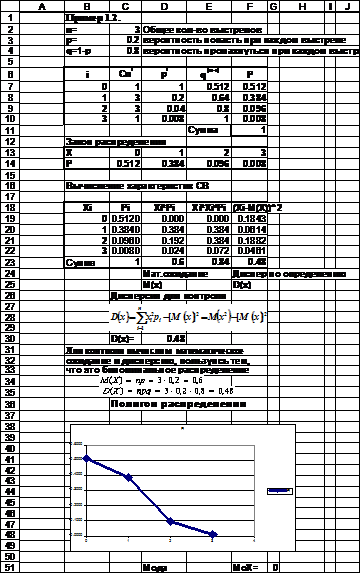
Рис.1.5. Решение задачи 2 в MS Excel
 |
Рис.1.6. Решение задачи 2 в MS Excel (продолжение)
ЗАДАЧА 3.
Телефонная станция получает в час в среднем 300 вызовов.
Составить закон распределения количества вызовов, полученных станцией за одну минуту (случайная величина X). Построить многоугольник (полигон) распределения для иллюстрации распределения СВ X. Найти среднее значение (математическое ожидание M (X)), дисперсию D (X), среднее квадратическое отклонение 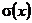и моду СВ X. Вычисление математического ожидания M (X)), дисперсии D (X), среднее квадратического отклонения 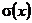провести двумя способами: приближенно, используя таблицу распределения, взяв первые 20 значений СВ, и аналитически, используя тот факт, что рассматривается распределение Пуассона.
Найти функцию распределения F (x) случайной величины X и построить ее график. Какова вероятность того, что за одну минуту станция получит не менее 4 вызовов и не более 8?
Решение.
Проведем все вычисления в MS Excel, рис.1.7-1.8.
Очевидно, что СВ X - количество вызовов, полученных станцией за одну минуту, распределено по закону Пуассона. Определим параметр λ. В данном случае λ= n /60 =300/60=5.
Распределение Пуассона определяется соотношением (1.14), для данной задачи
На рис.1.7 в интервале ячеек A5:B26 представлены первые 20 значений искомого распределения. Ячейка B6 содержит формулу =$C$4^A6/ФАКТР(A6)*EXP(-$C$4), остальные значения этого столбца заполняются копированием.
Вычисление математического ожидания M (X)), дисперсии D (X), среднего квадратического отклонения 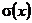выполнено по формулам (1.3)-(1.6). Порядок вычисления такой же, как в задачах 1 и 2. Заметим, что эти формулы в данном случае не являются точными, поскольку случайная величина принимает бесконечное множество значений, а в вычислениях удержаны только 20 первых слагаемых(погрешность можно вычислить самостоятельно).Тогда, M(X)=λ=4,999998; D(X)=λ=4,999978;
.
Аналитически вычислениематематического ожидания M(X), дисперсии D(X), среднего квадратического отклонения 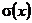исключительно просто.
M(X)=λ=5, D(X)=λ=5, 
.
Сравнивая вычисленные характеристики, приходим к выводу, что результаты совпадают с точностью до 10-5.
Коэффициент вариации V(x):
Данное распределение двумодальное (имеет два одинаковых наибольших значения). Очевидно, что равна 4 и 5.
Многоугольник (или полигон) распределения построен на рабочем листе в строках 35:50.
Найдем приближенно функцию распределения F (x) случайной величины X и построим ее график. Таблица значений функции распределения для первых 12 интервалов приведена в строках 52:67, график функции распределения для первых 12 интервалов приведен в строках 67:89.
Найдем вероятность того, что за одну минуту станция получит не менее 4 и не более 8 вызовов, т.е. найдем 
Первый способ использует функцию распределения:
, тогда
Рис.1.7. Решение задачи 3 в MS Excel (начало).
 |
Рис.1.8. Решение задачи 3 в MS Excel (окончание).
Второй способ использует непосредственно таблицу распределения.
Очевидна следующая формула:
Для вычисления по этой формуле в ячейку H96 введем формулу =СУММ(B10:B14), в результате получим то же значение, равное 0,6669 (рис.1.9).
Рис.1.9. Решение задачи 3 в MS Excel
.
Лабораторная работа 2
Тема. Вычисление числовых характеристик непрерывной случайной величины.
Цель: Освоить на практике вычисление с помощью MS EXCEL числовых характеристик случайной непрерывной величины, изучить основные свойства функции распределения, плотности распределения и применять эти функции для вычисления вероятностей.
2.1. Определение непрерывной случайной величины. Функция распределения непрерывной случайной величины
Непрерывной случайной величиной называют случайную величину, которая может принимать любые значения на числовом интервале.
Примеры непрерывных случайных величин: возраст студентов, длина ступни ноги человека, масса детали и т. д. Это положение относится ко всем случайным величинам, измеряемым на непрерывной шкале, таким как меры веса, длины, времени, температуры, расстояния. Измерение может быть проведено с точностью до какого-нибудь десятичного знака, но такая случайная величина – теоретически непрерывная величина. В экономическом анализе находят широкое применение относительные величины, различные индексы экономического состояния, которые также вычисляются с определенной точностью, скажем, до двух знаков после запятой, хотя теоретически такие величины – непрерывные случайные величины.
У непрерывной случайной величины возможные значения заполняют некоторый интервал (или сегмент) с конечными или бесконечными границами.
Закон распределения непрерывной случайной величины можно задать в виде интегральной функции распределения,являющейся наиболее общей формой задания закона распределения случайной величины, а также в виде дифференциальной функции (плотностираспределения вероятностей),которая используется для описания распределения вероятностей только непрерывной случайной величины.
Функция распределения (или интегральная функция) F (x) – универсальная форма задания закона распределения случайной величины. Для непрерывной случайной величины, как и для дискретной СВ функция распределения определяется соотношением (1.9), т.е. - это вероятность того, что случайная величина X примет значение, меньшее фиксированного действительного числа х.
Принято считать, что случайная величина X известна, если известна ее функция распределения F (x).
Теперь можно дать другое определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция.
2.2. Свойства функции распределения непрерывной случайной величины и её график
Для функций распределения дискретных и непрерывных случайных величин справедливы свойства, приведенные в л.р. 1. Свойство 4 может быть заменено на следующее
F(x) – функция непрерывная, т.е. 
На рис. 2.1 представлен схематический график функции распределения F (х), учитывающий ее свойства.
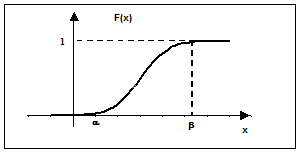
Рис. 2.1. Типичный график функции распределения непрерывной случайной величины
2.3. Плотность распределения вероятности непрерывной случайной величины (дифференциальная функцияраспределения)
Дифференциальной функцией распределения (плотностью распределения вероятности) непрерывной случайной величины X называют f (x) первую производную от функции распределения F (x):
f (x) = F ′ (x) (2.1)
Дифференциальная функция применяется только для описания распределения вероятностей непрерывных случайных величин.
2.4. Вероятность попадания непрерывной случайной величины в заданный интервал
Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу [ a,b ], равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b:
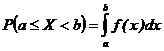. (2.2)
Геометрическая интерпретация этого результата: искомая вероятность равна площади криволинейной трапеции, ограниченной осью ОХ, функцией распределения f (x)и прямыми х = a, х = b.
2.5. Нахождение функции распределения по известной плотности распределения
Зная плотность распределения f (x),можно найти функцию распределения F (x)по формуле
. (2.3)
Согласно равенствам (2.2), (2.3) и свойству 6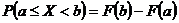 
(л.р. №1) функция распределения F(x) и плотность распределения f (x) связаны так, как показано на рис. 2.2.
..
Рис.2.2. Связь функции распределения с плотностью распределения вероятностей
Используя геометрическую интерпретацию, легко проиллюстрировать следующий факт: вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.
Р (Х = х 1) = 0 (2.4)
Согласно сказанному, равенство нулю вероятности Р (Х = х 1)не всегда означает, что событие Х = х 1невозможно. Говоря о вероятности события Х = х 1, априорно пытаются угадать, какое значение примет случайная величина в опыте.
Если х 1лежит в области возможных значений непрерывной случайной величины X, то с некоторой уверенностью можно предсказать область, в которую случайная величина может попасть. В то же время невозможно хотя бы с малейшей степенью уверенности угадать, какое конкретное значение из бесконечного числа возможных значений примет непрерывная случайная величина.
Например, если метеослужба объявляет, что температура воздуха в полдень составила 5°С, то это не означает, что истинное значение температуры было точно равно этому значению, а температура была приблизительно таковой. Вероятность события, состоящего в том, что температура воздуха в полдень в точности составляет 5°С, равна нулю.
Таким образом, для полной характеристики непрерывной случайной величины достаточно задать функцию распределения или плотность ее вероятности.
2.6. Свойства плотности распределения (дифференциальной распределения)
1. Дифференциальная функция – неотрицательная функция:
f (x)≥ 0,
