Экспоненциальное распределение

Случайная величина распределена экспоненциально с параметром l.

1. Построить графики плотности распределения и функции распределения, построив таблицу значений функции при изменении x от 0 до b c шагом h=b/N, при N =40. Таким образом, таблица будет содержать 41 значение. Значение b подобрать самостоятельно, так, чтобы таблица была содержательной, т.е. F(b) было достаточно близко к 1, a f(b) достаточно близко к 0, ишаг h был достаточно мал. Если это не удается сделать при N =40, увеличьте N.

Таблицу построить двумя способами:

a) пользуясь непосредственным определением функции плотности и функции распределения СВ;

b) пользуясь встроенной функцией ЭКСПРАСП().

2. Используя приемы приближенного интегрирования, проверить соотношения (2.6), (2.19) для заданного распределения. Вычислить погрешности.

Вычислить вероятности следующих событий:

1). Случайная величина принимает значение меньше 1/l.

2). Случайная величина принимает значение больше 1/l.

3). Случайная величина принимает значение больше 1/l и меньше 2/l

4). Случайная величина принимает значение меньше 1/l или больше 2/l.

Используя графики функций плотности распределения f(x) и распределения F(x), построенные в п.1, проиллюстрируйте полученный результат.

Исходные данные для различных вариантов составляются по следующему правилу:

l =k+(n/ 10 );

где k – номер подгруппы в потоке; n - номер студента в списке.

Задача 3

Построить графики плотности вероятности для следующих распределений:

1) распределение χ² (хи – квадрат);

2) распределение Стьюдента (t- распределение);

3) распределение Фишера (F -распределение) для нескольких степеней свободы.

Сделать выводы о симметричности распределений в зависимости от числа степеней свободы.

При фиксированном числе степеней свободы найти односторонние критические значения для следующих значений p: 0,05; 0,025 и 0,01.

Сделать выводы об изменении критических значений в зависимости от величины p -значений.

Для распределения Стьюдента вычислить двусторонние критические значения для тех же p -значений. Сделать соответствующие иллюстрации.

Данные для построения распределений (число степеней свободы) подобрать самостоятельно.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ЗАДАЧА 1

1. Пусть случайная величина Х распределена нормально с параметрами m =0 и σ=1. Все вычисления приведены на рис.2.4 и рис.2.5.

а) Столбец С содержит значения функции плотности распределения, найденные по определению этой функции по формуле (2.13).

b) Столбец D содержит значения функции плотности распределения, найденные с помощью встроенной функцией НОРМРАСП().

Эта встроенная функция возвращает значения, связанные с нормальным распределением для указанного среднего и стандартного отклонения.

Синтаксис: НОРМРАСП(x; m; sigma; logical),

где x — значение, для которого вычисляется значения функций F (x) и f (x);

m и sigma — параметры распределения;

logical — логическое значение, определяющее форму функции. Если logical имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

2. Столбец E содержит значения функции распределения F (x), найденные с помощью встроенной функцией НОРМРАСП(). На рис.2.6. показаны графики построенных функции распределения и функции плотности.

3. Результаты вычислений для пункта 3 представлены в строках 51:57. На рис.2.7. приведены соответствующие иллюстрации, площади заштрихованных криволинейных трапеций равны искомым вероятностям.

4. Для проверки соотношения (2.6), необходимо вычислить, интеграл ,

а в случае m =0 и σ =1, интеграл

Поскольку аналитическое вычисление интеграла путем нахождения первообразной невозможно, вычислим интеграл, используя приемы приближенного интегрирования. Принимая во внимание, что большая часть распределения сосредоточена в интервале от -3 σ до 3 σ, справедливо следующее соотношение .

Чтобы найти численно последний интеграл, воспользуемся формулой трапеций

, (2.28)

где

Вычисление этого интеграла приведено на рис.2.4 и 2.5. Подынтегральной функцией является функция f(x). В интервале F8:F48 содержатся слагаемые для вычисления выражения в квадратных скобках формулы 2.28. В ячейке F49 содержится сумма всех слагаемых, в ячейке G60 содержится приближенное значение интеграла, вычисленного по формуле (2.28), оно равно 0,999933. Теоретическое значение этого интеграла равно 1, таким образом, абсолютная погрешность вычисления равна 10^-4.

Для приближенного вычисления математического ожидания, определяемого формулой (2.7), необходимо воспользоваться формулой (2.28), взяв в качестве подынтегральной функции функцию х f(x ). Все промежуточные вычисления содержатся в интервале G8:G49. В ячейке G62 содержится приближенное значение этого интеграла, вычисленного по формуле (2.28), равное 0,000000. Теоретическое значение математического ожидания равно нулю (a = 0), таким образом, абсолютная погрешность равна 10^-6.

Для приближенного вычисления дисперсии, определяемой формулой (2.8), необходимо воспользоваться формулой (2.28), взяв в качестве подынтегральной функции .

Все промежуточные вычисления содержатся в интервале H8:H49. В ячейке G64 содержится приближенное значение интеграла, вычисленного по формуле (2.28), равное 0,998816. Теоретическое значение дисперсии равно σ²=1, таким образом абсолютная погрешность равна 10^-3.

Рис.2.4. Рабочий лист в режиме отображения данных

Рис.2.5. Рабочий лист в режиме отображений формул

Рис.2.6 Графики плотности и функции распределения для нормального распределения.

Рис.2.7 Геометрический смысл вычисления вероятности попадания СВ в интервал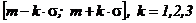

Задача 2.

В отделение банка приходит n клиентов в час. Известно, что промежуток времени между приходами двух клиентов распределен по экспоненциальному закону распределения. Исследовать этот закон распределения при заданной интенсивности, выполнив следующие действия:

1. Составить таблицу значений функции плотности распределения и функции распределения при изменении значений x от 0 до b c шагом h=b/N, при N =40. Построить графики этих функций. Значение b подобрать самостоятельно таким образом, чтобы таблица была содержательной, т.е. F(b) было достаточно близко к 1, a f(b ) достаточно близко к 0, ашаг h был достаточно мал.

Таблицу построить двумя способами:

a) пользуясь непосредственным определением функции плотности и функции распределения;

b) пользуясь встроенной функцией ЭКСПРАСП().

3. Предположим, что в банк уже пришел один клиент.

a) какова вероятность того, что следующий клиент придет не ранее, чем через 12 мин и не позже, чем через 24 мин?

b) какова вероятность того, что следующий клиент придет в течение 12 мин?

c) какова вероятность того, что следующий клиент придет позже, чем через 24 мин?

Используя графики функции плотности распределения f(x) и функции распределения F(x), проиллюстрируйте полученный результат. Приведем решение при n =5.

Решение задачи при n =5.

По определению интенсивности, в данном случае λ = 5.

Построим таблицу значений функции при изменении x от 0 до 2 σ c шагом h =0,05. Т.е. таблица будет содержать 41 значение.

Все построения приведены на рис.2.8 - 2.10.

а) Столбцы В и С содержат значения функции плотности распределения и функции распределения, вычисленных по определению (2.18), (2.17).

b) Столбцы D и Е содержат значения тех же функций, вычисленных с помощью встроенной функцией ЭКСПРАСП().

Эта встроенная функция возвращает значения, связанные с экспоненциальным распределением для значения параметра λ.

Синтаксис: ЭКСПРАСП(x; lyambda; logical)

где

x — значение, для которого строится распределение;

lyambda — это значение параметра распределения;

logical — логическое значение, определяющее форму функции. Если logical имеет значение ИСТИНА, то функция ЭКСПРАСП возвращает интегральную функцию распределения, если аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

Искомые графики приведены на рис.2.10.

2. Для того чтобы проверить соотношение (2.6), необходимо вычислить интеграл

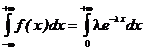
т.к. λ =5, вычисляем интеграл

Принимая во внимание, что большая часть распределения сосредоточена в интервале от 0 до 2 (для данного λ), справедливо следующее соотношение

Чтобы найти последний интеграл, воспользуемся приближенной формулой трапеций. (2.28).

Вычисление этого интеграла приведено на рис.2.8 и 2.9. Подынтегральной функцией является функция f(x). В интервале F7:F47 содержатся слагаемые для вычисления выражения в квадратных скобках из формулы (2.28). В ячейке F48 содержится сумма всех слагаемых, в ячейке F58 содержится приближенное значение интеграла, вычисленного по формуле (2.28), т.е. 1,005157.

Теоретическое значение этого интеграла равно 1, таким образом, абсолютная погрешность вычислений равна 0.005.

Для приближенного вычисления математического ожидания (2.7) используем (2.28), взяв в качестве подынтегральной функции функцию х f(x). Все промежуточные вычисления содержатся в интервале G7:G47. В ячейке F60 содержится приближенное значение интеграла, вычисленного по формуле (2.28), т.е. 0,198861.

Теоретическое значение математического ожидания равно 1/ λ =0.2, таким образом, абсолютная погрешность вычислений равна 0,001.

Для приближенного вычисления дисперсии (2.8) необходимо воспользоваться формулой (2.28), взяв в качестве подынтегральной функции функцию . Все промежуточные вычисления содержатся в интервале H7:H48. В ячейке F62 содержится приближенное значение интеграла, вычисленного по формуле (2.28), т.е. 0.040453.

Теоретическое значение дисперсии распределения равно (1/ λ)²=(0.2)²=0.04, таким образом, абсолютная погрешность вычислений равна 0,004.

Рис.2.8 Рабочий лист в режиме отображения данных

Рис.2.9. Рабочий лист в режиме отображения формул

Рис.2.10. Графики плотности и функции распределения для экспоненциального распределения

3. Чтобы вычислить вероятность того, что следующий клиент придет не ранее, чем через 12 мин и не позже, чем через 24 мин, необходимо сначала перевести минуты в часы, поскольку в качестве интенсивности используется количество посещений в час. При этом 12 мин - это 0,2 часа, а 24 мин - это 0,2 часа. Таким образом, искомую вероятность можно вычислить по формуле:

Cтрока 52 (рис.2.8) содержит указанные расчеты. На рис.2.11. приведена иллюстрация для вычисления значений . Это площадь заштрихованной криволинейной трапеции и она равна 0,6826.

Аналогичные расчеты и диаграммы необходимо построить для двух других интервалов.

Рис.2.11 Использование графиков плотности и функции распределения экспоненциального распределения для вычисления искомой вероятности.

Задача 3:

Т.к. MS Excel не является специализированным математическим пакетом, в нем отсутствуют встроенные функции для построения плотности и функции распределения многих распределений. Поэтому для построения необходимо использовать функции, написанные пользователем UDF (user define function) написанные на встроенном языке VBA (Visual Basic for Application). Эти функции из [1] приведены в Приложении 1.

Для вычисления значений функций плотности распределений χ² (хи – квадрат), Стьюдента (t- распределение) и распределения Фишера (F -распределение) можно использовать UDF CPDF, TPDF и FPDF соответственно.

Распределение χ² (хи – квадрат)

Для нахождения критических значений р аспределения χ² в MS Excel имеется встроенная функция ХИ2ОБР ()

Синтаксис: ХИ2ОБР (p;df)

где

p — это p -значение;

df — это число степеней свободы.

Решение приведено на рис.2.12-2.17.

Рис.2.12.Построение таблицы значений функции плотности χ² при различном числе степеней свободы df (режим отображения данных)

Рис.2.13. Графики функции плотности χ² при различном числе степеней свободы df

Рис.2.14. Нахождение критических значений для различных p -значений распределения χ²

Рис.2.15. Геометрический смысл критических значений для различных p -значений

Рис.2.16. Построение таблицы значений функции плотности χ² при различном числе степеней свободы df (режим отображения формул)

Рис.2.17. Нахождение критических значений для различных p -значений распределения χ² (режим отображения формул)

Используя рис.2.13, сделайте вывод о симметричности распределения в зависимости от числа степеней свободы. Анализируя рис.2.14 -2.15, сделайте выводы об изменении критических значений в зависимости от p -значений.