КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ требуется строгое соблюдение указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены.
1. Каждая контрольная работа выполняется в тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 2 - 3 см для замечаний рецензента.
2. На обложке тетради должны быть ясно написаны фамилия и инициалы студента, группа, шифр, номер контрольной работы, название дисциплины и адрес студента. В конце работы ставится дата ее выполнения и подпись.
3. В работу включаются все задачи, указанные в задании, строго по положенному варианту.
4. Решения задач располагаются в порядке возрастания их номеров, указанных в задании, сохраняя номера задач.
5. Условия задач приводятся полностью. Решения излагаются подробно и аккуратно, объясняются все действия по ходу решения и делаются необходимые чертежи.
6. После получения прорецензированной работы, как незачтенной, так и зачтенной, исправляются отмеченные рецензентом ошибки и выполняются все рекомендации рецензента.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
К КОНТРОЛЬНОЙ РАБОТЕ № 1
1. Что называется определителем? Перечислить свойства определителей и методы их вычисления? Что такое минор и алгебраическое дополнение?
2. Запишите в общем виде систему линейных уравнений. Какая система называется однородной, неоднородной? Опишите метод Гаусса решения систем таких уравнений?
3. Напишите формулы Крамера. Когда применимы эти формулы?
4. Дайте определение геометрическим векторам, сложению и вычитанию векторов.
5. Как определяются скалярное, векторное и смешанное произведения векторов? Как эти произведения вычисляются через координаты векторов?
6. Напишите следующие уравнения плоскости: общее уравнение, нормальное уравнение, уравнение плоскости, проходящей через данную точку с заданной нормалью, уравнение плоскости в отрезках. Сформулируйте условия параллельности и перпендикулярности плоскостей?
7. Напишите общее уравнение прямой в пространстве, каноническое уравнение, уравнение прямой, проходящей через две точки. Сформулируйте условия параллельности и перпендикулярности прямых? Запишите условия параллельности и перпендикулярности прямой и плоскости, условие их пересечения.
8. Напишите следующие уравнения прямой на плоскости: уравнение прямой с угловым коэффициентом, общее уравнение прямой, нормальное уравнение. Как найти угол между прямыми? Сформулируйте условия параллельности и перпендикулярности прямых?
9. Дайте определение окружности, эллипса, гиперболы, параболы и напишите их канонические уравнения.
10. Начертите полярную систему координат и запишите формулы, связывающие прямоугольные и полярные координаты точки.
11. Дайте определение матрицы. Укажите, как они складываются, умножаются. Дайте определение обратной матрицы. Как найти обратную матрицу? Запишите систему линейных уравнений в матричной форме и объясните матричный метод ее решения.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
К КОНТРОЛЬНОЙ РАБОТЕ № 2
1. Дайте определение функции. Что называется областью определения функции? Что называется графиком функции? Какие функции называются четными, нечетными, периодическими и какие особенности их графиков?
2. Начертите графики основных элементарных функций.
3. Сформулируйте определение предела функции при стремлении аргумента к конечному пределу и при стремлении аргумента к бесконечности.
4. Как связано понятие предела функции с понятиями ее пределов слева и справа?
5. Какая функция называется бесконечно малой и какие ее основные свойства?
6. Какая функция называется бесконечно большой и как она связана с бесконечно малой?
7. Сформулируйте основные теоремы о пределах.
8. Что такое первый и второй замечательные пределы?
9. Сформулируйте определения непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции?
10. Сформулируйте определение производной. Каков ее механический и геометрический смысл?
11. Запишите формулы производных суммы, произведения, частного двух функций и таблицу производных.
12. Сформулируйте правило дифференцирования сложной функции и теорему о дифференцировании обратной функции.
13. Что такое логарифмическое дифференцирование?
14. Как находятся производные параметрически заданных функций?
15. Сформулируйте определение дифференциала функции. Каков его геометрический смысл?
16. В чем состоит правило Лопиталя для раскрытия неопределенностей?
17. Запишите формулу Тейлора с остаточным членом в форме Лагранжа в общем случае и для функций y=ex, y= sin x, y= cos x.
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Контрольная работа № 1
“Элементы аналитической геометрии и линейной алгебры”
Задача № 1
Даны координаты вершин пирамиды A1A2A3A4. Найти:
1) длину ребра A1A2;
2) угол между ребрами A1A2 и A1A4 ;
3) уравнение ребра A1A4, уравнение плоскости A1A2A3 и угол между ребром A1A4 и плоскостью A1A2A3;
4) уравнение высоты, опущенной из вершины A4 на грань A1A2A3;
5) площадь грани A1A2A3 и объем пирамиды;
6) показать, что векторы  ,
,  ,
,  , образуют базис и найти координаты вектора
, образуют базис и найти координаты вектора  в этом базисе.
в этом базисе.
| Номер варианта | A1 | A2 | A3 | A4 |
| 1 | (4;0;3) | (1;  3;2) 3;2)
| (2;  4;5) 4;5)
| ( 1;8;2) 1;8;2)
|
| 2 | (4;2;  3) 3)
| (2;1;0) | (1;2;  2) 2)
| (0;3;7) |
| 3 | (5;  2;4) 2;4)
| (2;0;4) | (2;1;  1) 1)
| (8;2;  1) 1)
|
| 4 | (0;2;7) | (2;3;1) | (3;2;4) | (2;  3;1) 3;1)
|
| 5 | (5;  1;0) 1;0)
| (3;2;2) | (2;  3;1) 3;1)
| (2;3;1) |
| 6 | (3;4;1) | (-2;5;3) | ( 2;5;0) 2;5;0)
| (3;2;  1) 1)
|
| 7 | ( 1;2;3) 1;2;3)
| (1;0;4) | ( 1;5;1) 1;5;1)
| (4;  2;3) 2;3)
|
| 8 | (4;  3;5) 3;5)
| (1;5;2) | (6;1;4) | (7;5;0) |
| 9 | (4;1;3) | ( 1;0;5) 1;0;5)
| (6;2;3) | (2;2;  3) 3)
|
| 10 | (1;3;  5) 5)
| (1;  2;1) 2;1)
| (0;  2;3) 2;3)
| (2;3;1) |
| 11 | (5;  3;4) 3;4)
| (2;3;  1) 1)
| (3;2;0) | ( 1;2;5) 1;2;5)
|
| 12 | (4;0;  3) 3)
| (1;4;  2) 2)
| (5;2;3) | (3;2;4) |
| 13 | (2;  1;2) 1;2)
| ( 1;4;0) 1;4;0)
| (2;1;3) | (3;4;  2) 2)
|
| 14 | ( 1;0;2) 1;0;2)
| (4;  4;1) 4;1)
| (2;6;3) | ( 2;5;4) 2;5;4)
|
| 15 | (2;  1;3) 1;3)
| ( 3;3;0) 3;3;0)
| (2;3;  1) 1)
| (1;2;  2) 2)
|
| 16 | (3;2;1) | (4;4;  1) 1)
| ( 5;0;4) 5;0;4)
| (3;1;4) |
| 17 | (1;2;  3) 3)
| (4;0;2) | ( 2;4;5) 2;4;5)
| (0;4;3) |
| 18 | (1;3;  3) 3)
| (2;4;2) | (6;  3;0) 3;0)
| (2;1;3) |
| 19 | (2;3;  4) 4)
| ( 4;1;3) 4;1;3)
| (4;  2;5) 2;5)
| (0;3;2) |
| 20 | (0;  2;5) 2;5)
| ( 4;2;3) 4;2;3)
| (2;3;1) | (3;4;0) |
Задача № 2
. Даны координаты вершин треугольника ABC. Найти:
1) уравнения сторон AB, BC и их угловые коэффициенты;
2) тангенс угла АBC;
3) уравнение высоты CD и ее длину;
4) уравнение медианы AE и координаты точки K пересечения этой медианы с высотой CD.
Сделать чертеж.
| Номер варианта | А | В | С |
| 1 | ( 4;2) 4;2)
| (4;  4) 4)
| (8;8) |
| 2 | (2;2) | ( 6; 6;  4) 4)
| ( 10;8) 10;8)
|
| 3 | ( 3,0) 3,0)
| (3;  6) 6)
| (9;6) |
| 4 | (6;4) | ( 2; 2;  2) 2)
| ( 6;10) 6;10)
|
| 5 | ( 3; 3;  1) 1)
| (3;5) | (9;  7) 7)
|
| 6 | (4;2) | ( 4; 4;  4) 4)
| ( 8;8) 8;8)
|
| 7 | (2;2) | ( 4; 4;  6) 6)
| (8;  10) 10)
|
| 8 | (3,0) | ( 3; 3;  6) 6)
| ( 9;6) 9;6)
|
| 9 | ( 6;4) 6;4)
| (2;  2) 2)
| (6;10) |
| 10 | (1;  3) 3)
| ( 5;3) 5;3)
| (7;9) |
| 11 | (2;  4) 4)
| ( 4; 4) 4; 4)
| (8;8) |
| 12 | ( 2;2) 2;2)
| (4;  6) 6)
| ( 8; 8;  10) 10)
|
| 13 | ( 3,0) 3,0)
| (3;6) | (9;  6) 6)
|
| 14 | (4;6) | ( 2; 2;  2) 2)
| (10;  6) 6)
|
| 15 | ( 1;-3) 1;-3)
| (5;3) | ( 7;9) 7;9)
|
| 16 | (2;4) | ( 4; 4;  4) 4)
| (8;  8) 8)
|
| 17 | (2;-2) | ( 6;4) 6;4)
| ( 10; 10;  8) 8)
|
| 18 | (0;  3) 3)
| ( 6;3) 6;3)
| (6;9) |
| 19 | (4;  6) 6)
| ( 2;2) 2;2)
| (10;6) |
| 20 | (3;  1) 1)
| ( 3;5) 3;5)
| ( 9; 9;  7) 7)
|
Задача № 3
Линия задана уравнением r = r (j) в полярной системе координат. Требуется:
1) построить линию по точкам от j =0 до j = p, придавая значения j через промежуток p /6;
2) найти уравнение линии в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось OX - с полярной осью;
3) определить вид линии по уравнению в декартовой системе координат;
4) сделать чертеж.
1. 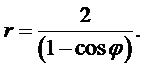 2.
2.  3.
3. 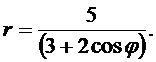 4.
4.  5.
5.  6.
6. 
7.  8.
8. 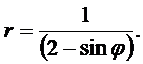 9.
9. 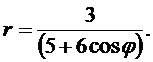 10.
10. 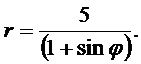 11.
11.  12.
12. 
13.  14.
14. 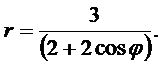 15.
15.  16.
16.  17.
17.  18.
18. 
19.  20.
20. 
Задача № 4
Сделать чертеж и составить уравнение линии:
1) расстояние каждой точки которой до точки А (3; 0) втрое меньше расстояния ее до прямой х =  1;
1;
2) каждая точка которой находится вдвое дальше от точки А (3;0), чем от точки В ( 3; 0);
3; 0);
3) расстояние каждой точки которой до точки А (2; 0) вдвое меньше расстояния до точки В (8; 0);
4) каждая точка которой равноудалена от точки А (1;2) и от оси ОY;
5) для каждой точки которой сумма квадратов расстояний до точек А (−2;0) и В (2;,0) равна 40;
6) для каждой точки которой сумма квадратов расстояний до осей координат и до прямых х =2 и y =2 равна 6;
7) расстояние каждой точки которой до точки А (4; 0) втрое меньше расстояния ее до прямой х =  4;
4;
8) каждая точка которой находится втрое дальше от точки А (3;0), чем от точки В ( 1; 0);
1; 0);
9) расстояние каждой точки которой до точки А (2; 0) втрое меньше расстояния до точки В ( 6; 0);
6; 0);
4) каждая точка которой равноудалена от точки А (2;3) и от оси ОX;
11) для каждой точки которой сумма квадратов расстояний до точек А (−3;0) и В (3;0) равна 68;
12) для каждой точки которой сумма квадратов расстояний до осей координат и до прямых х =4 и y =−4 равна 24;
13) расстояние каждой точки которой до точки А ( 2; 0) вдвое меньше расстояния ее до прямой х =4;
2; 0) вдвое меньше расстояния ее до прямой х =4;
14) каждая точка которой находится вдвое дальше от точки А ( 3; 0), чем от точки В (6; 0);
3; 0), чем от точки В (6; 0);
15) расстояние каждой точки которой до точки А (1; 0) вдвое меньше расстояния до точки В (4; 0);
16) каждая точка которой равноудалена от точки А (5;2) и от оси ОY;
17) для каждой точки которой сумма квадратов расстояний до точек А (−1;0) и В (1;0) равна 20;
18) для каждой точки которой сумма квадратов расстояний до осей координат и до прямых х =−2 и y =−2 равна 6;
19) расстояние каждой точки которой до точки А (1; 0) вдвое меньше расстояния ее до прямой х =  5;
5;
20) каждая точка которой находится втрое дальше от точки А ( 3;0), чем от точки В (5; 0).
3;0), чем от точки В (5; 0).
Задача № 5
Решить системы линейных уравнений: а) методом Гаусса, б) методом Крамера и используя обратную матрицу.
1. а)  б)
б)  .
.
2. а)  б)
б) 
3. а)  б)
б)  .
.
4. а)  б)
б) 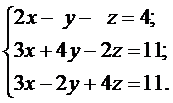
5. а)  б)
б) 
6. а)  б)
б) 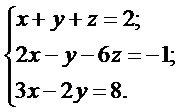
7. а)  б)
б) 
8. а)  б)
б) 
9. а) 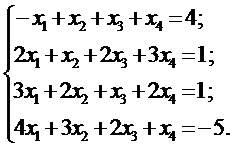 б)
б) 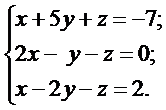
10. а)  б)
б) 
11. а)  б)
б) 
12. а)  б)
б) 
13. а)  б)
б) 
14. а)  б)
б) 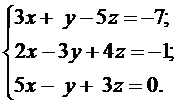
15. а) 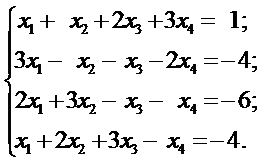 б)
б) 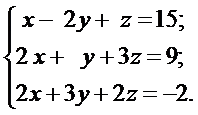
16. а)  б)
б) 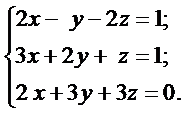
17. а)  б)
б) 
18. а)  б)
б) 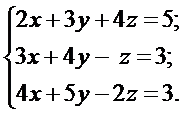
19. а) 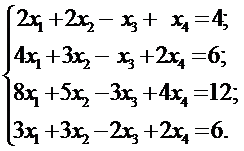 б)
б) 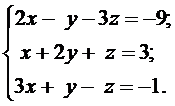
20. а)  б)
б) 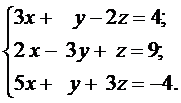
 2018-02-12
2018-02-12 251
251








