РАБОТЕ №2
Пример 1. Найти пределы, не пользуясь правилом Лопиталя:
а) 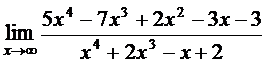 ; б)
; б) 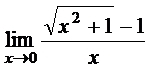 ;
;
в)  ; г)
; г) 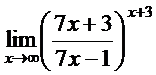 .
.
Решение. а) Знаменатель и числитель дроби стремятся к бесконечности при 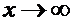 . Имеем неопределенность вида
. Имеем неопределенность вида 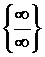 . Разделив числитель и знаменатель на x в наибольшей степени, т.е. на x 4, получим
. Разделив числитель и знаменатель на x в наибольшей степени, т.е. на x 4, получим
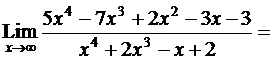
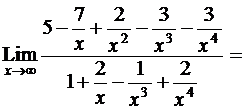 5,
5,
т.к. при 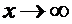 каждое из слагаемых в числителе и знаменателе кроме констант 5 и 1 стремится к нулю.
каждое из слагаемых в числителе и знаменателе кроме констант 5 и 1 стремится к нулю.
б) Для раскрытия неопределенности  при наличии иррациональной бесконечно малой величины в числителе необходимо избавиться от иррациональности, умножив числитель и знаменатель на сопряженное выражение, и сократить одинаковые бесконечно малые величины.
при наличии иррациональной бесконечно малой величины в числителе необходимо избавиться от иррациональности, умножив числитель и знаменатель на сопряженное выражение, и сократить одинаковые бесконечно малые величины.

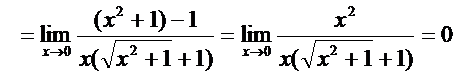 .
.
в) Воспользовавшись формулой тригонометрии 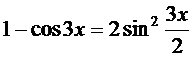 и первым замечательным пределом
и первым замечательным пределом  , имеем
, имеем

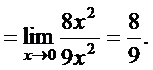
г) Для раскрытия неопределенности 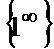 преобразуем дробь и показатель степени так, чтобы воспользоваться вторым замечательным пределом.
преобразуем дробь и показатель степени так, чтобы воспользоваться вторым замечательным пределом.
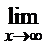
 =
= 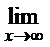
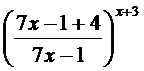 =
= 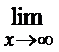
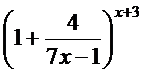 =
=
= 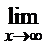
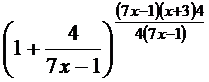 =
= 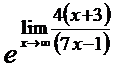 =
= 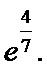
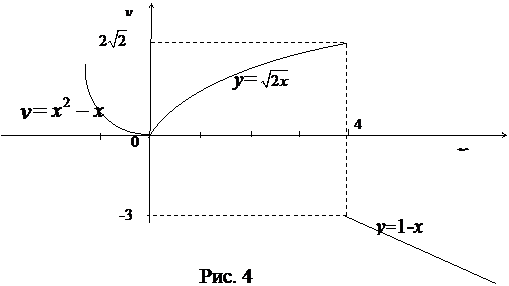
Пример 2. Задана функция 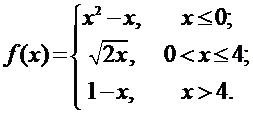 . Найти точки разрыва функции, если они существуют. Сделать чертеж.
. Найти точки разрыва функции, если они существуют. Сделать чертеж.
Решение. На промежутке (-∞,0) функция 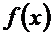 совпадает с функцией φ (х) =
совпадает с функцией φ (х) = 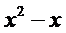 . Это элементарная функция, а элементарные функции непрерывны всюду, где они определены, Значит на промежутке
. Это элементарная функция, а элементарные функции непрерывны всюду, где они определены, Значит на промежутке
(-∞,0) функция φ (х) непрерывна, а, следовательно, непрерывна и функция 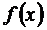 . Аналогично устанавливается непрерывность функции
. Аналогично устанавливается непрерывность функции 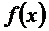 на промежутках (0,4), (4,∞).
на промежутках (0,4), (4,∞).
Исследуем непрерывность функции 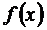 в точке
в точке  Для этого найдем правосторонний предел функции
Для этого найдем правосторонний предел функции 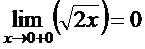 и левосторонний предел
и левосторонний предел  . Пределы совпадают и равны значению функции в этой точке. Функция
. Пределы совпадают и равны значению функции в этой точке. Функция 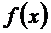 непрерывна в точке
непрерывна в точке 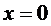 .
.
 |
Исследуем непрерывность функции 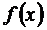 в точке
в точке 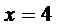 . Найдем правосторонний предел функции
. Найдем правосторонний предел функции 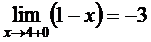 и левосторонний предел
и левосторонний предел 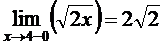 . Поскольку левосторонний и правосторонний пределы различными, оставаясь конечными, то
. Поскольку левосторонний и правосторонний пределы различными, оставаясь конечными, то 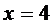 является точкой разрыва первого рода или скачком.
является точкой разрыва первого рода или скачком.
Сделаем чертеж
Пример 3. Найти производные 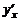 функций:
функций:
а)  ; б)
; б) 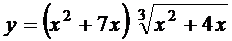 ;
;
в) 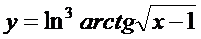 ; г)
; г) 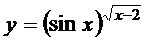 ;
;
д) 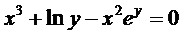 .
.
Решение. а) Пользуясь правилом дифференцирования сложной функции и таблицей производных, имеем
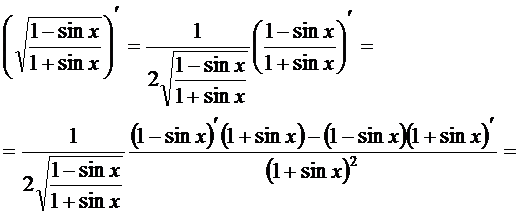

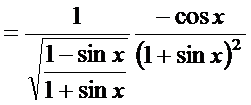 .
.
б) Имеем
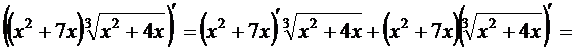
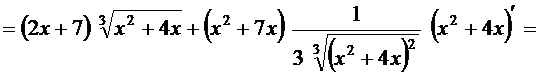
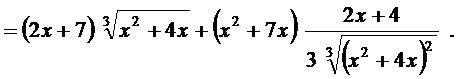
в) Имеем
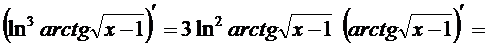
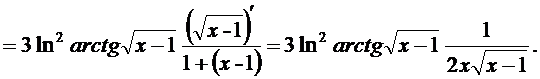
г) Прологарифмируем равенство 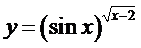 .
.
Имеем 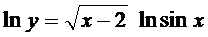 .
.
Продифференцируем обе части по 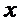 :
:
 ,
,
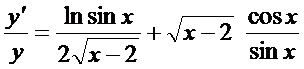 .
.
В результате имеем
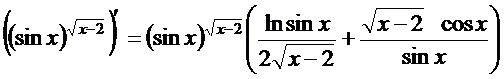 .
.
д) Уравнение 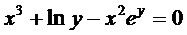 определяет у как неявную функцию от х. Дифференцируя обе части уравнения по х и учитывая, что у есть функция переменной х, получаем
определяет у как неявную функцию от х. Дифференцируя обе части уравнения по х и учитывая, что у есть функция переменной х, получаем
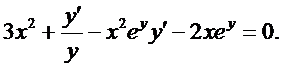
Из этого уравнения находим

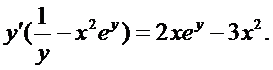

Пример 4. Найти производную второго порядка 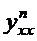 от функции, заданной параметрически.
от функции, заданной параметрически.

Решение. Если функция задана параметрически

то производные 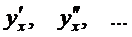 вычисляются по формулам
вычисляются по формулам
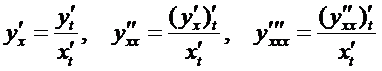 и т. д.
и т. д.
Найдем частные производные

Имеем
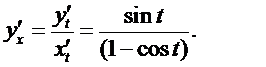
Продифференцируем полученное равенство по t
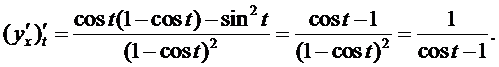
Окончательно получим

 2018-02-12
2018-02-12 216
216








