“Введение в анализ. Техника дифференцирования”
Задача № 1
Найти пределы, не пользуясь правилом Лопиталя.
1. а) 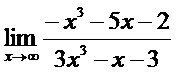 ; б)
; б) 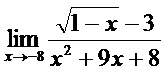 ;
;
в) 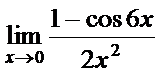 ; г)
; г) 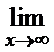
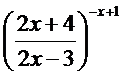 ;
;
2. а) 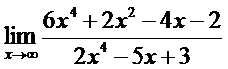 ; б)
; б) 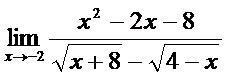 ;
;
в) 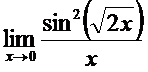 ; г)
; г) 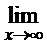
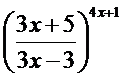 ;
;
3. а) 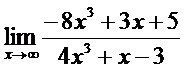 ; б)
; б) 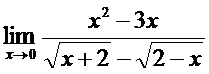 ;
;
в) 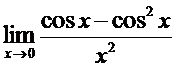 ; г)
; г) 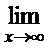
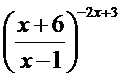 ;
;
4. а) 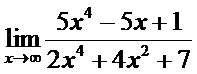 ; б)
; б) 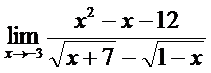 ;
;
в) 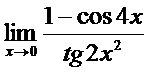 ; г)
; г) 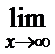
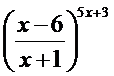 ;
;
5. а) 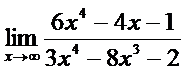 ; б)
; б) 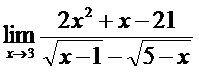 ;
;
в) 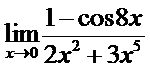 ; г)
; г) 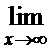
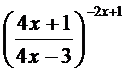 ;
;
6. а) 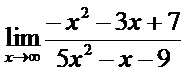
 ; б)
; б) 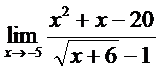 ;
;
в) 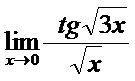 ; г)
; г) 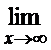
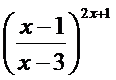 ;
;
7. а) 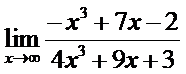 ; б)
; б) 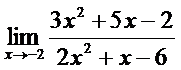 ;
;
в) 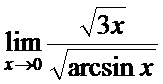 ; г)
; г) 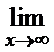
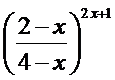 ;
;
8. а) 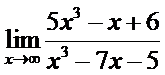 ; б)
; б) 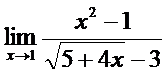 ;
;
в) 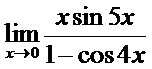 ; г)
; г) 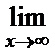
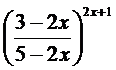 ;
;
9. а) 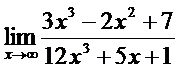 ; б)
; б) 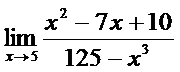 ;
;
в) 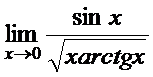 ; г)
; г) 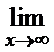
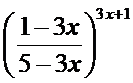 ;
;
10. а) 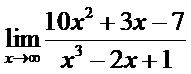 ; б)
; б) 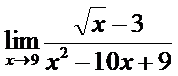 ;
;
в) 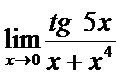 ; г)
; г) 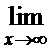
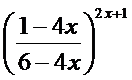 ;
;
11. а) 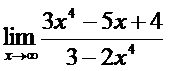 ; б)
; б) 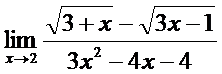 ;
;
в) 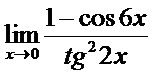 ; г)
; г) 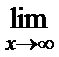
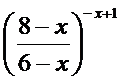 ;
;
12. а) 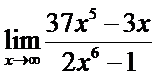 ; б)
; б) 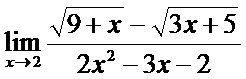 ;
;
в) 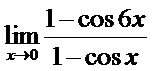 ; г)
; г) 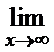
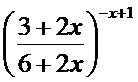 ;
;
13. а) 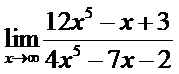 ; б)
; б) 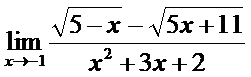 ;
;
в) 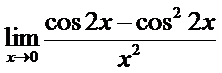 ; г)
; г) 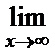
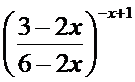 ;
;
14. а) 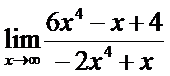 ; б)
; б) 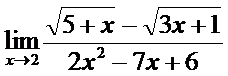 ;
;
в) 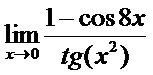 ; г)
; г) 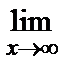
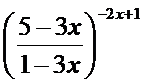 ;
;
15. а) 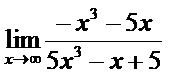 ; б)
; б) 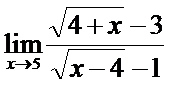 ;
;
в) 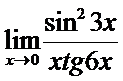 ; г)
; г) 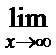
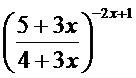 ;
;
16. а) 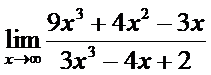 ; б)
; б) 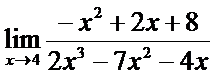 ;
;
в) 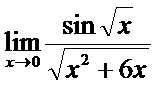 ; г)
; г) 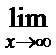
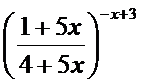 ;
;
17. а) 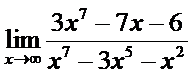 ; б)
; б) 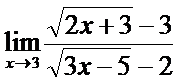 ;
;
в) 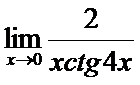 ; г)
; г) 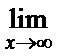
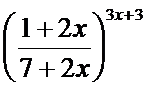 ;
;
18. а) 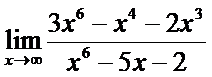 ; б)
; б) 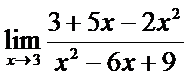 ;
;
в) 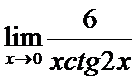 ; г)
; г) 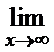
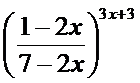 ;
;
19. а) 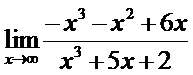 ; б)
; б) 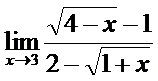 ;
;
в) 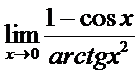 ; г)
; г) 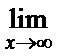
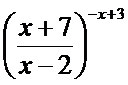 ;
;
20. а) 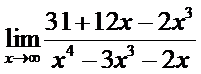 ; б)
; б) 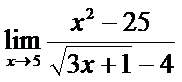 ;
;
в) 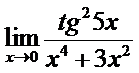 ; г)
; г) 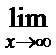
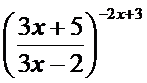 ;
;
Задача № 2
Задана функция f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
1. 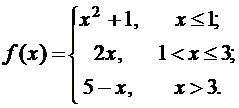 2.
2. 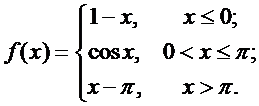
3. 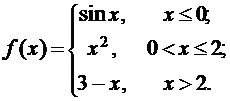 4.
4. 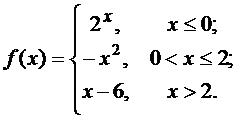
5. 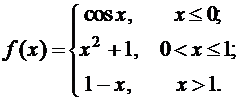 6.
6. 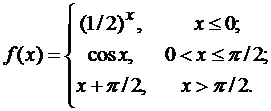
7. 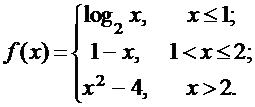 8.
8. 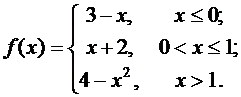
9. 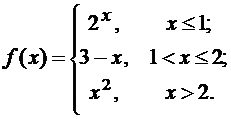 10.
10. 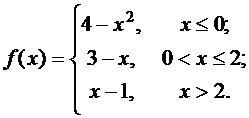
11. 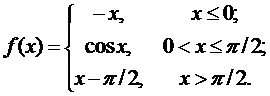 12.
12. 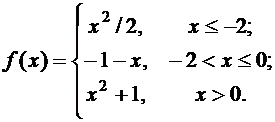
13. 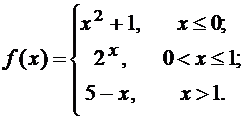 14.
14. 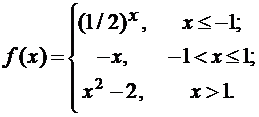
15. 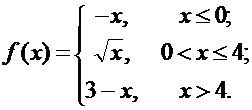 16.
16. 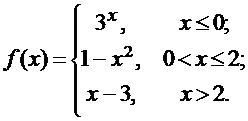
17. 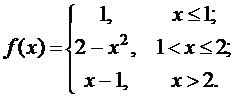 18.
18. 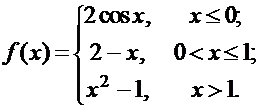
19. 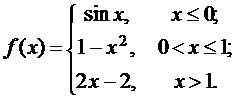 20.
20. 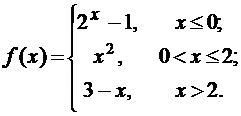
Задача № 3
Найти производные 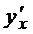 функций.
функций.
1. а) 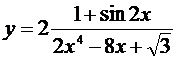 ; б)
; б) 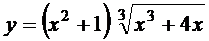 ;
;
в) 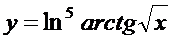 ; г)
; г) 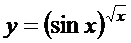 ,
,
д) x tg y = y sin x.
2. а) 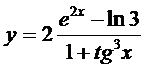 ; б)
; б) 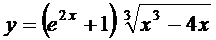 ;
;
в)  ; г)
; г) 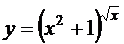 ;
;
д) (sin x) /y = (cos y) /x.
3. а) 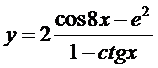 ; б)
; б) 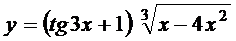 ;
;
в) 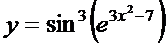 ; г)
; г) 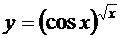 ;
;
д) (x+y) sin x = cos y.
4. а) 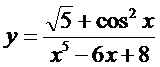 ; б)
; б) 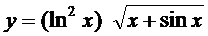 ;
;
в) 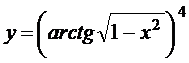 ; г)
; г) 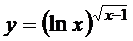 ;
;
д) x sin (x+y) = y.
5. а) 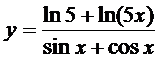 ; б)
; б) 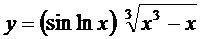 ;
;
в) 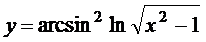 ; г)
; г) 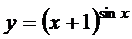 ;
;
д) y/x = sin (x 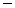 y).
y).
6. а) 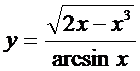 ; б)
; б) 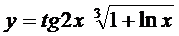 ;
;
в) 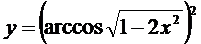 ; г)
; г) 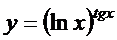 ;
;
д) xy = sin (x+y).
7. а) 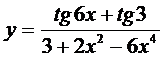 ; б)
; б) 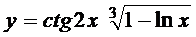 ;
;
в) 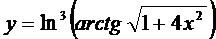 ; г)
; г) 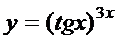 ;
;
д) x/y = ctg (x+y).
8. а) 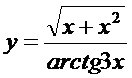 ; б)
; б) 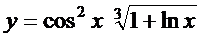 ;
;
в) 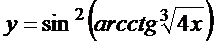 ; г)
; г) 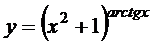 ;
;
д) x cos y 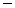 y sin x = 0.
y sin x = 0.
9. а) 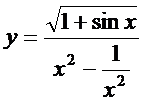 ; б)
; б) 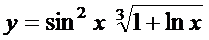 ;
;
в) 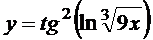 ; г)
; г) 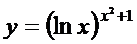 ;
;
д) 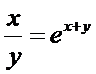 .
.
10. а) 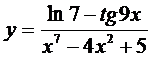 ; б)
; б) 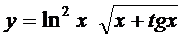 ;
;
в) 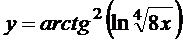 ; г)
; г) 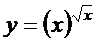 ;
;
д) 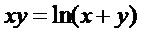 .
.
11. а) 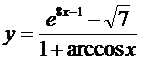 ; б)
; б) 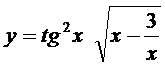 ;
;
в) 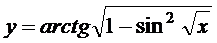 ; г)
; г)  ;
;
д) 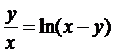 .
.
12. а) 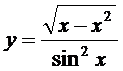 ; б)
; б) 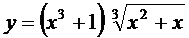 ;
;
в) 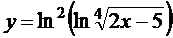 ; г)
; г) 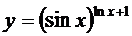 ;
;
д) 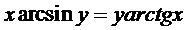 .
.
13. а) 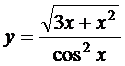 ; б)
; б) 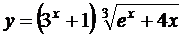 ;
;
в) 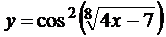 ; г)
; г) 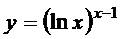 ;
;
д) 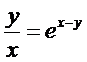 .
.
14. а) 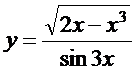 ; б)
; б) 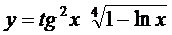 ;
;
в) 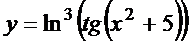 ; г)
; г) 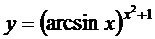 ;
;
д) 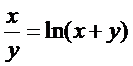 .
.
15. а) 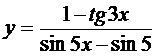 ; б)
; б) 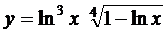 ;
;
в) 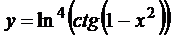 ; г)
; г) 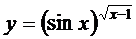 ;
;
д) 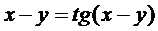 .
.
16. а) 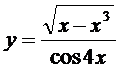 ; б)
; б) 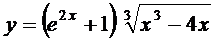 ;
;
в) 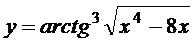 ; г)
; г) 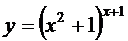 ;
;
д) cos(x-y)= x +2 y.
17. а) 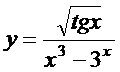 ; б)
; б) 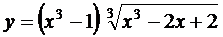 ;
;
в) 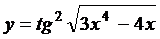 ; г)
; г) 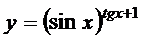 ;
;
д) 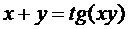 .
.
18. а) 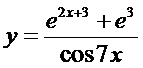 ; б)
; б) 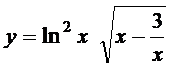 ;
;
в) 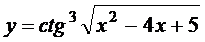 ; г)
; г) 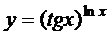 ;
;
д) 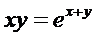 .
.
19. а) 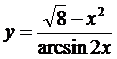 ; б)
; б) 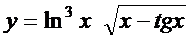 ;
;
в) 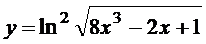 ; г)
; г) 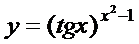 ;
;
д) 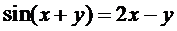 .
.
20. а) 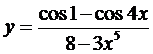 ; б)
; б) 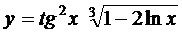 ;
;
в) 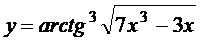 ; г)
; г) 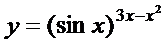 ;
;
д) 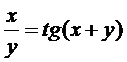 .
.
Задача 4
Найти производную второго порядка 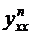 от функции, заданной параметрически.
от функции, заданной параметрически.
1. 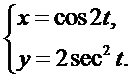 2.
2. 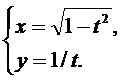 3.
3. 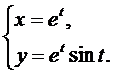
4. 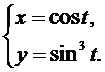 5.
5. 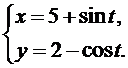 6.
6. 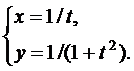
7. 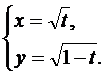 8.
8. 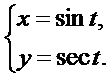 9.
9. 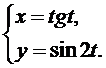
10. 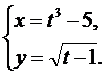 11.
11. 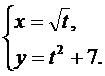 12.
12. 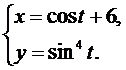
13. 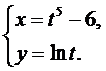 14.
14. 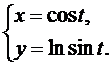 15.
15. 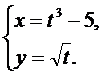
16. 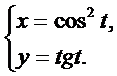 17.
17. 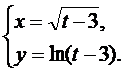 18.
18. 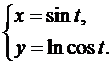
19. 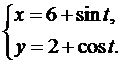 20.
20. 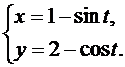
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КОНТРОЛЬНОЙ
РАБОТЕ № 1
Пример 1. Даны координаты вершин пирамиды 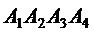 :
: 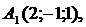
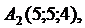
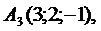
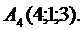 Найти:
Найти:
1) длину ребра 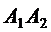 ;
;
2) угол между ребрами 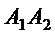 и
и 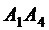 ;
;
3) уравнение ребра 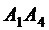 , уравнение плоскости
, уравнение плоскости 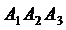 и угол между ребром
и угол между ребром 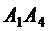 и плоскостью
и плоскостью 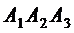 ;
;
4) уравнение высоты, опущенной из вершины 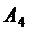 на грань
на грань 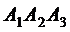 и ее длину;
и ее длину;
5) площадь грани 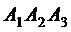 и объем пирамиды;
и объем пирамиды;
6) показать, что векторы 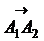 ,
, 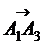 ,
, 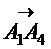 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 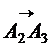 в этом базисе.
в этом базисе.
Решение. Найдем координаты векторов, которые совпадают с выходящими из вершины 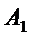 ребрами пирамиды:
ребрами пирамиды: 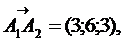
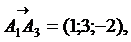
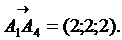
1) Длина ребра 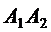 совпадает с расстоянием между точками
совпадает с расстоянием между точками 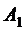 и
и 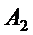 :
:
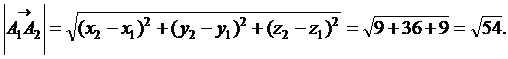
2) Определим угол между векторами, используя скалярное произведение. Так как 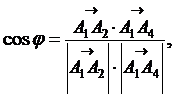 то
то
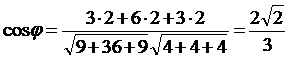 ,
, 
3) Уравнение прямой, проходящей через две точки, имеет вид
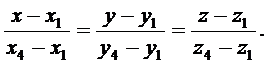
Подставляя в уравнение координаты точек A1 и A4, получим
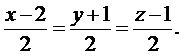
Уравнение плоскости, проходящей через три заданные точки, имеет вид
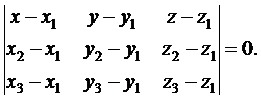
Подставляя в уравнение координаты точек 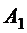 ,
, 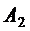 и
и 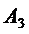 , получим
, получим
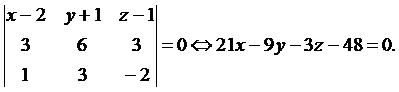
Синус угла между прямой 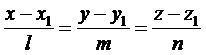 и плоскостью
и плоскостью 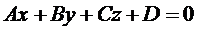 определяется по формуле
определяется по формуле
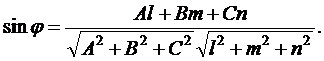
Используя эту формулу, находим
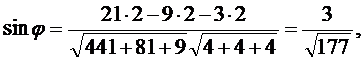
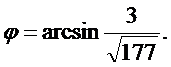
4) Уравнение высоты найдем как уравнение прямой, проходящей через точку 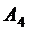 перпендикулярно плоскости
перпендикулярно плоскости 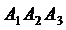 , задаваемой уравнением
, задаваемой уравнением 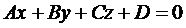 . В качестве направляющего вектора прямой может быть взят вектор нормали плоскости
. В качестве направляющего вектора прямой может быть взят вектор нормали плоскости 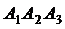 . Уравнение высоты имеет вид
. Уравнение высоты имеет вид
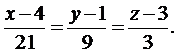
Для нахождения длины высоты можно использовать формулу 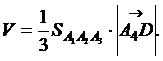 Объем V и площадь
Объем V и площадь 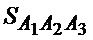 будут найдены в п. 5). Поэтому
будут найдены в п. 5). Поэтому
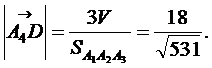
5) Площадь треугольника равна половине площади параллелограмма, построенного на векторах 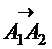 и
и 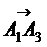 . Найдем вначале векторное произведение этих векторов. Имеем
. Найдем вначале векторное произведение этих векторов. Имеем
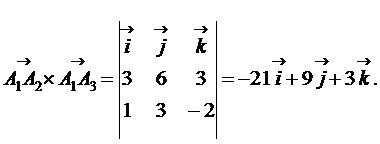
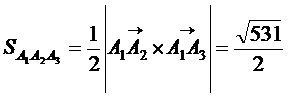 .
.
Объем пирамиды равен 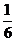 части объема параллелепипеда, построенного на данных векторах, поэтому вначале находим смешанное произведение этих векторов. Имеем
части объема параллелепипеда, построенного на данных векторах, поэтому вначале находим смешанное произведение этих векторов. Имеем
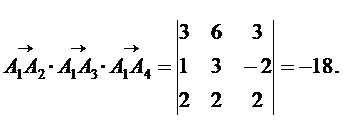
Поэтому 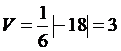 .
.
6) Для того, чтобы векторы 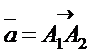 , `
, ` 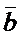
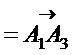 , `
, ` 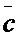
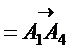 образовывали базис, необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля. В п. 5) мы уже вычислили смешанное произведение ` a
образовывали базис, необходимо и достаточно, чтобы их смешанное произведение было отлично от нуля. В п. 5) мы уже вычислили смешанное произведение ` a 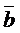
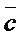 = – 18 ¹ 0.
= – 18 ¹ 0.
Таким образом, эти векторы образуют базис. Найдем координаты вектора 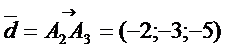 в базисе` a,
в базисе` a, 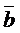 ,
, 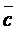 . Обозначим эти координаты x, y, z. Тогда имеем равенство
. Обозначим эти координаты x, y, z. Тогда имеем равенство 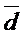 = x a + y
= x a + y 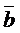 + z
+ z 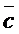 , которое в координатной форме примет вид системы уравнений относительно неизвестных x, y, z
, которое в координатной форме примет вид системы уравнений относительно неизвестных x, y, z
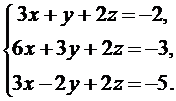
Решим систему уравнений методом Крамера. Определитель этой системы 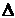 =
=  18. Вспомогательные определители:
18. Вспомогательные определители:
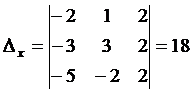 ,
, 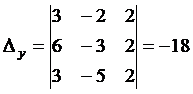 ,
,
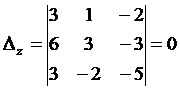 .
.
Решение системы уравнений получим по формулам Крамера
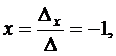
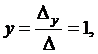
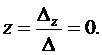
Итак, вектор 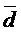 в базисе ` a,
в базисе ` a, 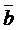 ,
, 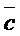 имеет координаты (
имеет координаты ( 1;1;0).
1;1;0).
Пример 2. Даны координаты вершин треугольника 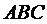 :
: 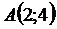 ,
, 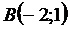 ,
, 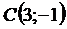 . Найти:
. Найти:
1) уравнения сторон 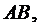
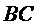 и их угловые коэффициенты;
и их угловые коэффициенты;
2) угол 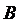 в радианах или градусах с точностью до двух знаков;
в радианах или градусах с точностью до двух знаков;
3) уравнение высоты 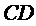 и ее длину;
и ее длину;
4) уравнение медианы 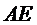 и координаты точки
и координаты точки 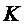 пересечения этой медианы с высотой
пересечения этой медианы с высотой 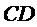 .
.
Сделать чертеж.
Решение. Найдем координаты векторов 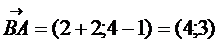 и
и 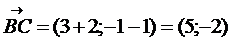 .
.
1) Уравнение стороны 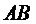 получим как уравнение прямой, проходящей через две заданные точки
получим как уравнение прямой, проходящей через две заданные точки 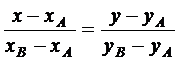 . Подставляя в уравнение координаты точек A и В, имеем
. Подставляя в уравнение координаты точек A и В, имеем
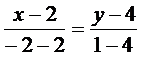 ,
, 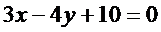 ,
, 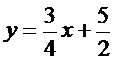 .
.
Угловой коэффициент прямой 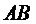 равен
равен 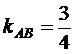 . Аналогичным образом находим уравнение стороны
. Аналогичным образом находим уравнение стороны 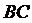 :
:
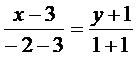 ,
, 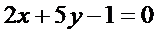 ,
, 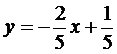 .
.
Угловой коэффициент прямой 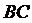 равен
равен 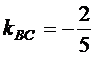 .
.
2) Определим угол 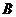 между векторами
между векторами 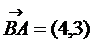 и
и 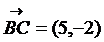 , используя скалярное произведение. Так как
, используя скалярное произведение. Так как 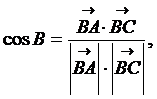 то
то
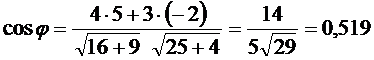 ,
, 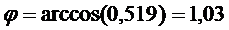 .
.
3) Уравнение высоты 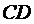 находится как уравнение прямой, проходящей через точку
находится как уравнение прямой, проходящей через точку 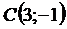 перпендикулярно вектору
перпендикулярно вектору 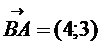 . Имеем
. Имеем 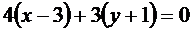 или
или 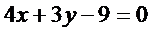 . Длина высоты
. Длина высоты 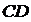 вычисляется как расстояние от точки
вычисляется как расстояние от точки 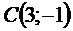 до прямой
до прямой 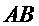 :
:
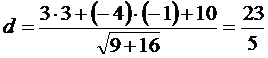 .
.
4) Находим координаты середины отрезка 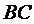 :
:
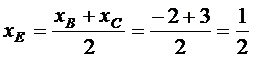 ,
, 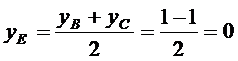 .
.
Уравнение медианы  получается как уравнение прямой линии, проходящей через две точки
получается как уравнение прямой линии, проходящей через две точки 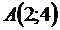 и
и 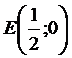 . Имеем
. Имеем
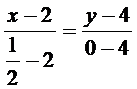 ,
, 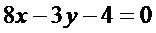 .
.
Координаты точки 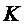 пересечения прямых
пересечения прямых 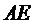 и
и 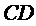 находятся из системы уравнений этих прямых
находятся из системы уравнений этих прямых
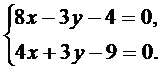
Вычисления дают 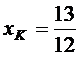 ,
, 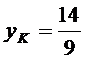 .
.
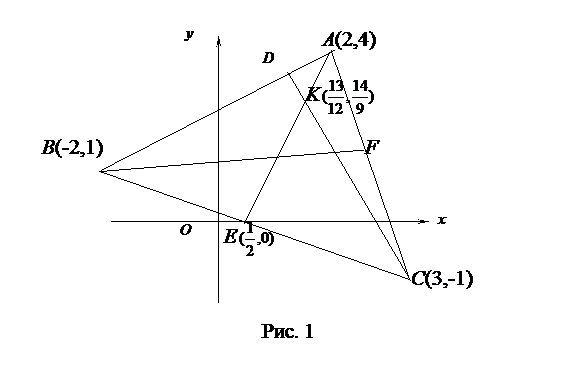
Пример 3. Найдите уравнение линии 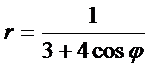 в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось OX - с полярной осью. Определите вид линии по уравнению в декартовой системе координат.
в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось OX - с полярной осью. Определите вид линии по уравнению в декартовой системе координат.
Решение. Воспользуемся формулами, связывающими координаты точки в декартовой и полярной системе координат: 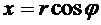 ,
, 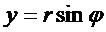 ,
, 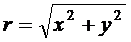 ,
, 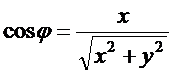 ,
, 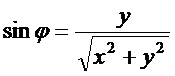 .
.
Получим
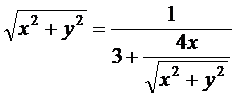 ,
,
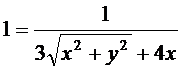 ,
, 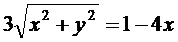 .
.
Возведение в квадрат обеих частей приводит к равенству
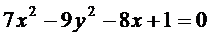 .
.
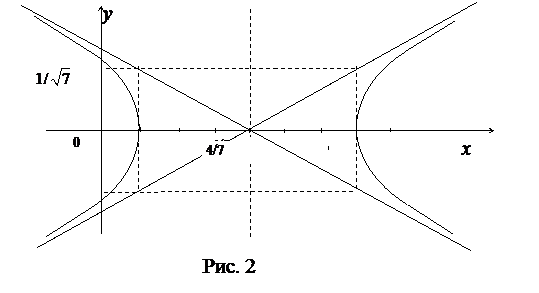
Выделяя полный квадрат, получим
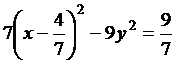 .
.
Разделив обе части уравнения на 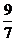 , убеждаемся, что искомая кривая является гиперболой
, убеждаемся, что искомая кривая является гиперболой
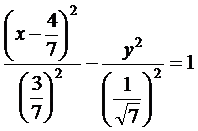 ,
,
смещенной вдоль оси OX на 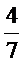 вправо.
вправо.
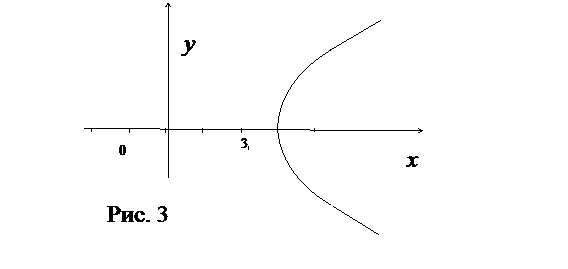
Пример 4 Составить уравнение линии,каждая точка которой одинаково удалена от прямой х = 2 и от точки А (4;0). Сделать чертеж.
Решение. Пусть точка М (х;у) принадлежит искомой линии. Расстояние между точками 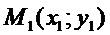 и
и 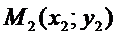 вычисляется по формуле
вычисляется по формуле
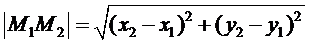 .
.
По условию задачи 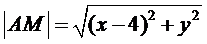 .
.
Расстояние от точки 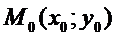 до прямой, заданной уравнением
до прямой, заданной уравнением 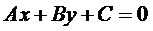 , вычисляется по формуле
, вычисляется по формуле
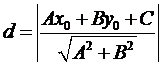 .
.
Уравнение прямой х – 2 =0. Следовательно 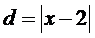 . По условию задачи d=
. По условию задачи d= 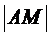 . Поэтому
. Поэтому
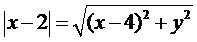 .
.
Возведем обе части уравнения в квадрат. Приводя подобные, получим 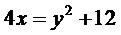 или
или 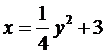 . Следовательно, искомая линия является параболой.
. Следовательно, искомая линия является параболой.
Пример 5. Решить систему линейных уравнений по формулам Крамера и используя обратную матрицу
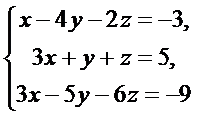
Решение. Вычислим определитель системы
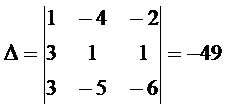 .
.
Определитель отличен от нуля. Следовательно, система имеет единственное решение
1)Решая систему уравнений методом Крамера, вычислим дополнительные определители:
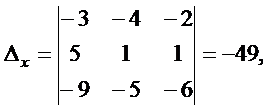
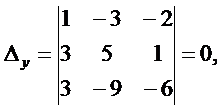
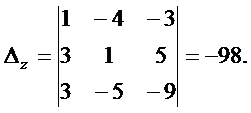
По формулам Крамера получим решение системы уравнений: 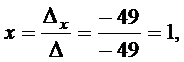
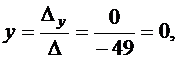
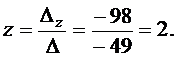
2) Так как определитель не равен нулю, то матрица системы является невырожденной и, следовательно, имеет обратную матрицу. Запишем исходную систему уравнений в матричном виде
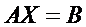
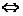
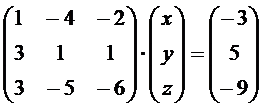 .
.
Умножив обе части этого уравнения слева на матрицу A- 1, получим X= A- 1 B. Здесь A- 1 матрица обратная А, которая находится по формуле
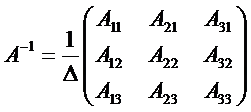
Для построения обратной матрицы найдем алгебраические дополнения к элементам матрицы A. Имеем
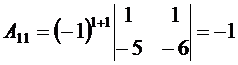 ,
, 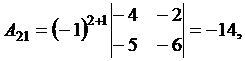
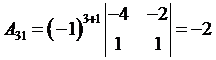 ,
, 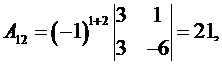
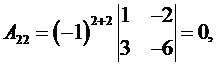
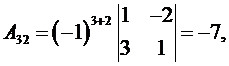
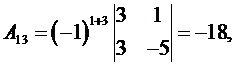
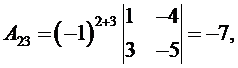
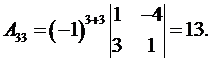
Обратная матрица A -1 имеет вид
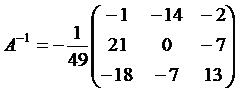 ,
, 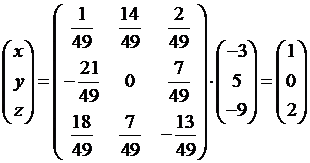 .
.
Следовательно, 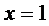 ,
, 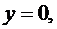
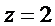 .
.
Пример 6. Решить систему уравнений методом Гаусса
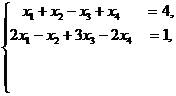
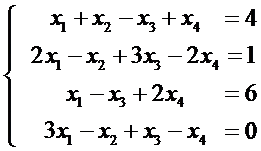
Решение. В соответствие с методом Гаусса запишем расширенную матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов
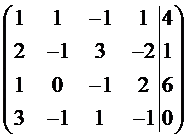
С помощью элементарных преобразований из расширенной матрицы системы получим треугольную матрицу. Умножим первую строку на -2 и прибавим ее ко второй. Умножим первую строку на -1 и прибавим ее к третьей. Умножим первую строку на -3 и прибавим ее к четвертой. Получим
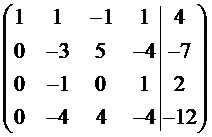
 .
.
Поменяем местами вторую и третью строки. Четвертую строку разделим на 4. Получим
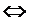
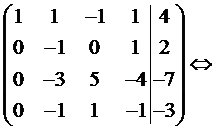
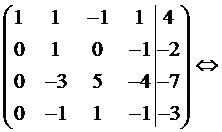
Умножив полученную вторую строку на 3, прибавим ее к третьей строке; прибавим вторую строку к четвертой. Получим
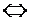

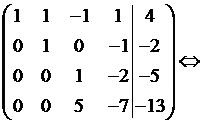
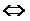
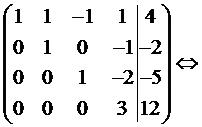
Таким образом, основная матрица приведена к «треугольному виду». Система имеет единственное решение.
Запишем систему в явном виде
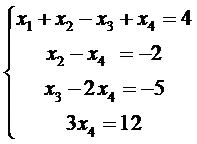
Осуществляя обратный ход от последнего уравнения к первому, получаем решение системы: 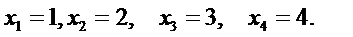
 2018-02-12
2018-02-12 352
352








