2018-02-20
267
Пусть функция f (х) непрерывна но отрезке [ a; b ] и дифференцируема во всех внутренних точках этого отрезка, за исключением, быть может, конечного числа точек. Пусть, кроме того, функция f (х) имеет на отрезке [ a; b ] конечное число стационарных точек.
Так как функция f (х) непрерывна на отрезке [ a; b ], то по второй теореме Вейерштрасса она достигает наибольшего и наименьшего значений в некоторых точках этого отрезка. Эти точки могут быть либо концами отрезка [ a; b ], либо внутренними точками этого отрезка.
Если функция f (х) принимает наибольшее (наименьшее) значение в некоторой внутренней точке С отрезка [ a; b ], то f (С) будет совпадать с локальным максимумом (минимумом).
Пример Приведем графическую иллюстрацию некоторых возможных случаев
 |
M M
m m M M m M m m
a b a b a b a b a b
Здесь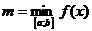 
, 
.
|
|
|
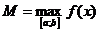Из сказанного следует правило отыскания наибольшего и наименьшего значения функций на отрезке:
1. Найти все критические точки функции f (х), лежащие внутри отрезка [ a; b ].
2. Найти значения функции в этих точках на концах отрезка [ a; b ] (f (a) и f (b)).
3. Выбрать из полученных значений функции f (х) наибольшее и наименьшее значения.
Пример Найти наибольшее и наименьшее значения функции у = х 4 – 2 х 2 +1 на отрезке [–2;2].
1. Критические точки (см. пример выше): х =0; х =1; х =-1. Все они принадлежат отрезку [–2;2].
2. f (0) = 1; f (1) = f (–1) = 0, f (2) = f (–2) = 16 – 8 + 1 = 9. 3.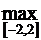 
f (х) = 9; 
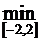f (х) = 0.
