Применение дифференциального исчисления к исследованию функций
Условие монотонности функции на числовом промежутке
Теорема 1 Необ х одимое и достаточное условие невозрастания (неубывания) функции на числовом промежутке
Пусть функция f (х) непрерывна на числовом промежутке Х , тогда, для того, чтобы функция f (х) была невозрастающей (неубувающей) на промежутке Х, необходимо и достаточно, чтобы  (
( )
)
для всех внутренних точек этого промежутка.
Замечание Аналогично можно доказать условие постоянства функции на числовом промежутке Х, которое заключается в равенстве нулю ее производной для " х Î Х, т.е.  .
.
Теорема 2 Достаточное условие возрастания (убывания) функции. Если функция f (х) непрерывна на числовом промежутке Х и имеет положительную (отрицательную) производную во всех внутренних точках этого промежутка, за исключением конечного числа точек, в которых конечная производная не существует или конечная производная равна нулю, то функция f (х) возрастает (убывает) на промежутке Х.
Доказательство этого утверждения состоит из двух этапов:
1) устанавливается возрастание функции f (х) на каждом из промежутков, на которые делится промежуток Х указанными в теореме точками (где  не существует, либо равна нулю);
не существует, либо равна нулю);
2) в силу непрерывности функции f (х) на промежутке Х устанавливается ее возрастание (убывание) на всем промежутке Х.
| Пример |
0 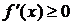
|  (не убывает)
(не убывает)
|

|  (не возрастает)
(не возрастает)
| |

|
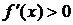
|  (возрастает)
(возрастает)
|
| существует при " х Î Х |

|  (убывает)
(убывает)
|
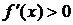 и и
 - у конечного числа точек - у конечного числа точек
|  (возрастает)
(возрастает)
| |

 - у конечного числа точек - у конечного числа точек
|  (убывает)
(убывает)
| |
 Не существует
Не существует
| 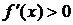
| 
 (возрастает) (возрастает)
|
| у конечного числа точек | 
| (убывает) |
Необходимое и достаточное условие экстремума функции в точке
Определение Точка х 0 из D (f) называется точкой строгого локального максимума (минимума) функции f (х), если для всех х из некоторой d – окрестности U (х 0,d) точки х 0, х ¹ х 0, выполняется неравенство
f (х) < f (х 0) [ f (х) > f (х 0)] (1)
Точки локального максимума и локального минимума называются точками локального экстремума.
Значения функций в этих точках называются соответственно локальным максимумом или локальным минимумом (локальными экстремумами функции).
 Из определения следует, что понятие экстремума носит локальный характер в том смысле, что в случае экстремума неравенство (1) не обязательно выполняется для всех х Î D (f), а лишь в некоторой окрестности U (х 0,d) точки х 0.
Из определения следует, что понятие экстремума носит локальный характер в том смысле, что в случае экстремума неравенство (1) не обязательно выполняется для всех х Î D (f), а лишь в некоторой окрестности U (х 0,d) точки х 0.
Т.о., функция может иметь несколько локальных максимумов (минимумов), причем может оказаться, что локальный максимум меньше, чем локальный минимум.
 |
У лок. max
лок. max лок. min
лок. min
О х
Теорема 1 Необходимое условие существование экстремума Если функция определена в некоторой окрестности точки х 0 и имеет в ней локальный экстремум, тогда эта функция
1) либо дифференцируема в точке х 0 и 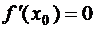 ,
,
2) либо недифференцируема в точке х 0.
Пример В точке х 0= 0 функция  недифференцирума, но имеет локальный минимум.
недифференцирума, но имеет локальный минимум.
Замечание Условия теоремы 1 являются лишь необходимыми условиями существования экстремума.
Следствие Из теоремы 1 вытекает, что точки локального экстремума функции следует искать среди корней уравнения  и точек, где производная не существует.
и точек, где производная не существует.
Точки, в которых производная не существует или равна нулю называются критическими точками первого рода или точками подозрительными на экстремум.
Точки, для которых выполняется условие  , называются стационарными.
, называются стационарными.
Пример1. Для функции y 1= х 3
 при х =0,
но в этой точке данная функция экстремума не имеет. при х =0,
но в этой точке данная функция экстремума не имеет.
|
 у y 1= х 3 у y 1= х 3
 О х О х
|
2. Для функции  производная производная 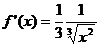 не существует при х = 0, но в этой точке экстремума нет.
не существует при х = 0, но в этой точке экстремума нет.
| 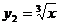 х
х
|
 2018-02-20
2018-02-20 1385
1385