Пусть функция y = f (х) определена на числовом промежутке (a; b) и х 1 и х 2 – любые фиксированные точки этого промежутка, причем х 1< х 2. Тогда уравнение прямой, проходящей через точки М 1(х 1; y 1) и М 2(х 2; y 2) имеет вид 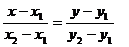 или
или  . (1)
. (1)
Для простоты обозначим первую часть уравнения (1) через l (х), тогда y = l (х).

 у y = l (х) у
у y = l (х) у
f (х) М 2
l (х) М 1
М 1 l (х) М 2
f (х)
y = l (х)
О а х1 х х2 b x О а х1 х х2 b x
Определение 1 Функция f (х) называется выпуклой вверх (вниз) на числовом промежутке (a; b), если каковы бы ни были точки х 1 и х 2 (х 1< х 2) из этого промежутка, для " х Î(х 1, х 2) выполняется неравенство
f (х) ³ l (х) [ f (х) £ l (х)].
Если к тому же это неравенство строгое, то функция f (х) называется строго выпуклой вверх (вниз) на промежутке (a; b).
Геометрически это определение означает, что функция f (х) называется выпуклой вверх (вниз) на промежутке (a; b), если каждая дуга ее графика на этом промежутке лежит не ниже (не выше) стягивающей ее хорды.
Теорема 1 Пусть функция f (х) дважды дифференцируема в каждой точке промежутка Х, тогда если для " х Î Х выполняется условие  (
( ), то функция f (х) выпукла вниз (вверх) на промежутке Х.
), то функция f (х) выпукла вниз (вверх) на промежутке Х.
 Замечание Условие теоремы (1) не является необходимым условием строгой выпуклости функции.
Замечание Условие теоремы (1) не является необходимым условием строгой выпуклости функции.
Пример Функция
у = х 4
строго выпукла, хотя
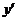 = 4 х 3, = 4 х 3,
 = 12 х 2, = 12 х 2,  (0) = 0. (0) = 0.
| у у = х 4 О х |
Опрределение 2 Пусть функция f (х) непрерывна в точке a. Точка a называется точкой перегиба функции f, если она одновременно является концом промежутка выпуклости вверх и концом промежутка выпуклости вниз функции f (х).
 При этом точка (a; f (a)) называется точкой перегиба графика функции f (х).
При этом точка (a; f (a)) называется точкой перегиба графика функции f (х).
Теорема 2 Пусть точка а является точкой перегиба функции f (х) и функция f (х) дважды дифференцируема в этой точке, тогда
 . .
| у f (a) О а х |
Замечание Функция f (х), имеющая в точке а перегиб, может быть и не дифференцируемой дважды в этой точке.
 Пример у
Пример у
Функция  не имеет в точке х = 0 конечной второй производной, однако точка х 0 = 0 – точка перегиба. не имеет в точке х = 0 конечной второй производной, однако точка х 0 = 0 – точка перегиба.
|  х
х
|
Т.о. к точкам перегибам могут относиться точки, в которых функция f (х) непрерывна и 1) либо 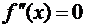 , либо
, либо  – не существует.
– не существует.
Точки, удовлетворяющие указанным условиям, называются критическими точками второго рода или точками подозрительные на перегиб.
Не каждая критическая точка второго рода является точкой перегиба. Для того, чтобы судить, будет ли критическая точка второго рода точкой перегиба, следует обратиться к достаточному признаку точек перегиба.
Теорема 3 Достаточный признак точки перегиба Пусть функция f (х) непрерывна и дважды дифференцируема в некоторой окрестности U (a;d) точки а, за исключением, быть может, самой точки а, тогда, если функция  имеет разное значение на промежутках (a – d; a) и (а; a + d), то а – точка перегиба функции f (х). Если же на этих промежутках функция
имеет разное значение на промежутках (a – d; a) и (а; a + d), то а – точка перегиба функции f (х). Если же на этих промежутках функция  имеет одинаковые знаки, то а – не является точкой перегиба функции f (х).
имеет одинаковые знаки, то а – не является точкой перегиба функции f (х).
Справедливость теоремы непосредственно следует из теоремы 1 и определения точки перегиба.
Пример Исследовать на перегиб функцию 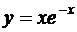 .
.
1) D (f)= R. 2) 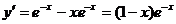
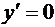 при х = 1 (стационарная точка).
при х = 1 (стационарная точка).
3) 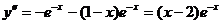 .
.  при х = 2, следовательно, х = 2 – критическая точка второго рода. Результаты исследований оформим в виде таблицы
при х = 2, следовательно, х = 2 – критическая точка второго рода. Результаты исследований оформим в виде таблицы
| х | (–¥;2) | 2 | (2;+¥) |

| – | 0 | + |

| 
| 2/e2 точка перегиба |

 Т.о., точка
Т.о., точка  ) – точка перегиба данной функции.
) – точка перегиба данной функции.
у


1 2 х
Асимптоты функций
Если кривая какой–либо своей частью неограниченно удаляется от начала координат, то эта часть может иногда иметь асимптоту – прямую, к которой кривая неограниченно приближается или с одной стороны, но не пересекая ее.
Различают вертикальные и наклонные асимптоты.
Определение 1 Прямая х = а называется вертикальной асимптотой графика функции f (х), если хотя бы один из пределов
 равен либо + ¥, либо – ¥.
равен либо + ¥, либо – ¥.
Пример Для функции 
 следовательно, прямая
следовательно, прямая 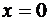 является ее вертикальной асимптотой.
является ее вертикальной асимптотой.
Определение 2 Прямая y = kх + b – называется наклонной асимптотой графика функции f (х) при х ® + ¥ (при х ® – ¥), если
f (х) = k х + b + a(х), где 
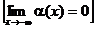 .
.
Теорема 1 Для того, чтобы прямая y = k х + b была наклонной асимптотой функции f (х) при х ® + ¥ (х ® – ¥), необходимо и достаточно, чтобы существовали два конечных предела 
Если в уравнении y = kх + b: k = 0, то наклонная асимптота вырождается в горизонтальнуюасимптоту
у = b.
Следствие Функция f (х) тогда и только тогда имеет горизонтальную асимптоту, когда  .
.
Пример Найти асимптоты функции 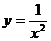 .
.
1)  ,
2) ,
2)  ,
3) ,
3)  , ,
 , ,
| следовательно, 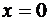 – вертикальная
асимптота.
следовательно, – вертикальная
асимптота.
следовательно,  – горизонтальная асимптота.
следовательно, наклонных асимптот нет. – горизонтальная асимптота.
следовательно, наклонных асимптот нет.
|  у
О х
О х
у
О х
О х
|
 2018-02-20
2018-02-20 347
347








