Исследование заданной функции и построение ее графика целесообразно проводить в следующем порядке:
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат. Выяснить, не является ли функция четной или нечетной, периодической.
3. Исследовать функцию на непрерывность найти точки разрыва, выяснить характер разрыва.
4. Найти асимптоты графика функции. Если их нет, то выяснить поведение функции в граничных точках области определения.
5. Найти критические точки первого рода. Определить интервалы монотонности функции и точки экстремума. Вычислить значения функции в этих точках.
6. Найти критические точки второго рода. Определить интервалы выпуклости вверх и вниз, точки перегиба функции. Вычислить значение функции в этих точках
7. Построить график функции. При необходимости, найти несколько вспомогательных точек графика.
Пример Провести полное исследование и построить график функции 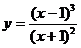 .
.
Исследование данной функции проведем в соответствии с предложенной схемой.
1. D (f) = (–¥;–1)È(–1;+¥).
2. y = 0 при х = 1, следовательно, (1;0) – точка пересечения графика с осью ОХ.
х = 0 при y = –1, следовательно, (0;–1) – точка пересечения графика с осью ОY.
Функция не является ни четной, ни нечетной, ни периодической.
3. Т.к. функция элементарная, то она непрерывна в области определения. х = –1 – точка разрыва функции.

следовательно  – точка разрыва второго рода.
– точка разрыва второго рода.
4. Из п.3 следует, что х = –1 – вертикальная асимптота.
Найдем наклонные асимптоты y = kх + b.
 Т.о., наклонной асимптотой при х ® + ¥ и при х ® – ¥ является прямая y = х – 5.
Т.о., наклонной асимптотой при х ® + ¥ и при х ® – ¥ является прямая y = х – 5.

Производная равна нулю при х = 1 и при х = –5, следовательно, х = 1 и х = –5 – стационарные точки. Производная 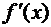 не существует при х = –1, т.е. х = –1 – критическая точка.
не существует при х = –1, т.е. х = –1 – критическая точка.
6)  –?
–?  .
.
Найдем  с помощью логарифмической производной, т.е. по формуле
с помощью логарифмической производной, т.е. по формуле
 .
.

Тогда  .
.  при х = 1.
при х = 1.
Результаты исследования оформим в виде таблицы
| х | (–¥;–5) | –5 | (–5;–1) | (–1;1) | 1 | (1;+¥) |

| + | 0 | – | + | 0 | + |
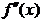
| – | – | – | – | 0 | + |
     
| 
| –13,5 | 0 |

 лок. max т. перегиба
лок. max т. перегиба
Точка (–5;–13,5) – точка локального максимума, (1,0) – точка перегиба.
Из таблицы видно, что точка (1;0) – точка перегиба ( при х <1,
при х <1, 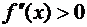 при х >1).
при х >1).
7) С учетом результатов исследования, построим график функции  .
.
у
х = –1
т.п.
–5 –1 1 5 х
лок. max –13.5
y = х – 5
 |
 2018-02-20
2018-02-20 420
420







