Теорема Гаусса в дифференциальной форме

Разделим обе части выражения (39.6) на объем V, находящийся внутри замкнутой поверхности S:

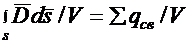
Устремим объем к нулю и найдем предел, к которому стремится это отношение:

.

 

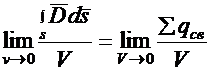При стремлении объема к нулю 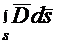 также стремится к нулю, но отношение двух бесконечно малых величин есть величина конечная.

Предел отношения потока вектора сквозь замкнутую поверхность, ограничивающую некоторый объем, к величине этого объема называют дивиргенцией вектора. Следовательно

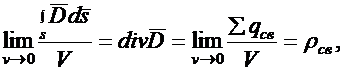
(39.11)

где 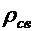 – объемная плотность свободных зарядов.

Выражение (39.11) означает, что истоки линий вектора 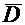 в данной точке поля определяются величиной объемной плотности свободных зарядов в этой точке.

Если в данной точке поля ρ > 0, то из бесконечно малого объема, окружающего данную точку линии вектора D исходят (рис. 39.2,а). Если ρ < 0, линии входят в объем (рис. 39.2,б) и, наконец, если

ρ =0, то через данную точку поля линии проходят (рис.39.2,в).

Если среда однородна и изотропна, то ε _а = const и

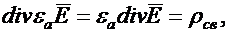 откуда

.

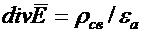(39.12)

В прямоугольной системе координат

.

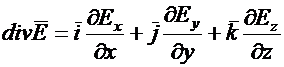В цилиндрической и сферической системах координат соответственно

.

 

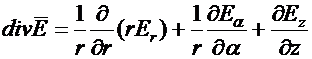
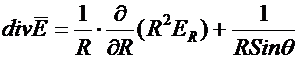Вопросы для самоконтроля

 

1. Какие электрические заряды называют свободными и почему?

2. Какие электрические заряды называют связанными?

3. В чем заключается явление поляризации?

4. В чем заключается явление электростатической индукции?

5. Каков физический смысл вектора поляризации ?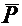

6. Что послужило основанием для введения вектора электрического смещения ?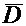

7. Сформулируйте теорему Гаусса в интегральной форме.

8. При каких условиях можно успешно использовать теорему Гаусса в интегральной форме? Приведите пример.

9. Прокомментируйте теорему Гаусса в дифференциальной форме. Каков ее физический смысл?

10. Дайте физическое толкование понятиям градиента и дивиргенции.