Логарифмическое дифференцирование; дифференцирование неявной функции; дифференцирование функции, заданной параметрически

Учебно-методическое пособие

По дисциплине ЕН.01 Математика

Специальности 23.02.03  «Техническое обслуживание и ремонт автомобильного транспорта»

Для группы Ма1-1уз

Содержание   стр.                

1.Тема 1.1. Основные понятия и методы математического анализа     3

2.Тема 1.2. Обыкновенные дифференциальные уравнения.                  31

3. Тема 1.3. Основные понятия дискретной математики.                       36

4. Тема 1.4. Основные понятия теории вероятностей и математической 50статистики

5. Тема 1.5 Основные численные методы.                                  63

 

Тема 1.1 Основные понятия и методы математического анализа.

1. Значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы. Производная функции. Основы дифференциального исчисления. Правила дифференцирования. Производная сложной функции.

Понятие производнойявляется одним из важнейших в кур­се математики. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.Производной функции y = f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю: . Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.Если  дифференцируемые функции своих аргумен­тов, то производная сложной функции существует и равна произ­ведению производной функции упо промежуточному аргументу и на произ­водную промежуточного аргумента и по независимой переменной х:

Аналогичная формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более.

Таблица формул дифференцирования

1. .                                                                                 

2. .                                                                                 

3.

4.

5.

6.

7.

8.

9. (

10.

11.

12.

13.

14.

15. (cos u)’=-sin u* u’.

16.

17.

18.

19.

20.

21.

 

Здесь u-дифференцируемая функция от x, ac — постоянная величина.

Пример 1. Найти производную функции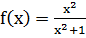

Решение. Дифференцируем функцию по формулам

Пример 2. Найти производную функции у = и вычислить ее значение при .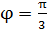

Решение. Это сложная функция с промежуточным аргументом . Дифференцируем ее по формулам .

Вычислим значение производной при .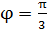

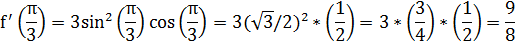
Пример 3. Найти производную функции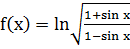

Решение. Сначала преобразуем функцию, используя свойства лога­рифмов:

Дифференцируя, получим

Логарифмическое дифференцирование; дифференцирование неявной функции; дифференцирование функции, заданной параметрически.