2018-02-20
378
1. 
2. 
.
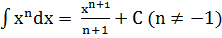3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
5. Методы интегрирования.
Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.
Пример 1. Найти 
Решение. Произведем подстановку 
Пример 2. Найти 
Решение. Сначала положим 
откуда 
Далее, получаем 
Пример 3. Найти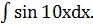 
.
Решение. Предположим 
Далее, получаем 
В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы (
постоянные):
1. 
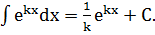
2. 
3. 
4. 
5. 
6. 
7. 
8. 
Так, при нахождении 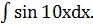Можно использовать формулу:
