Графы. Основные понятия. Способы задания графов

Графические представления в широком смысле - любые наглядные отображения исследуемой системы, процесса, явления на плоскости, К ним могут быть отнесены рисунки, чертежи, графики зависимостей характеристик, планы-кар­ты местностей, блок-схемы процессов, диаграммы и т.п. Такие изображения наглядно представляют различные вза­имосвязи, взаимообусловленности: топологическое (про­странственное) расположение объектов, хронологические (временные) зависимости процессов и явлений, логические, структурные, причинно-следственные (каузальные) и другие взаимосвязи.

Основные понятия графические представления - удобный способ иллюстрации содержания различных понятий, относящихся к другим способам формализованных представлений (см., например, диаграммы Венна и другие графические иллюстрации основ­ных теоретико-множественных и логических представлений).

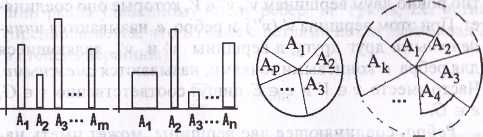
Все более распространенными становятся представления количественных характеристик, взаимосвязей между объек­тами в виде разного рода одно-, двух- и более мерных гисто­грамм (рис, 6.1), круговых диаграмм (рис. 6.2), других аналогичных

Рис. 6.1                                                      Рис. 6.2

способов представления в виде тех или иных гео­метрических фигур, по наглядным характеристикам которых (высоте, ширине, площади, радиусу и пр.) можно судить о ко­личественных соотношениях сравниваемых объектов, значи­тельно упрощая их анализ.Мощным и наиболее исследованным классом объектов, относящихся к графическим представлениям, являются так называемые графы, изучаемые в теории графов. Теория графов имеет огромные приложения, так как ее язык, с од­ной стороны, нагляден и понятен, а с другой - удобен в фор­мальном исследовании. На языке теории графов формули­руются и решаются многие задачи управления, в том числе задачи сетевого планирования и управления, анализа и про­ектирования организационных структур управления, ана­лиза процессов функционирования и целеполагания, мно­гие задачи принятия решений в условиях неопределеннос­ти и др.

Графические представления в узком смысле - это описа­ние исследуемой системы, процесса, явления средствами те­ории графов в виде совокупности двух классов объектов: вершин и соединяющих их линий - ребер или дуг. Графы и их составляющие характеризуются определенными свойства­ми и набором допустимых преобразований (операций) над ними.

Графом G называется совокупность двух множеств: вер­шин V и ребер Е, между элементами которых определено отношение инцидентности - каждое ребро е  Е инциден­тно ровно двум вершинам v', v" V которые оно соединя­ет. При этом вершина v' (v") и ребро е называются инци­дентными друг другу, а вершины v' и v", являющиеся для ребра е концевыми точками, называются смежными. Часто вместо v V  и е Е пишут соответственно v G, е G.

Ребро, соединяющее две вершины, может иметь на­правление от одной вершины к другой; в этом случае оно называется направленным, илиориентированным, или дугой и изображается стрелкой, направленной от вершины, называемой началом, к вершине, именуемой концом.

Граф, содержащий направленные ребра (дуги) с нача­лом v' и концом v", называется ориентированным (оргра­фом), а ненаправленные - неориентированным (назовем Н-графом).

Ребра, инцидентные одной и той же паре вершин, на­зываются параллельными, или кратными. Граф, содер­жащий кратные ребра, именуется мультиграфом. Реб­ро, концевые вершины которого совпадают, называется петлей.Граф называется конечным, если множество его элемен­тов (вершин и ребер) конечно, и пустым, если его множе­ство вершин V (а значит и ребер Е) пусто. Граф без петель и кратных ребер именуется полным, если каждая пара вершин соединена ребром.

Дополнением графа G называется граф , имеющий те же вершины, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получить пол­ный граф.

Каждому неориентированному графу канонически соответствует ориентированный граф с тем же мно­жеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инцидентными тем же вершинам и имеющими противоположные направ­ления.

ГрафыG₁ и G₂равны, равны, т.е. G₁ = G₂если их множе­ства вершин и ребер (выраженных через пары инциден­тных им вершин) совпадают: V₁ = V₂ и Е₁= Е₂ Графы G₁ и G₂ на рис. 6.3 равны. Граф G считается полностью заданным в строгом смысле, если нумерация его вер­шин и ребер зафиксирована. Графы, отличающиеся только нумерацией вершин и ребер, называются изомор­фными.

Пример 1. Задать граф G₁представ­ленный на рис. 6.3, через множества вершин V₁и ребер Е_1.

Граф G₁может быть полностью определен: двумя множествами -поимено­ванных вершин V₁ ={V₁,v₂, v₃, v₄,v₅ }и поименованных ребер E₁ = {е₁,e₂, e₃, e₄ }(в строгом смысле требуется установление от­ношения инцидентности ребер соответствующим вер­шинам);

 

• множеством ребер, каждое из которых представлено па­рой своих концевых вершин: Е= {(v_1, v₄), (v_4, v₃), (v₃, v₅), (v₅, v₂)}. 

Порядок указания вершин при описании ребра здесь без­различен, так как все ребра в графе G неориентированные.

Пример 2. На рис. 6. 4 изображены графы G₁ - G₁₂ с че­тырьмя вершинами в каждом. Сравнить графы.

Результаты сравнения графов таковы:

G₁ - G₇ - неориентированные; G₈- G₁₂ - ориентирован­ные;

G₁,G₂- полные, причем G₁ = G₂;G₇ - не является полным, так как хотя каждая пара вер­шин и соединена ребром, но имеется одна петля. (Иногда полным называют граф с петлями во всех вершинах, каждая пара которых соединена ребром. Граф G₇ не отвечает и это­му определению. В дальнейшем мы будем придерживаться определения полного графа, данного в начале параграфа.). G₃ - все вершины этого графа являются изолированными (граф с пустым множеством ребер, т.е. Е = 0); G₄ и G₅ являются дополнением друг другу: G₄= G_s и G₄= G₄;G₆ - мультиграф, так как содержит кратные ребра а и b, а также е и f;G₈ - ориентированный, канонически соответствующий неориентированному графу G₅;G₉иG_io не являются равными, так как имеют отличаю­щиеся ребра: (4,1) - в G₉ и (1,4) - в G_]0;G₁₁ - ориентированный мультиграф: ребра а и b -крат­ные, тогда как G12 мультиграфом не является, поскольку в нем ребра а и b различно ориентированы.

Пример 3. Чему равны степени вершин графов G₁, G₃ на рис. 6.5?

Рис. 6.5

Оба графа имеют по четыре вершины: V= {1,2,3,4}. Степени вершин неориентированного графа , р(2) = 4, р(3) Ц 3, р(4) = 4, если условиться считать вклад петли в степень вершины, равный 2, и р(4) = 3, если петля дает вклад 1 в степень вершины. Сумма степеней всех вер­шин графа  равна 14, т.е. вдвое больше числа ребер графа:

- число ребер графа.

Степени вершин ориентированного графа G₃:

Суммы степеней вершин первого и второго типа графа G₃ совпадают и равны числу от ребер графа:

Выше мы познакомились с двумя способами описания графов: графическим, и в виде двух множеств вершин V и ребер Е, когда каждое ребро е Е определено парой инци­дентных ему концевых вершин (v', v”). Рассмотрим другие способы, используемые в теории графов.

В общем виде задать граф - значит описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер достаточно их занумеровать.