2018-02-20
1029
Непосредственноевычисление определенного интеграла производится по формуле Ньютона—Лейбница:
где а - нижний предел, b 
верхний предел.
Из этой формулы виден порядок вычисления определенного интеграла: 1) находят одну из первообразных данной функции: 2) находят значения 
при 
3) вычисляют разность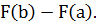 
Пример 1. Вычислить интеграл
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл
Приведем основные свойства определенного интеграла.
2. Отрезок интегрирования можно разбивать на части:
3. Постоянный множитель можно выносить за знак интеграла:
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:
Пример 2. Вычислить интеграл
Решение. 1) Произведем подстановку x3+2=t; тогда 
, 
2) Определим пределы интегрирования для переменной t. При x=1 получаем
3) Выразив подынтегральное выражение через tи dt и перейдя к новым пределам, получим:
Пример 3. Вычислить интеграл
Решение. 1) Положимcosx=t; тогда ─ sinxdx=dtиsinxdx= ─dt.
|
|
|
2) Определим пределы интегрирования для переменной t; tH=cos0=1; tB=cos(
)=0
3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим
Пример 4. Вычислить интеграл
Решение. Сначала преобразуем подынтегральное выражение:
Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:
Вычислим каждый интеграл отдельно:
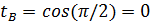
Тогда
Приложения определенного интеграла к решению задач.
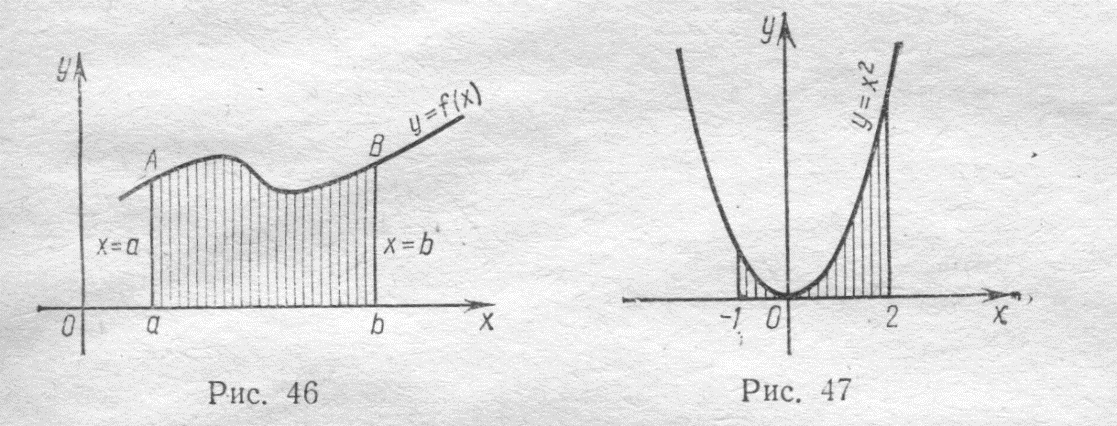
Площадь плоской фигуры. Площадь криволинейной трапеции аАВb (рис. 46), ограниченной графиком непрерывной функции ,y=f(x),где x 
отрезком [а,b] оси Ох, отрезками прямых х = а и х =b, вычисляется по формуле
Пример 5. Вычислить площадь фигуры, ограниченной параболой у = х3, прямыми х = — 1, х = 2 и осью абсцисс (рис. 47).
Решение. Применяя формулу (1), получаем
Площадь фигуры ABCD (рис. 48), ограниченной графиками непрерывных функций 
, отрезками прямых х = а и х = b, вычисляется по формуле
Пример 6. Вычислить площадь фигуры, ограниченной осью Ох и линией 
(рис. 49).
Решение. Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций 
. Для этого решим систему
Теперь найдем искомую площадь:
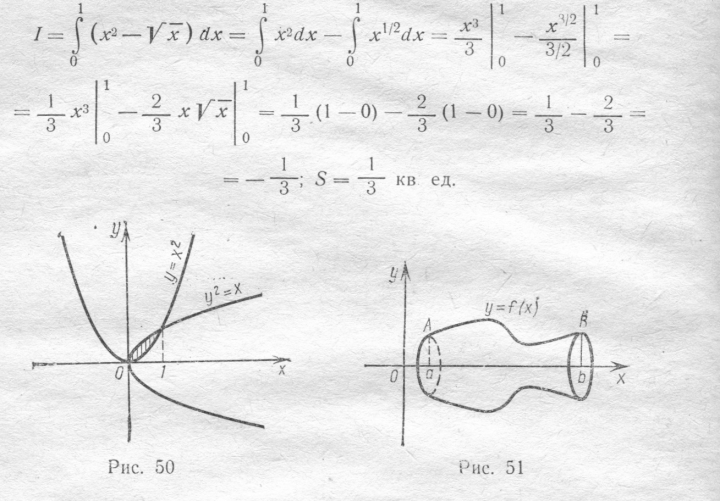
Пример 7. Вычислить площадь фигуры, ограниченной линиями у = х2 и у2 = х (рис. 50).
Решение. Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций у = х2 и у2 = х. Для этого решим систему
Искомую площадь вычисляем по формуле (2) при 
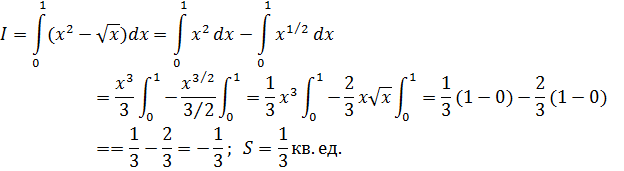
Путь, пройденный точкой. Если точка движется прямолинейно нее скоростьv=f(t) есть известная функция времени t, то путь, пройденный точкой за промежуток времени [t1,t2], вычисляется по формуле
|
|
|
Пример 10. Тело движется прямолинейно со скоростью v=0,1 t3м/с.
Вычислить путь, пройденный телом за первые 10 с.
Работа силы. Если переменная сила F= F(х) действует к направлении оси Ох, то работа силы на отрезке [а, b ]вычисляется по формуле
Пример 11. Какую работу нужно совершить, чтобы растянуть пружину на 0,06м, если сила 1 Hрастягивает её на 0,01 м?
Решение. Согласно закону Гука сила F, растягивающая или сжимающая пружину на х м, равна F=kx, где k–коэффициент пропорциональности.
Из условия следует 
и, следовательно, F=100 x,
Искомую работу находим по формуле (6);
Пример 12. Сила 196,2 Н растягивает пружину на 18 см. Какую работу она производит?
Решение. По закону Гука F=kx, откуда k = F/x = 196,2/0,18 = 1090. Значит, F= 1090х. Находим искомую работу
