Тема 1.2. Обыкновенные дифференциальные уравнения

1. Дифференциальные уравнения первого порядка с разделяющимися переменными.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую функцию, ее производную (или дифференциал аргумента и дифференциал функции).

Если дифференциальное уравнение содержит производную или дифференциал не выше первого порядка, то оно называется дифференциальным уравнением первого порядка. Общий вид такого уравнения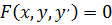

Общим решением дифференциального уравнения первого порядка называется функция y= (x,C) от xи произвольной постоянной С, обращающая это уравнение в тождество.Общее решение, записанное в неявном виде Ф(x,y,C)=0 называется общим интегралом

Частным решением уравнения F(x,y,y’)=0 называется решение, полученное из общего решения при фиксированном значении С: y= (x,C₀), где С₀ – фиксированное число.Частным интегралом уравнения F(x,y,y’)=0 называется интеграл, полученный из общего интеграла при фиксированном значении С: Ф(x,y,C₀)=0.График любого частного решения дифференциального уравнения F(x,y,y’)=0 называется интегральной кривой. Общему решению (и общему интегралу) этого уравнения соответствует семейство интегральных кривых, зависящих от одного параметра С.

Пример 1. Составить уравнение кривой y=f(x), если угловой коэффициент касательной, проведенной в любой точке кривой, равен 2x.

Решение. Так как на основании геометрического смысла производной y’=k_кас, то получим дифференциальное уравнение первого порядка:

Чтобы найти искомую функцию y=f(x), надо проинтегрировать обе части уравнения:

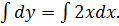Отсюда получим общее решение дифференциального уравнения: Геометрически это решение представляет собой семейство парабол (рис. 55) с вершиной на оси Oy, симметричных относительно этой оси.

Чтобы из общего решения выделить частное решение, надо задать начальные условия. Пусть y=-1; тогда общее решение примет вид , откуда Геометрически частное решение 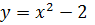представляет собой параболу, проходящую через точку (1;-1) (рис 55).

Дифференциальные уравнения с разделяющимися переменными. Общий вид такого уравнения где функции только от y.

Поделив обе части уравнения на произведение получим уравнение с разделенными переменными:

Общий интеграл этого уравнения имеет вид

Если произведение при x=aиy=b, то эти функции x=aиy=bявляются решениями дифференциального уравнения при условии, что при этих значениях x и y уравнение не теряет числового смысла. Геометрические эти решения представляют собой прямые, параллельные осям координат.

Пример 2. Решить уравнение 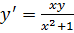Найти частное решение, удовлетворяющее условию y=3 при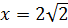

Решение. Так как , то откуда (x²+1)dy=xydx. Разделим обе части уравнения на произведение

Интегрируя, находим

После потенцирования получим решение откуда где .

Произведение так как при этом значении y дифференциальное уравнение не теряет числового смысла, то y=0 –решение уравнения. Но оно входит в решение при С=0. Значит, общее решение уравнения имеет вид .

Подставив в общее решение значения у=3 и х= 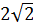, получим откуда . Частное решение уравнения, удовлетворяющее данному условию, имеет вид .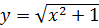

Пример 3. Решить уравнение . Найти частное решение, удовлетворяющее условию при ;

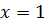Решение. Разделим каждый член уравнения на произведение

Интегрируя, находим

После потенцирования получим

Отсюда

Произведение так как при этом значении дифференциальное уравнение не теряет числового смысла, то решение уравнения. Но оно входит в интеграл

Подставив в общий интеграл значения 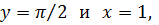получим откуда С=4. Частный интеграл уравнения, удовлетворяющий данному условию, имеет вид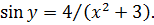

Пример 4. Решить уравнение . Найти частное решение, удовлетворяющее условию y=0 при х=0.

Решение. Перенесем второй член уравнения в правую часть и разделим обе части на произведение ):

Интегрируя, находим

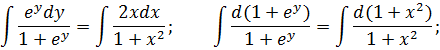
После потенцирования получим общий интеграл уравнения

Подставив в общий интеграл значения у = 0 и х =О, получим 1+1 = С, откуда С = 2. Частный интеграл уравнения, удовлетворяющий данному условию, имеет вид