Расчет на прочность и жесткость статически определимого бруса

 

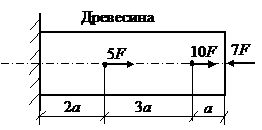
На брус круглого или квадратного поперечного сечения действуют осевые растягивающие и сжимающие силы F.

Требуется спроектировать брус равного сопротивления, для чего необходимо:

1. Определить продольные усилия N на каждом участке бруса и построить эпюру продольных сил.

2. Определить для каждого участка размеры поперечного сечения (диаметр для круглого и сторону квадрата для квадратного сечения) из расчета на прочность. Привести размеры поперечного сечения в соответствии с таблицей нормальных размеров.

3. Вычертить схему бруса по заданной длине и найденным размерам поперечного сечения в удобном масштабе.

4. Определить нормальные напряжения s на каждом участке бруса и построить их эпюру.

5. Определить абсолютные деформации участков бруса D l.

6. Определить перемещения сечений бруса d и построить их эпюру.

Данные для расчета приведены в таблице 2.1. Схемы нагружения бруса даны на рисунке 1.2.1.

Механические характеристики, допускаемые напряжения для материала бруса, таблица нормальных напряжений приведены в Приложении, табл.1.

 

Таблица 1.2.1

Числовые данные к расчету бруса равного сопротивления

Номер варианта	1	2		3	4	5		6	7	8		9	10
Нагрузка F, кН	35	50		40	45	32		60	28	25		55	30
Длина участка а, м	0,20	0,28		0,22	0,26	0,24		0,30	0,21	0,29		0,23	0,27
Форма поперечного сечения	круг	квадрат		круг	квадрат	квадрат		круг	круг	квадрат		круг	квадрат

 

 

Рис. 2.1. Схемы нагружения бруса к задаче 1.2.

 

 

Пример решения и методические указания к задаче 1.2

 

Исходные данные:

· схема нагружения бруса;

 

· ;

· ;

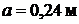· форма поперечного сечения – круг;

· механические характеристики и допускаемые напряжения для чугуна серого: .

 

Решение

1. Определение продольных сил на участках бруса.

Вычерчиваем расчетную схему бруса и разбиваем его на участки. Расчет производим от свободного конца бруса, т.е. справа. Используем метод сечений (рис. 1.2.2, а-г). Определяем значение продольных сил на участках. Продольную силу N будем направлять от сечения, т.е. первоначально считать, что участок растянут. Если при решении уравнения равновесия отсекаемой части продольная сила получается с отрицательным знаком, то, следовательно, участок сжатый.

Участок I (сечение I-I)

Участок II (сечение II-II)

Участок III (сечение III-III)

По полученным значениям строим эпюру продольных сил N (рис. 1.2.2, д).

2. Подбор сечения бруса равного сопротивления.

Участок I растянут. Условие прочности для этого участка имеет вид:

Отсюда

По таблице нормальных размеров принимаем ближайшее большее значение диаметра 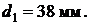 Перегрузка не должна превышать 5%.

Проверяем прочность

.

Недонапряжение составляет:

что допустимо.

Участок II сжат. Условие прочности для этого участка

Отсюда

По таблице нормальных размеров принимаем ближайшее большее значение диаметра

Проверяем прочность

Недонапряжение составляет:

Участок III растянут. Условие прочности для этого участка

Отсюда

По таблице нормальных размеров принимаем ближайшее меньшее значение диаметра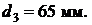

Проверяем прочность

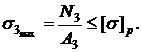
Перенапряжение составляет:

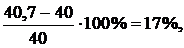
что допустимо.

По результатам расчета вычерчиваем схему бруса равного сопротивления (рис. 1.2.2, е).

3. Определяем значения нормальных напряжений на участках бруса

,

,

.

По полученным значениям строим эпюру нормальных напряжений s, рис. 1.2.2, ж.

4. Определяем абсолютные деформации участков бруса.

,

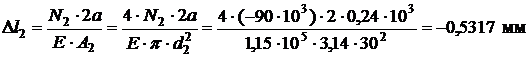5. Определяем перемещения сечений бруса d.

Расчет производим от жесткой заделки, т.е. слева, т.к. перемещение в эпюре равно нулю.

,

По полученным значениям строим эпюру перемещений d, рис. 1.2.2, з.

 

 

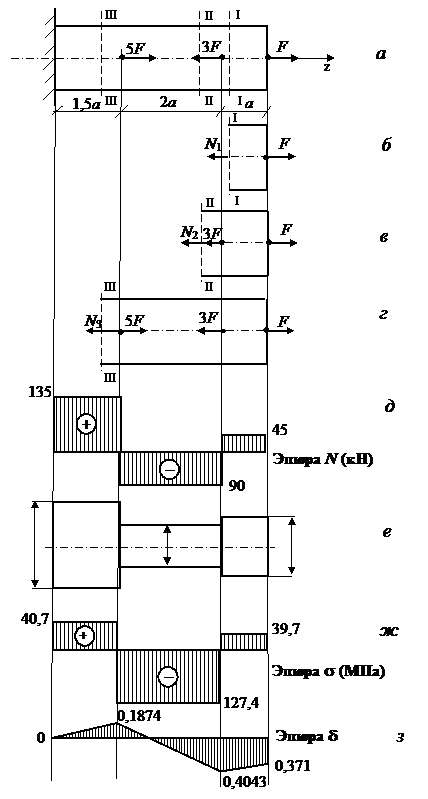Рис. 1.2.2. К примеру решения задачи 1.2.

Задача 1.3