Марковские случайные процессы

Под случайным (вероятностным или стохастическим) процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными закономерностями.

Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Это озна­чает, что состояние СМО меняется скачком в случайные моменты появления каких-то событий (например, прихода новой заявки, окончания обслуживания и т.п.).

Случайный процесс, протекающий в системе называется марковским случайным процессом (или «процессом без последействия»), если он обладает следующим свойством: для каждого момента времени: 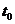 вероятность любого состояния системы в будущем (при 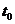>0) зависит только от ее состояния в настоящем (при t= 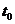) и не зависит от того, когда и каким образом система пришла в это состояние.

Пример марковского процесса: система S — счетчик в такси. Состояние системы в момент t характеризуется числом километ­ров (десятых долей километров), пройденных автомобилем до данного момента. Пусть в момент t₀ счетчик показывает S₀. Веро­ятность того, что в момент t > t₀   счетчик покажет то или иное число километров (точнее, соответствующее число рублей) S₁, зависит от S₀, но не зависит от того, в какие моменты времени изменялись показания счетчика до момента t₀.

Многие процессы можно приближенно считать марковскими. Например, процесс игры в шахматы; система S — группа шахмат­ных фигур. Состояние системы характеризуется числом фигур противника, сохранившихся на доске в момент t₀. Вероятность того, что в момент t> t₀ материальный перевес будет на стороне одного из противников, зависит в первую очередь от того, в каком состоянии находится система в данный момент t₀, а не от того, когда и в какой последовательности исчезли фигуры с доски до момента t₀.

Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы можно перечислить (перенумеровать), а система переходит из одного состояния в другое мгновенно (скачком).

Случайный процесс называется процессом, с дискретным временем, если переходы системы из состояния в состояние возможны только в строго определенные, фиксированные моменты времени. Эти моменты принято называть «шагами» или «этапами» процесса.

Случайный процесс называется процессом с непрерывным временем, если переход системы из состояния в состояние возможен в любой, наперед неизвестный, случайный момент времени.

Условимся обозначать как событие, состоящее в том, что после k шагов система находится в состоянии .

При любом k события  образуют полную группу и несовместны.

Процесс происходящий в системе, можно представить как последовательность (цепочку) событий. Если для каждого шага вероятность перехода из любого состояния  в любое состояние  не зависит от того, когда и как система пришла в состояние , то такая последовательность событий называется марковской цепью.

Вероятности переходов (переходные вероятности) можно запи­сать как условные вероятности

.

Легко видеть, что вероятности состояний системы после k-гo шага

если вероятности переходов от шага к шагу не меняются (цепь Маркова однородна).

Рассмотрим теперь непрерывную цепь Маркова.

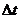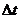Назовем плотностью вероятности перехода  предел отношения вероятности перехода системы за время  из со­стояния в состояние к длине промежутка . Тогда при ма­лом 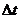вероятность перехода  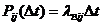с точностью до бесконечно малых высших порядков равна

Предположим, что нам известны плотности вероятностей пере­ходов для всех пар состояний системы, граф переходов которой показан на рис. 10.

Рис. 10

Поставим задачу: найти одну из вероятностей состояний, на­пример . Придадим t малое приращение 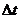и найдем вероят­ность того, что в момент t+  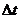система будет находиться в состоянии .

Могут представиться две возможности:

1) в момент t система уже была в состоянии , а за время 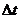не вышла из этого состояния; это происходит с вероятностью ;

2) в момент t система была в состоянии  , а за время 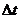 пере­шла из него в состояние . Вероятность совмещений этих событий  

Применяя правило сложения вероятностей, получим

)= +

Раскроем скобки в правой части, перенесем в левую и раз­делим обе части неравенства на 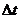; получим

Устремляя 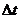к нулю и переходя к пределу, видим, что левая часть есть ни что иное как производная функции ,

,

т.е. получи дифференциальное уравнение первого порядка (уравнение, содержащее как саму неизвестную функцию, так и ее производную). Рассуждая аналогично, получим систему дифференциальных уравнений, на­зываемых уравнениями Колмогорова. Интегрирование этих урав­нений даст искомые вероятности состояний как функции времени. Начальные условия должны быть заданы: если в момент t = 0 сис­тема находилась в состоянии , то надо принять  .

Оказывается, что все уравнения построены по определенному правилу (правило составления дифференциальных уравнений Колмогорова): в левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько чле­нов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, соответствующий член имеет знак «минус»; если в состояние — знак «плюс». Каждый член равен произведению плотности вероятности перехода, соответствую­щей данной стрелке, умноженной на вероятность того состоя­ния, из которого исходит стрелка.

Это правило составления дифференциальных уравнений для ве­роятностей переходов является общим и справедливо для любой непрерывной марковской цепи.

Рассмотрим еще один пример марковского случайного процесса.

Построить граф состояний и составить систему дифференциальных уравнений Колмогорова следующего случайного процесса: устройство S состоит из двух узлов, каждый из которых в случай­ный момент времени может выйти из строя, после чего мгновен­но начинается ремонт узла, продолжающийся заранее неизвестное случайное время.

Решение. Возможные состояния системы: S₀ — оба узла исправны; S₁ — первый узел ремонтируется, второй исправен; S₂ — второй узел ремонтируется, первый исправен; S₃ — оба узла ремонтируются. Граф системы приведен на рисунке 5.2.

Рисунок 5.2. – Граф системы для примера 5.1.

Стрелка, направленная, например, из S₀ в S₁, означает переход системы в момент отказа первого узла, из S₁ в S₀ — переход в момент окончания ремонта этого узла.

На графе отсутствуют стрелки из S₀ в S₃ и из S₁ в S₂. Это объ­ясняется тем, что выходы узлов из строя предполагаются незави­симыми друг от друга и, например, вероятностью одновременного выхода из строя двух узлов (переход из S₀ в S₃) или одновремен­ного окончания ремонтов двух узлов (переход из S₃ в S₀) можно пренебречь.

Согласно правилу составления дифференциальных уравнений Колмогорова получим следующую систему:

В данной системе независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение .

Уравнения Колмогорова дают возможность найти все вероят­ности состояний как функции времени. Особый интерес представ­ляют вероятности системы p_i (t) в предельном стационарном режи­ме, т.е. при , которые называются предельными (или финаль­ными) вероятностями состояний.

В теории случайных процессов доказывается, что если число со­стояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные веро­ятности существуют.

Предельная вероятность состояния S_i имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состоя­ния S₀, т.е. р₀=0,5, то это означает, что в среднем половину вре­мени система находится в состоянии S₀.

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описы­вающих стационарный режим. Для системы S с графом состоя­ний, изображенном на рис. 5.2), такая система уравнений имеет вид:

Систему (15.10) можно составить непосредственно по раз­меченному графу состояний, если руководствоваться прави­лом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния p_it умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, вхо­дящих в i-e состояние, на вероятности тех состояний, из кото­рых эти потоки исходят.

Для математического описания марковского случайного про­цесса с дискретными состояниями и непрерывным временем, протекающего в СМО, познакомимся с одним из важных понятий теории вероятностей — понятием потока событий.

 

Потоки событий.

Под потоком событий понимается последовательность одно­родных событий, следующих одно за другим в какие-то случай­ные моменты времени (например, поток вызовов на телефонной станции, поток отказов ЭВМ, поток покупателей и т.п.).

Поток характеризуется интенсивностью l — частотой появле­ния событий или средним числом событий, поступающих в СМО в единицу времени.

Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени. Например, поток изделий на конвейере сборочного цеха (с посто­янной скоростью движения) является регулярным.

Поток событий называется стационарным, если его вероятно­стные характеристики не зависят от времени. В частности, интен­сивность стационарного потока есть величина постоянная: l(t)=l. Например, поток автомобилей на городском проспекте не являет­ся стационарным в течение суток, но этот поток можно считать стационарным в течение суток, скажем, в часы пик. Обращаем внимание на то, что в последнем случае фактическое число про­ходящих автомобилей в единицу времени (например, в каждую минуту) может заметно отличаться друг от друга, но среднее их число будет постоянно и не будет зависеть от времени.

Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени t₁ и t₂ — число событий, попадающих на один из них, не зависит от числа собы­тий, попадающих на другие (когда каждое последующее событие зависит только от непосредственно предшествующего, но не от более ранних). Например, поток пассажиров, вхо­дящих в метро, практически не имеет последействия. А, скажем, поток покупателей, отходящих с покупками от прилавка, уже имеет последействие (хотя бы потому, что интервал времени меж­ду отдельными покупателями не может быть меньше, чем мини­мальное время обслуживания каждого из них).

Поток событий называется ординарным, если вероятность по­падания на малый (элементарный) участок времени At двух и бо­лее событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Другими словами, поток событий ординарен, если события появляются в нем поодиночке, а не группами. Например, поток поездов, подходящих к станции, ор­динарен, а поток вагонов не ординарен.

Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия. Название "простейший" объясняется тем, что СМО с простейшими потоками имеет наиболее про­стое математическое описание. Заметим, что регулярный поток не является "простейшим", так как он обладает последействи­ем: моменты появления событий в таком потоке жестко зафик­сированы.

В теории массового обслуживания наибольшее число аналитических результатов получено для простейшего потока. Он обладает следующими свойствами: стационарностью, отсутствием после­действия (длина интервала времени до момента поступления сле­дующей заявки не зависит от того, поступила в начальный момент заявка или нет); ординарностью (в каждый момент времени в систему может поступить не более одной заявки). Для простейшего потока интервалы времени между двумя последовательными заяв­ками — независимые случайные величины с показательной функцией распределения 

.

                                                           

Математическое ожидание и дисперсия длины интервала времени между последовательными моментами поступления заявок

Простейший поток обладает устойчивостью: при суммировании независимых простейших потоков получается снова простейший поток с суммарной интенсивностью.

Для простейшего потока число заявок, поступающих в систему за промежуток времени , распределено по закону Пуассона:

,

где  — вероятность того, что за время  в систему поступит ровно k заявок. Математическое ожидание и дисперсия распределения Пуассона .

Распределение Пуассона дискретно. Заметим, что распределение Пуассона может описываться и нестационарный поток, у которого . Такой поток также является пуассоновским, но не является простейшим.

Если закон распределения промежутков времени между соседними заявками отличается от экспоненциального, то имеет место поток с ограниченным последействием (поток Пальма), или рекурсивный поток. Пример такого потока— поток Эрланга. Поток k-го порядка — это поток, у которого интервалы времени между моментами поступления двух последовательных заявок представляют собой сумму k независимых случайных величин, распределенных по показательному закону с параметром . Такой поток получить из простейшего потока выбрасыванием подряд (k-1) заявок с сохранением каждой k-й заявки.

Плотность распределения интервала времени между двумя соседними заявками в потоке Эрланга k -ro порядка

                                

При k =1 поток будет простейшим.