Одноканальная СМО с отказами

Проанализируем функционирование одноканальной СМО с отказами. Пусть СМО включает в себя только один канал (n = 1), и на ее вход подается пуассоновский поток заявок П_вх, интенсивность которого in П_вх = l. В общем случае интенсив­ность входящего потока может изменяться во времени, быть, таким образом, функцией времени /; чтобы это подчеркнуть, вместо lпишут l(t).

Заявка, поступившая на вход в момент, когда канал занят обслуживанием, получает отказ и покидает систему.

Пусть (непрерывная) случайная величина T_об — время об­служивания каналом одной заявки — распределена по показа­тельному закону:

, (t≥0)                                    (5.1)

с параметром l

Поток обслуживании (П_об), — поток обслуженных каналом заявок при условии, что канал не простаивает, т.е. занят об­служиванием непрерывно: по окончании обслуживания оче­редной заявки канал сразу же приступает к обслуживанию сле­дующей.

Таким образом, время обслуживания каналом одной заявки T_об является интервалом времени между двумя соседними со­бытиями в потоке обслуживании П_об.

Из формулы (5.1) следует, что поток обслу­живании П_об является простейшим с интенсивностью m: in П_об =m. Интенсивность m потока обслуживании П_об есть производительность канала. Имеет место равенство ; где  – среднее время обслуживания одной заявки, относя­щееся только к обслуженным заявкам, т.е. математическое ожидание М [ Тоб ] случайной величины Тоб.

Поток обслуживании П_об не следует путать с реальным вы­ходящим потоком П_вых обслуженных каналом заявок, посколь­ку в последнем интервал времени между двумя соседними об­служенными заявками может включать в себя кроме времени обслуживания и время простоя канала.

Состояния СМО будем характеризовать простаиванием или занятостью ее канала. Тогда СМО может находиться в одном из двух состояний: S₀ — канал свободен (простаивает); S₁ — канал занят.

Переход системы из состояния S₀ в состояние S₁ происходит под воздействием входящего потока заявок П_вх, а из состояния S₁ в состояние S₀ систему переводит поток обслуживании П_об: если в данный момент времени система находится в некотором состоянии, то с наступлением первого после данного момента времени события этого потока система туг же "перескакивает" в другое состояние. Плотности вероятностей перехода из состояния S₀ в состояние S₁ и обратно равны соответственно l и m. Поэтому размеченный граф состояний системы имеет вид, указанный на рисунке 5.2.

Размеченным графом состояний системы (в которой протекает случайный процесс с дискретными состояниями и непрерывным временем) называется схема, в которой состояния системы обозначаются квадратами (прямоугольниками, кругами), внутри которых помещается обозначение состояния, а стрелками указаны возможные непосредственные переходы из состояния в состояние, при этом у каждой стрелки указывается плотность вероятности перехода

Так как входящий поток заявок и поток обслуживании, пе­реводящие СМО из состояния в состояние, являются пуассоновскими, то в ней протекает марковский случайный процесс с дискретными состояниями и непрерывным временем), который, учитывая структуру графа состояний (рисунок 5.2.), является одновременно и циклическим процессом и процессом "гибели и размножения".

Случайный процесс, протекающий в системе с n состояниями s₁,..., s_n, называется циклическим, если граф состояний этой системы имеет вид:

Рисунок – Графическая интерпретация определения циклического процесса

Случайный процесс, протекающий в системе с n состояниями s₁,..., s_n, называ­ется процессом гибели и размножения, если граф состояний этой системы имеет вид:

Рисунок - Графическая интерпретация определения процесса гибели и размножения

Под размножением можно понимать процесс увеличения числа занятых каналов, т.е. переходы СМО из состояния в состояния по стрелкам слева направо, а гибель интерпретировать, как уменьшение числа занятых каналов, т.е. переходы системы по стрелкам справа налево.

Рисунок 5.2.— Схема процесса гибели и размножения для Одноканальной СМО.

Обозначим через р₀(t) и p₁(t) — вероятности событий, со­стоящих в том, что в момент времени t СМО находится соот­ветственно в состояниях s₀и s₁ .Эти вероятности называются вероятностями состояний (см. [5], с. 42). Очевидно, что вероят­ности состояний для любого момента времени t удовлетворяют нормировочному условию:

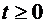,                                     (5.2)

Вероятности состояний p₀(t) и p₁⁽t) являются основными ха­рактеристиками случайного процесса, протекающего в СМО. Так как этот процесс марковский, то вероятностные функции времени р₀(t) и p₁(t) можно найти изсистемы дифференциальных   уравнений Колмогорова:

                                                              (5.3)

составляемой по одному из правил, данных в [5], с. 45, 46. В силу нормировочного условия (5.2) уравнения системы (5.3) зависимые, и потому одно из них, например второе, можно отбросить.

Из условия (5.2):

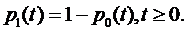                                              (5.4)

Подставив выражение (5.4) в первое уравнение системы (5.3), получим дифференциальное уравнение

,                       (5.5)

с неизвестной функцией р₀(t). Это уравнение будем решать при естественномпредположении, что в начальный момент времени t=0 канал был свободен и, следовательно, начальные условия будут выглядеть так:

  p ₁(0) = 0                                  (5.6)

Для упрощения решения уравнения (5.5) предположим также, что входящий поток заявок П_вх - простейший, т.е. что пуассоновский поток П_вх является к тому же стационарным. Это означает, что интенсивность λпотока П_вх не изменяется с течением времени, т.е. является постоянной: . В этом случае , где  - среднее время простаивания (свободного состояния) канала или, что то же самое, средний интервал времени между любыми двумя соседними заявками, поступающими на вход СМО (т.е. математическое ожидание М [Т _пр ] непрерывной случайной величины Т _пр пред ставляющей собой интервал времени между любыми двумя соседними заявками во входящем потоке П_вх).

Уравнение (5.5) представляет собой линейное дифференци­альное уравнение первого порядка с постоянными коэффици­ентами. Из теории дифференциальных уравнений (например, см. [14], с. 56) известно, что общее решение такого уравнения имеет вид:

.

Отсюда

                (5.7)

Подставим в равенство (5.7) первое из начальных условий (5.6) p₀(0)=1, получим:

откуда .

С учетом найденного значения постоянной С равенство (5.7) принимает вид:

.

Тогда из равенства (5.4):

.

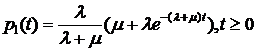Итак, частным решением системы (5.3), удовлетворяющим начальным условиям (5.6), является

                                            (5.8)

Так как 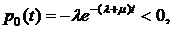, то функция р₀(t) убывает.

А так как > 0, t > 0, то функция р₀(t) выпукла вниз.

Аналогично из того, что > 0, t>0, мы делаем вывод о возрастании функции р₁(t),   а из того, что < 0, следует, что функция р₁(t) выпукла вверх.

При t = 0   из системы (5.8) находим: р ₀(0)= 1; р₁ (0) = 0,

что соответствует начальным условиям (5.6). Так как из первого уравнения системы (5.8):

то прямая  является горизонтальной асимптотой графикафункции р _о (t). Аналогично из второго уравнения системы (5.8)

и потому прямая  является горизонтальной асимптотой графика функции р ₁ (t). Рассмотрим т р и случая:

случай 1: λ > µ

случай 2: λ = µ

случай 3: λ < µ

Построим в одной системе координат графики функций р _о (t) и р ₁ (t).

Случай 1. Так как λ > µ > 0, то  >   > 0, прямая  лежит выше прямой  и они лежат в верхней полуплоскости. Поэтому графики функций p₀(t) и p₁(t) пересекаются и пересекают соответственно прямые и . Асимптота  отстоит от прямой y = 1 на расстоянии 1 - = , т.е. на та­ком же расстоянии, что и асимптота  от горизонтальной оси координат. Абсциссу t₁ точки А пересечения графика функции p₀(t) с прямой  находим из уравнения :

,

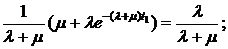
прологарифмировав это равенство, получим

откуда

Отметим, что в силу неравенства λ > µ отношение > 1 и потому существует и больше 0, а следовательно, t₁ > 0.

Аналогичным образом из уравнения  нахо­дим абсциссу точки В пересечения графика функции p₁(t) с прямой  и убеждаемся, что она равна абсциссе t₁ (рис. 3.2). Таким образом, точки А и В лежат на одной вертикали.

Теперь найдем абсциссу t₂ точки С пересечения графиков функций p₀(t) и p₁(t). Так как p₀(t₂) = p₁(t₂), то из нормировоч­ного условия (5.2) заключаем, что p₀(t₂) = p₁(t₂) = 1/2. Тогда t₂ можно найти, например, из уравнения p₁(t₂) = 1/2:

откуда

.

 

Сети СМО

При исследовании различных объектов управления часто встречаются с прохождением заявок последовательно через несколько систем обслуживания. Например, технологический процесс обработки деталей содержит 2 стадии, на каждой из которых производится обработка деталей на соответствующей груп­пе оборудования (рис. 1.2). После второй СМО производится технический кон­троль, и заявки либо проходят на дальнейшую обработку (с вероятностью θ),

либо возвращаются на повторное выполнение операций (отбраковываются с вероятностью

1- θ).

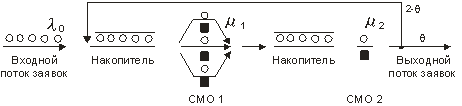
Рис. 1.2. Пример сети СМО

 

В этом случае СМО образуют сеть, которая характеризуется связями ме­жду отдельными СМО и свойствами самих систем. Сеть СМО удобно пред­ставлять в виде графа передач (рис. 1.3), где вершины графа соответствуют СМО, дуги указывают возможности перехода заявки из одной СМО в другую, а числа в дугах - вероятности перехода.

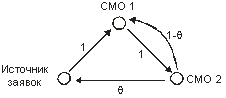
Рис. 1.3. Граф передач

 

Рассмотрим сеть систем массового обслуживания, которая включает М СМО и один источник заявок. Заявки, выходящие из i -й системы (i =1,2,.. М) с постоянной вероятностью θ_ij, поступают в систему j или покидают сеть (j=0). Из источника в j -ю систему заявки поступают с вероятностью θ_oj. Матрицу ве­роятностей поступления требований из одной системы в другую называют мат­рицей передач:

Т=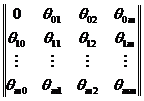

где θ₀₀=0 - Циркулирование потока заявок в источнике,

 

Для графа передач, представленного на рис. 1.3, матрица передач будет следующей:

Т=

Для определения характеристик сети СМО необходимо определить интенсивности потоков заявок в каждой системе, т.е. среднее число заявок поступающих в систему за единицу времени в установившемся режиме λ_{i .} Среднее число заявок, покидающих систему, равно среднему числу поступаю­щих заявок, и, следовательно,

В матричной форме это выражение:

λ=λТ.

Интенсивности потоков заявок в СМО зависят от λ₀ следовательно можно определить:

λ_i = a_i λ_0, i = l, 2,..., т,

где λ₀- интенсивность источника заявок (интенсивность потока, поступающе­го на вход сети).

Допустим, сеть замкнута, и в ней циркулирует конечное число заявок.

Тогда

Т=

Здесь интенсивности потоков определяются общим числом требований в сети. Выбрав некоторую СМО i₀  за базовую, можно определить

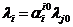
Важной характеристикой сети СМО служит среднее время пребывания в ней заявки. Пусть сеть разомкнута. В установившемся режиме вероятность на­хождения заявки в СМО определяется

Р = РТ

Сравнивая с λ = λ Т, получаем:

где p_i: - вероятность нахождения заявки в j -и СМО.

 

Относительная частота прохождения требования через систему j за доста­точно большой интервал времени t

где n_j –число случаев, когда заявка оказалась в системе j;

N - общее число заявок, прошедших через сеть.

  Тогда:

 

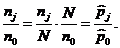
При достаточно большом интервале времени:

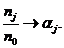
Таким образом, требования, поступающие из источника, a_j раз проходят

через систему с номером j, прежде чем вернуться в источник. Следовательно,

где 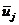 - среднее время пребывания заявки в СМО с номером j.

Сложность расчета сетей СМО заключается в том, что простейший поток заявок, поступающий в систему, на ее выходе в общем случае будет обладать последействием. А в этом случае нельзя применять рассмотренный выше аппа­рат анализа марковских СМО. Однако, если на всех приборах сети длитель­ность обслуживания распределена по показательному закону, то выходящие из СМО потоки заявок будут пуассоновскими. Такие сети называются показатель­ными.

Для показательных сетей существует установившийся режим, если для

каждой i -й СМО загрузка  и этот режим представляет собой суперпозицию установившихся режимов (одновременность) составляющих систем, рассматриваемых как взаимно независимые и нагруженные источниками с пуассоновскими потоками с интенсивностями λ_i, таким образом, определив λ_i, для каждой системы, можно рассчитывать характеристики каждой отдельной СМО по полученным ранее формулам (подразделы 1.5.1 - 1.5.10).

Состояния сети можно задать вектором, каждая составляю­щая которого представляет собой число требований в соответствующей СМО:

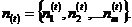
Вероятность этих состояний сети в установившемся режиме обозначим

Для разомкнутых показательных сетей

 

где   - вероятность n_i -го состояния i-й СМО, рассчитанная при условии, что эта система нагружена пуассоновским источником с интенсивностью λ_i.