2020-01-15
548
а) для повторного собственно случайного отбора:
,
б) для бесповторного собственно случайного отбора:
,
где 
– дисперсия генеральной совокупности,
– число единиц выборочной совокупности,
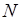– число единиц генеральной совокупности,
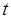– коэффициент доверия, величина которого зависит от заданной доверительной вероятности 
.
Приведем значения некоторых коэффициентов доверия (см. табл. 2.1)
Таблица 2.1
Доверительная вероятность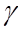 
| Коэффициент доверия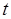 
|
| 0,683 | 1,0 |
| 0,866 | 1,5 |
| 0,954 | 2,0 |
| 0,991 | 2,6 |
| 0,997 | 3,0 |
Замечание. Если генеральная дисперсия неизвестна, то вместо нее можно взять исправленную выборочную дисперсию. При больших выборках
( >30) отношение 
, и вместо генеральной дисперсии можно использовать выборочную дисперсию.
Пример 2.1
Из общей численности рабочих предприятия 5000 человек в порядке собственно случайного бесповторного отбора было отобрано 500 человек для изучения времени простоев в течение рабочего дня. Результаты наблюдения отражены в табл. 2.2
Таблица 2.2
Распределение выборочной численности рабочих
предприятия по времени простоев
| Группы рабочих по времени простоев в минутах | Число рабочих ( )
| Среднее значение интервала в минутах ( )
|
| до 10 от 10 до 20 от 20 до 30 от 30 до 40 от 40 до 50 от 50 до 60 свыше 60 | 35 62 84 145 77 65 32 | 5 15 25 35 45 55 65 |
| Итого: | 500 |
С вероятностью 0,997 определить пределы, в которых находится среднее время простоя одного рабочего на предприятии.
Решение
1) Выборочная средняя времени простоя одного рабочего:
(мин).
2) Выборочная дисперсия времени простоя одного рабочего:
.
3) Предельная ошибка выборочной средней с вероятностью 
=0,997 для бесповторного отбора:
;
где коэффициент доверия 
=3 найден по табл. 2.1 в соответствии с доверительной вероятностью 
=0,997.
4) Среднее время простоя одного рабочего на предприятии с вероятностью 0,997 находится в интервале от 32,77 минут до 36,84 минут, что вытекает из интервальной оценки генеральной средней:
,
т.е. 34,8–2,03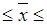 
34,8+2,03.
Аналогично находится интервальная оценка генеральной доли:
,
где 
выборочная доля, которая находится по формуле:
– число единиц выборочной совокупности,
– число единиц, обладающих указанным признаком,
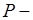генеральная доля,
– предельная ошибка выборочной доли для заданной доверительно вероятности .
