 .
.
Ответ:  .
.
Алгебраическое решение
Данное уравнение легко «превратить» в рациональное уравнение восьмой степени возведением обеих частей исходного уравнения в квадрат. Поиск корней получившегося рационального уравнения затруднен, и необходимо обладать высокой степенью изобретательности, чтобы справиться с задачей. Поэтому целесообразно знать иной способ решения, менее традиционный. Например, подстановку 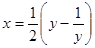 , предложенную И. Ф. Шарыгиным [57].
, предложенную И. Ф. Шарыгиным [57].
Положим  , тогда
, тогда
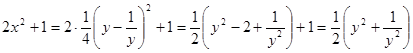
 Преобразуем правую часть уравнения
Преобразуем правую часть уравнения 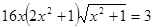 :
:
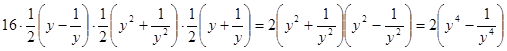 .
.
С учетом преобразований уравнение  примет вид
примет вид
 .
.
Введем замену  , тогда
, тогда
 .
.
Второй корень является лишним, поэтому  , а
, а  .
.
Ответ:  .
.
Если заранее не известна идея решения уравнения 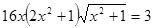 , то решать стандартно возведением обеих частей уравнения в квадрат проблематично, так как в результате получается уравнение восьмой степени
, то решать стандартно возведением обеих частей уравнения в квадрат проблематично, так как в результате получается уравнение восьмой степени 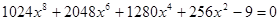 , найти корни которого чрезвычайно сложно. Решение с помощью тригонометрической подстановки выглядит громоздким. Могут возникнуть трудности с поиском корней уравнения
, найти корни которого чрезвычайно сложно. Решение с помощью тригонометрической подстановки выглядит громоздким. Могут возникнуть трудности с поиском корней уравнения  , если не заметить, что оно является возвратным. Решение указанного уравнения происходит с применением аппарата алгебры, поэтому можно сказать, что предложенное решение является комбинированным. В нем сведения из алгебры и тригонометрии работают совместно на одну цель – получить решение. Также решение указанного уравнения требует аккуратного рассмотрения двух случаев. Решение заменой
, если не заметить, что оно является возвратным. Решение указанного уравнения происходит с применением аппарата алгебры, поэтому можно сказать, что предложенное решение является комбинированным. В нем сведения из алгебры и тригонометрии работают совместно на одну цель – получить решение. Также решение указанного уравнения требует аккуратного рассмотрения двух случаев. Решение заменой  технически проще и красивее, чем с помощью тригонометрической подстановки. Желательно, чтобы учащиеся знали такой способ замены и применяли его для решения задач.
технически проще и красивее, чем с помощью тригонометрической подстановки. Желательно, чтобы учащиеся знали такой способ замены и применяли его для решения задач.
Подчеркнем, что применение тригонометрической подстановки для решения задач должно быть осознанным и оправданным. Использовать подстановку целесообразно в тех случаях, когда решение другим способом сложнее или вовсе невозможно. Приведем еще один пример, который, в отличие от предыдущего, проще и быстрее решается стандартным способом.
Пример 5. Решить уравнение
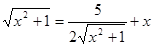 [51].
[51].
Решение с помощью тригонометрической подстановки
Так как переменная  может принимать любые действительные значения, можно положить
может принимать любые действительные значения, можно положить  . Уравнение примет вид
. Уравнение примет вид
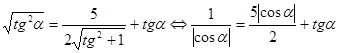 .
.
В силу того, что  , можно раскрыть модуль
, можно раскрыть модуль
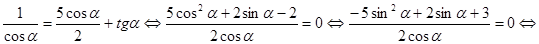
 .
.
Так как 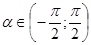 , то
, то  .
.
Ответ:  .
.
 2020-01-15
2020-01-15 111
111








