Так как выражение от правой части равенства четное и  и
и  , выясним вопрос о наличии корней на промежутке
, выясним вопрос о наличии корней на промежутке  . Проверкой устанавливаем, что
. Проверкой устанавливаем, что  – корень. Рассмотрим функции от правой и левой частей уравнения, то есть функции
– корень. Рассмотрим функции от правой и левой частей уравнения, то есть функции 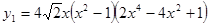 и
и  . Так как
. Так как

и функция  непрерывна на числовой прямой, то найдутся такие значения
непрерывна на числовой прямой, то найдутся такие значения  и
и  , что
, что 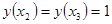 . Поэтому на промежутке
. Поэтому на промежутке  уравнение имеет три корня, а на всей числовой прямой – шесть корней.
уравнение имеет три корня, а на всей числовой прямой – шесть корней.
Ответ: 6 корней.
В данном случае можно решать любым способом, но если количество корней на небольшом промежутке достаточно велико, вычисления могут оказаться громоздкими, и сам метод неэффективным. В этом случае на помощь приходит метод тригонометрической подстановки. Надо заметить, что решить вопрос о количестве корней можно с помощью производной, но в данном случае такое решение мало эффективно, так как затруднительно найти нули производной.
Пример 2. Решить уравнение
 .
.
Если для выше приведенных задач не удается найти нетрадиционный путь решения, то все равно остается вероятность справиться с задачей с помощью стандартных школьных рассуждений, правда, затратив при этом гораздо больше времени. Эта задача лишает такого выбора, так как ее решение другим способом не представляется возможным.
Решение с помощью тригонометрической подстановки
Поделим все члены уравнения на 2. Уравнение примет вид
 .
.
Докажем, что все корни данного уравнения по модулю не превосходят единицы. Пусть  , тогда
, тогда  . Получили, что при
. Получили, что при  левая часть уравнения по модулю больше единицы, а правая – меньше единицы, что невозможно.
левая часть уравнения по модулю больше единицы, а правая – меньше единицы, что невозможно.
Положим  . Уравнение примет вид
. Уравнение примет вид
 .
.
Условию  удовлетворяют три значения
удовлетворяют три значения
 .
.
Поскольку кубическое уравнение не может иметь больше трех различных корней, то мы нашли все решения.
Ответ:  .
.
1.3 Показательные уравнения
Приведем пример задания, решить которое без введения тригонометрической подстановки не представляется возможным.
Пример 1. Решить уравнение 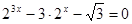 .
.
Пусть  , тогда уравнение перепишется в виде
, тогда уравнение перепишется в виде
 .
.
Введем замену  , получим
, получим
 .
.
Это уравнение мы уже решали[1]. Его корни
 .
.
Два последних значения меньше нуля, поэтому нам подходит только  . Перейдем к переменной
. Перейдем к переменной  , а затем к переменной
, а затем к переменной 
 .
.
Ответ:  .
.
Решение систем
В данном параграфе предложены системы повышенной сложности, решить которые, не зная специальных методов решения, сложно.
Пример 1. Решить систему уравнений
 [3].
[3].
Решение с помощью тригонометрической подстановки
Так как квадрат суммы чисел  и
и  равен единице, то каждое из этих чисел по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Поэтому можно положить
равен единице, то каждое из этих чисел по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Поэтому можно положить  Второе уравнение системы примет вид
Второе уравнение системы примет вид
 .
.
Условию  удовлетворяют четыре значения
удовлетворяют четыре значения
 .
.

 .
.

 .
.

 .
.

 .
.
Ответ: 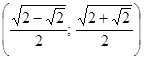 ;
; 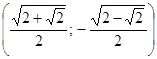 ;
; 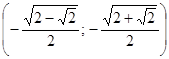 ;
; 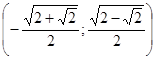 .
.
 2020-01-15
2020-01-15 186
186








