2020-01-15
193
.
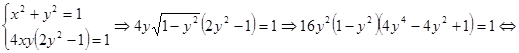
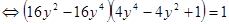Пусть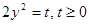 
, тогда 
. Имеем
.
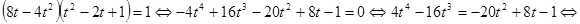
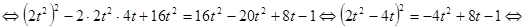
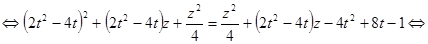
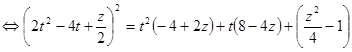Подберем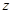 
так, чтобы многочлен, стоящий в правой части равенства, стал полным квадратом. Для этого он должен иметь один двукратный корень, то есть
.
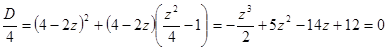Подбором находим, что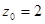 
является корнем уравнения
.
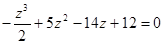Подставим 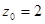в уравнение 
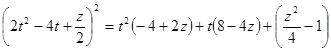, после чего оно примет вид
.
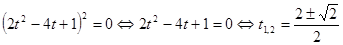Перейдем к переменной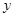 
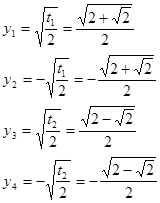
Подставив получившиеся значения переменной 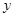во второе уравнение системы, найдем соответствующие значения переменной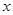 
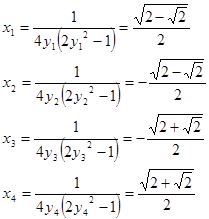
Ответ: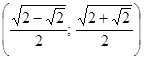 
; 
; 
; 
.
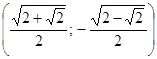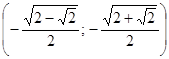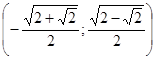Пример 2. Сколько решений имеет система уравнений
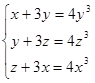[18].
Здесь представлена так называемая циклическая система уравнений. Подобные системы часто предлагаются на вступительных экзаменах в вузы с повышенными требованиями по математике [30]. Решить эти системы, не зная специальных методов решения, очень сложно. В данном случае подбором устанавливается решение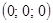 
. Попытки доказать, что система не имеет других решений, положительных результатов не дают. Неоценимую помощь в решении такого класса задач оказывает метод тригонометрической подстановки.
Перепишем систему в виде
.
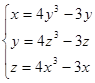Докажем, что все числа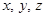 
по абсолютной величине не превосходят единицы. Пусть 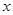– максимальное из чисел 
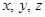и 
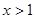, то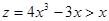 
. Пришли к противоречию. Если число 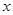– минимальное и 
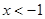, то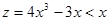 
. Опять пришли к противоречию. Итак 
.
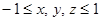Решение с помощью тригонометрической подстановки
Положим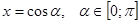 
. Тогда 
, 
, 
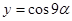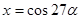. Число решений исходной системы равно числу решений уравнения
.
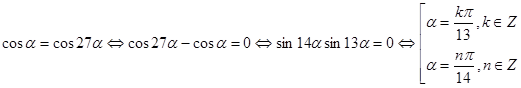Условию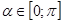 
удовлетворяет 27 решений
.
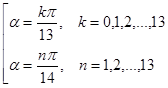Ответ: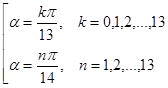 
.
Алгебраическое решение
Выразим переменную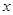 
.
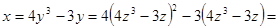
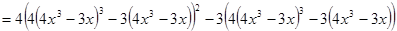Выяснить количество корней полученного уравнения с помощью производной или другим способом чрезвычайно трудно, поэтому в данном случае самый эффективный способ решение – решение с помощью тригонометрической подстановки.
