Вероятностное моделирование ошибок

Мы уже неоднократно сталкивались с вопросом о том, сколь существенно величина коэффициента корреляции (детерминации) должна отличаться от нуля, чтобы можно было говорить о действительно существующей линейной связи между исследуемыми переменными.

Если оцененное значение эластичности потребления некоторого товара оказалось несколько больше единицы, то возникает вопрос о том, сколь надежным является заключение о том, что потребление этого товара эластично по ценам.

Если мы будем использовать подобранную прямую

для прогнозирования значений  для новых наблюдений , t= n +1,..., n + k, то сколь надежными будут такие прогнозы?

Если у нас нет теоретических (экономических) оснований для выбора между моделью в уровнях переменных и моделью в логарифмах уровней, то как выбрать одну из этих моделей на основании одних только наблюдений?

Ответы на эти и другие подобные вопросы невозможны, если мы не сделаем некоторых более или менее подробных предположений о структуре последовательности ошибок , участвующих в определении модели наблюдений

Базовая, и наиболее простая модель для последовательности  предполагает, что  — независимые случайные величины, имеющие одинаковое распределение (i. i. d. — independent, identically distributed random variables).

Для нас (пока!) достаточно представлять случайную величину   как переменную величину, такую, что до наблюдения ее значения невозможно предсказать это значение абсолютно точно, и, в то же время, для любого , , определена вероятность

того, что наблюдаемое значение переменной   не превзойдет ; . Функция  , называется функцией распределения случайной величины   (c. d. f. — cumulative distribution function).

Говоря об ошибках   как о случайных величинах, мы, соответственно, понимаем указанную линейную модель наблюдений таким образом, что

а) существует (теоретическая, объективная или в виде тенденции) линейная зависимость значений переменной  от значений переменной   с вполне определенными, хотя обычно и не известными исследователю, значениями параметров   и ;

б) эта линейная связь для реальных статистических данных не является строгой: наблюдаемые значения  переменной   отклоняются от значений , указываемых моделью линейной связи

в) при заданных (известных) значениях   конкретные значения отклонений

не могут быть точно предсказаны до наблюдения значений  даже если значения параметров   и   известны точно;

г) для каждого , определена вероятность   того, что наблюдаемое значение отклонения   не превзойдет , причем эта вероятность не зависит от номера наблюдения;

д) вероятность того, что наблюдаемое значение отклонения  в i- м наблюдениине превзойдет , не зависит от того, какие именно значения принимают отклонения в остальных   наблюдениях.

В дальнейшем, говоря о той или иной случайной величине , мы будем предполагать существование функции , принимающей только неотрицательные значения и такой, что

1) площадь под кривой

в прямоугольной системе координат  (точнее, площадь, ограниченная сверху этой кривой и снизу — горизонтальной осью ) равна ,

2) для любой пары значений   с , вероятность

численно равна площади, ограниченной снизу осью , сверху — кривой , слева — вертикальной прямой , справа — вертикальной прямой  (т. е. равна части площади под кривой , расположенной между точками   и ).

3) для любого , вероятность  того, что наблюдаемое значение   не превзойдет , равна площади, ограниченной снизу осью , сверху — кривой  и справа — вертикальной прямой , т. е. равна части площади под кривой , расположенной левее точки .

Заметим, что при этом выполняется следующее важное соотношение:

(Действительно, вероятность  численно равна части площади под кривой , расположенной левее точки , а эта часть складывается из части площади под кривой, расположенной левее точки  и части площади под кривой, расположенной между точками   и , так что

откуда и следует заявленное соотношение.) Кроме того,

(Действительно,

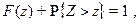
поскольку слева складываются части площади под кривой , расположенные, соответственно, левее и правее точки , так что в сумме они составляют всю площадь под этой кривой, а вся площадь под кривой  как раз и равна 1.)

Функция  связана с функцией распределения случайной величины   соотношениями

и называется функцией плотности вероятности случайной величины   (p.d.f. — probability density function). Для краткости, мы часто будем говорить о функции  как о функции плотности или о плотности распределения случайной величины .

Возьмем два непересекающихся интервала значений переменной :  и . Рассмотрим два варианта распределения вероятности случайной величины : равномерное распределение на отрезке  и треугольное распределение на том же отрезке. Графики функций плотности для этих двух вариантов имеют следующий вид:

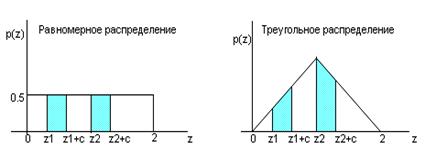
Площади заштрихованных прямоугольников на первом графике численно равны вероятностям того, что случайная величина , имеющая равномерное распределение на отрезке , примет значения в пределах  и , соответственно. Поскольку основания и высоты этих прямоугольников равны, то равны и их площади, т.е. равны указанные вероятности.

Площади заштрихованных трапеций на втором графике численно равны вероятностям того, что случайная величина , имеющая треугольное распределение на отрезке , примет значения в пределах  и 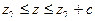, соответственно. Высоты этих трапеций равны, однако стороны трапеции, расположенной правее, больше сторон трапеции, расположенной левее. Поэтому и площадь трапеции, расположенной правее, больше площади трапеции, расположенной левее. А это означает, в свою очередь, что вероятность того, что случайная величина , имеющая треугольное распределение на отрезке , примет значения в пределах 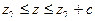, больше вероятности того, что эта случайная величина   примет значения в пределах .

Таким образом, функция плотности указывает на более вероятные и менее вероятные интервалы значений случайной величины. Если случайная величина   имеет равномерное распределение на отрезке , то для нее все интервалы значений, имеющие одинаковую длину и расположенные целиком в пределах отрезка , имеют одинаковые вероятности (т. е. вероятности попадания значений случайной величины на эти интервалы одинаковы). Если же случайная величина   имеет треугольное распределение на отрезке , то для нее интервалы значений, имеющие одинаковую длину и расположенные целиком в пределах отрезка , имеют, вообще говоря, различные вероятности: вероятность того, что случайная величина примет значение в интервале, расположенном ближе к центральному значению , больше вероятности того, что случайная величина примет значение в интервале, расположенном ближе к одному из концов отрезка .

Обсудим несколько более точно вопрос о том, что мы понимаем под независимостью нескольких случайных величин. Пусть мы имеем   случайных величин , имеющих одинаковую функцию распределения . Мы говорим, что эти случайные величины независимы в совокупности, если для любого набора пар 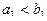, ,..., , где   и   могут быть равны также  и ,

При таком предположении условная вероятность того, что, например, , при условии, что , , , равна безусловной вероятности того, что , т. е. вероятности, вычисляемой без задания указанногоусловия:

(Вертикальная черта в этой формуле указывает на то, что первая вероятность — условная; справа от вертикальной черты записано условие, при котором вычисляется эта вероятность.) Иначе говоря, на распределение вероятности случайной величины   не влияет информация о значениях случайных величин . И вообще, на распределение вероятностей случайной величины   не влияет информация о значениях случайных величин  с .

Если случайные величины  имеют одинаковое распределение  (заданное или функцией распределения или функцией плотности) и независимы в совокупности, то часто это обозначают в записи следующим образом:

~ .

Возвращаясь к модели наблюдений

и предполагая, что  — независимые случайные величины, имеющие одинаковое распределение (i. i. d), мы должны теперь сделать еще и предположение о том, каким именно является это одинаковое для всех   распределение.