
Оценкой наименьших квадратов для параметра 
 является
является  , так что
, так что  , и
, и

Таким образом, выборочная дисперсия 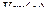 переменной
переменной  , получаемая делением
, получаемая делением  именно на
именно на  (а не на
(а не на  ), является несмещенной оценкой для
), является несмещенной оценкой для  в модели случайной выборки из нормального распределения, имеющего дисперсию
в модели случайной выборки из нормального распределения, имеющего дисперсию  . Этим и объясняется сделанный нами выбор нормировки при определении выборочных дисперсий и ковариаций.
. Этим и объясняется сделанный нами выбор нормировки при определении выборочных дисперсий и ковариаций.
При выполнении стандартных предположений отношение

имеет стандартное распределение, называемое распределением хи-квадрат с (n-p) степенями свободы. Такое же распределение имеет сумма квадратов  случайных величин, независимых в совокупности и имеющих одинаковое стандартное нормальное распределение. При
случайных величин, независимых в совокупности и имеющих одинаковое стандартное нормальное распределение. При 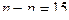 график функции плотности этого распределения имеет вид
график функции плотности этого распределения имеет вид
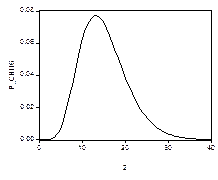
Для обозначения распределения хи-квадрат с K степенями свободы используют символ c2(K).
Итак, мы не знаем истинного значения  и поэтому в попытке построить доверительный интервал для
и поэтому в попытке построить доверительный интервал для  вынуждены заменить неизвестное нам значение
вынуждены заменить неизвестное нам значение  на его несмещенную оценку
на его несмещенную оценку

Соответственно, вместо отношения

приходится использовать отношение

Однако последнее отношение как случайная величина уже не имеет стандартного нормального распределения, поскольку в знаменателе теперь стоит не постоянная, а случайная величина.
Тем не менее, распределение последнего отношения также относят к стандартным, и оно известно под названием t-распределения Стьюдента с (n-p) степенями свободы.
Для распределения Стьюдента с K степенями свободы принято обозначение t (K). Квантиль уровня р такого распределения будем обозначать символом tp (K). График функции плотности распределения Стьюдента симметричен относительно нуля и похож на график функции плотности нормального распределения. Например, при K= 10 он имеет следующий вид (левый график).


Для сравнения, справа приведен график функции стандартного нормального распределения. Отличие графиков столь невелико, что визуально они почти неразличимы. Квантили этих двух распределений различаются более ощутимо:
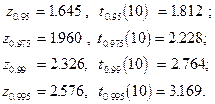
Распределение Стьюдента имеет более тяжелые хвосты. Из приведенных значений квантилей следует, например, что случайная величина, имеющая стандартное нормальное распределение, может превысить значение 1.645 лишь с вероятностью 0.05. В то же самое время, с такой же вероятностью 0.05 случайная величина, имеющая распределение Стьюдента с 10 степенями свободы, принимает значения, большие, чем 1.812.
Впрочем, для значений  квантили распределения Стьюдента
квантили распределения Стьюдента  практически совпадают с соответствующими квантилями cтандартного нормального распределения
практически совпадают с соответствующими квантилями cтандартного нормального распределения  .
.
Итак,
 ~
~  .
.
Поэтому для этой случайной величины выполняется соотношение

так что с вероятностью, равной  , выполняется двойное неравенство
, выполняется двойное неравенство

т. е.

Иными словами, с вероятностью, равной 1-a,случайный интервал
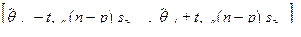
накрывает истинное значение коэффициента q j, т. е. является 95 %- доверительным интервалом для q j в случае, когда не известно истинное значение s 2 дисперсии случайных ошибок  . В среднем, длина такого интервала больше, чем длина доверительного интервала с тем же уровнем доверия, построенного при известном значении
. В среднем, длина такого интервала больше, чем длина доверительного интервала с тем же уровнем доверия, построенного при известном значении  .
.
Замечание. Выбор конкретного значения  определяет компромисс между желанием получить более короткий доверительный интервал и желанием обеспечить более высокий уровень доверия.
определяет компромисс между желанием получить более короткий доверительный интервал и желанием обеспечить более высокий уровень доверия.
Попытка повысить уровень доверия  , выраженная в выборе меньшего значения
, выраженная в выборе меньшего значения  , приводит к квантили
, приводит к квантили  с более высоким значением
с более высоким значением  , т. е. к большему значению
, т. е. к большему значению  . Но длина доверительного интервала пропорциональна
. Но длина доверительного интервала пропорциональна  . Следовательно, увеличение уровня доверия сопровождается увеличением ширины доверительного интервала (при тех же статистических данных).
. Следовательно, увеличение уровня доверия сопровождается увеличением ширины доверительного интервала (при тех же статистических данных).
Так, для  можно приближенно считать, что
можно приближенно считать, что
 ,
,
где  — квантиль уровня
— квантиль уровня  стандартного нормального распределения. Соответственно, выбирая уровень доверия
стандартного нормального распределения. Соответственно, выбирая уровень доверия  равным
равным 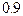 ,
, 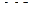 или
или  , мы получаем для
, мы получаем для  значения, приблизительно равные
значения, приблизительно равные 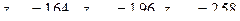 . Это означает, что переход от уровня доверия
. Это означает, что переход от уровня доверия 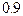 к уровню доверия
к уровню доверия 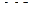 сопровождается увеличением длины доверительного интервала приблизительно в
сопровождается увеличением длины доверительного интервала приблизительно в  раза, а дополнительное повышение уровня доверия до
раза, а дополнительное повышение уровня доверия до  увеличивает длину доверительного интервала еще примерно в
увеличивает длину доверительного интервала еще примерно в  раза.
раза.
Теперь мы в состоянии перейти к построению интервальных оценок параметров моделей линейной регрессии для различного рода социально-экономических факторов на основании соответствующих статистических данных.
Пример. Вернемся к модели зависимости уровня безработицы среди белого населения США от уровня безработицы среди цветного населения. Запишем линейную модель наблюдений в виде

Получаем: 
 =
=  . Коэффициент
. Коэффициент 
 оценивается величиной
оценивается величиной  дисперсия
дисперсия  оценивается величиной
оценивается величиной  . Для построения
. Для построения  — доверительного интервала для
— доверительного интервала для  остается найти квантиль уровня
остается найти квантиль уровня  распределения Стьюдента с
распределения Стьюдента с  степенями свободы. Используя, например, Таблицу А.2 из книги Доугерти (стр.368), находим:
степенями свободы. Используя, например, Таблицу А.2 из книги Доугерти (стр.368), находим:  . Соответственно, получаем
. Соответственно, получаем  -доверительный интервал для
-доверительный интервал для  в виде
в виде

т. е.

Для  имеем
имеем  ,
,  ;
;  -доверительный интервал для
-доверительный интервал для  имеет вид
имеет вид

т. е.

В связи с этим примером, отметим два обстоятельства.
(а) Доверительный интервал для коэффициента  допускает как положительные, так и отрицательные значения этого коэффициента.
допускает как положительные, так и отрицательные значения этого коэффициента.
(б) Каждый из двух построенных интервалов имеет уровень доверия 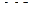 ; однако это не означает, что с той же вероятностью
; однако это не означает, что с той же вероятностью 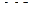 сразу оба интервала накрывают истинные значения параметров
сразу оба интервала накрывают истинные значения параметров  ,
, 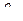 .
.
Справиться с первым затруднением в данном примере можно, понизивуровень доверия до  . В этом случае в выражении для доверительного интервала квантиль
. В этом случае в выражении для доверительного интервала квантиль  заменяется на квантиль
заменяется на квантиль  , так что левая граница доверительного интервала для
, так что левая граница доверительного интервала для 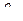 становится положительной и равной
становится положительной и равной  . Однако это достигается ценой того, что новый доверительный интервал будет накрывать истинное значение параметра
. Однако это достигается ценой того, что новый доверительный интервал будет накрывать истинное значение параметра 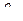 в среднем только в 90 случаев из 100, а не в 95 из100 случаев.
в среднем только в 90 случаев из 100, а не в 95 из100 случаев.
Что касается второго затруднения, то наиболее простой путь взятия под контроль вероятности одновременного накрытия доверительными интервалами для  ,
, 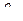 истинных значений этих параметров связан с тем, что
истинных значений этих параметров связан с тем, что
 оба интервала накрывают
оба интервала накрывают  и
и 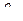 , соответственно
, соответственно 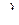 =
=
 хотя бы один из них не накрывает соответствующее
хотя бы один из них не накрывает соответствующее  =
=
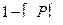 доверительный интервал для
доверительный интервал для  не накрывает
не накрывает 
 +
+
 доверительный интервал для
доверительный интервал для 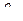 не накрывает
не накрывает 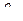
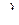 -
-
 оба интервала не накрывают свои
оба интервала не накрывают свои 
 =
=

 оба интервала не накрывают свои
оба интервала не накрывают свои 
 ³
³

Следовательно, если построить доверительный интервал для  и доверительный интервал для
и доверительный интервал для 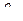 с уровнями доверия каждого, равными
с уровнями доверия каждого, равными  , то тогда правая часть полученной цепочки соотношений будет равна
, то тогда правая часть полученной цепочки соотношений будет равна 
Это означает, что в нашем примере мы можем гарантировать, что вероятность одновременного накрытия истинных значений  ,
, 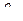 соответствующими доверительными интервалами будет не менее
соответствующими доверительными интервалами будет не менее 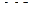 , если возьмем
, если возьмем  . Но тогда при построении этих интервалов придется использовать вместо значения
. Но тогда при построении этих интервалов придется использовать вместо значения

значение
 ,
,
так что каждый из исходных интервалов увеличится в  раза. Это, конечно, приводит к еще более неопределенным выводам относительно истинных значений параметров
раза. Это, конечно, приводит к еще более неопределенным выводам относительно истинных значений параметров  ,
, 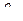 .
.
2.7. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
О ЗНАЧЕНИЯХ КОЭФФИЦИЕНТОВ
В только что рассмотренном примере мы построили  — доверительный интервал для параметра
— доверительный интервал для параметра 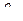 в виде
в виде

т. е.

Существенно, что при любом истинном значении параметра 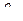 вероятность накрытия этого значения построенным доверительным интервалом равна
вероятность накрытия этого значения построенным доверительным интервалом равна 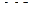 .
.
Рассмотрим значение  ; построенный интервал его не накрывает. Однако если
; построенный интервал его не накрывает. Однако если 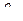 действительно равняется 1, то вероятность такого ненакрытия равна
действительно равняется 1, то вероятность такого ненакрытия равна  . Таким образом, факт ненакрытия значения
. Таким образом, факт ненакрытия значения  построенным интервалом представляет (в случае, когда
построенным интервалом представляет (в случае, когда  ) осуществление довольно редкого события, имеющего малую вероятность
) осуществление довольно редкого события, имеющего малую вероятность  , и это дает нам основания сомневаться в том, что в действительности
, и это дает нам основания сомневаться в том, что в действительности  .
.
То же самое относится и к любому другому фиксированному значению  , не принадлежащему указанному
, не принадлежащему указанному  -доверительному интервалу: предположение о том, что в действительности
-доверительному интервалу: предположение о том, что в действительности  , представляется маловероятным.
, представляется маловероятным.
Подобного рода предположения называют в этом контексте статистическими гипотезами (statistical hypothesis). О проверяемой гипотезе говорят как об исходной — «нулевой» (maintained, null) гипотезе
и обозначают такую гипотезу символом  , так что в последнем случае мы имеем дело с гипотезой
, так что в последнем случае мы имеем дело с гипотезой

В соответствии со сказанным выше, такую гипотезу естественно отвергать (отклонять), если значение  не принадлежит
не принадлежит  -доверительному интервалу для
-доверительному интервалу для 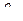 , т. е. интервалу
, т. е. интервалу
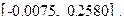
Вспоминая, как этот интервал строился, мы замечаем, что  непринадлежит этому интервалу тогда и только тогда, когда
непринадлежит этому интервалу тогда и только тогда, когда

т. е. когда наблюдаемое значение отношения

«слишком велико» по абсолютной величине. Последнее означает «слишком большое» отклонение оценки  от гипотетического значения
от гипотетического значения  параметра
параметра 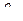 , в сравнении с оценкой
, в сравнении с оценкой  значения
значения  корня из дисперсии оценки этого параметра.
корня из дисперсии оценки этого параметра.
Итак, если

мы отвергаем гипотезу  . Однако выполнение этого неравенства для некоторого значения
. Однако выполнение этого неравенства для некоторого значения  вовсе не означает, что гипотеза
вовсе не означает, что гипотеза  обязательно не верна. Если в действительности
обязательно не верна. Если в действительности  , то все же имеется вероятность
, то все же имеется вероятность  того, что это неравенство будет выполнено.
того, что это неравенство будет выполнено.
В последнем случае, в соответствии с выбранным правилом, мы все же отвергнем гипотезу  , допустив при этом «ошибку 1-го рода». Такая ошибка происходит в среднем в
, допустив при этом «ошибку 1-го рода». Такая ошибка происходит в среднем в  случаях из ста.
случаях из ста.
Если бы мы выбрали произвольный доверительный уровень  , то тогда мы отвергали бы гипотезу
, то тогда мы отвергали бы гипотезу  при выполнении неравенства
при выполнении неравенства

и ошибка 1-го рода происходила в среднем в 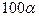 случаев из
случаев из  . Точнее, вероятность ошибки 1-го рода была бы равна
. Точнее, вероятность ошибки 1-го рода была бы равна  :
:
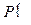
 отвергается
отвергается 
 верна
верна 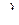 =
=  .
.
Само правило решения вопроса об отклонении или неотклонении статистической гипотезы  называется статистическим критерием проверки гипотезы Н 0, а выбранное при формулировании этого правила значение a называется уровнем значимости критерия.
называется статистическим критерием проверки гипотезы Н 0, а выбранное при формулировании этого правила значение a называется уровнем значимости критерия.
Выбор большего или меньшего значения a определяется степенью значимости для исследователя исходной гипотезы  . Скажем, выбор между значениями
. Скажем, выбор между значениями  и
и  в пользу
в пользу  означает, что исследователь заранее настроен в пользу гипотезы
означает, что исследователь заранее настроен в пользу гипотезы  и ему требуются очень весомые аргументы, свидетельствующие против этой гипотезы, чтобы все же отказаться от нее. Выбор же в пользу уровня значимости
и ему требуются очень весомые аргументы, свидетельствующие против этой гипотезы, чтобы все же отказаться от нее. Выбор же в пользу уровня значимости  означает, что исследователь не столь сильно отстаивает гипотезу
означает, что исследователь не столь сильно отстаивает гипотезу  и готов отказаться от нее и при менее убедительной аргументации против этой гипотезы.
и готов отказаться от нее и при менее убедительной аргументации против этой гипотезы.
Всякий статистический критерий основывается на использовании той или иной статистики(статистики критерия), т. е. случайной величины, значения которой могут быть вычислены (по крайней мере, теоретически) на основании имеющихся статистических данных и распределение которой известно (хотя бы приближенно).
В нашем примере критерий проверки гипотезы  основывался на использовании t-статистики
основывался на использовании t-статистики
 ,
,
значение которой можно вычислить по данным наблюдений, поскольку  — известное (заданное) число, а
— известное (заданное) число, а  и
и 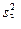 вычисляются на основании данных наблюдений.
вычисляются на основании данных наблюдений.
 2020-01-15
2020-01-15 118
118








