Упрощённый метод Ньютона

Заменим в расчётных формулах метода Ньютона (2.4), (2.5) матрицу , зависящую от , постоянной матрицы . В результате получим расчётные формулы упрощённого метода Ньютона:

,                                    (3.1)

.                                      (3.2)

Этот метод сходится со скоростью геометрической прогрессии, если начальное приближение  выбрано достаточно близким к решению , причём знаменатель прогрессии  тем меньше, чем ближе  к .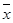

По сравнению с методом Ньютона число итераций, необходимое для достижения заданной точности , существенно возрастает. Тем не менее общие вычислительные затраты могут оказаться меньше. Причины этого состоят в следующем. Во-первых, вычисление матрицы Якоби производится здесь только один раз; во-вторых при использовании упрощённого метода Ньютона (3.1), (3.2) многократно решается система линейных уравнений с фиксированной матрицей  и различными правыми частями. Это означает, что при решении систем (3.1) методом Гаусса возможно применение LU – разложения матрицы , которое резко уменьшает число операций, необходимых для вычисления .