ВВЕДЕНИЕ.
В связи с развитием новой вычислительной техники инженерная практика наших дней все чаще и чаще встречается с математическими задачами, точное решение которых получить весьма сложно или невозможно. В этих случаях обычно прибегают к тем или иным приближенным вычислениям. Вот почему приближенные и численные методы математического анализа получили за последние годы широкое развитие и приобрели исключительно важное значение.
В данной курсовой работе рассматривается знаменитый метод Ньютона и его модификация решения систем нелинейных уравнений. Решение систем нелинейных уравнений – одна из трудных задач вычислительной математики. Трудность состоит в том, чтобы определить: имеет ли система решение, и, если – да, то сколько. Изучается сходимость основного и упрощенного методов Ньютона и метода, получаемого из метода Ньютона применением итерационного процесса для приближенного обращения матриц Якоби.
А так же коротко описываются: методы ложного положения, метод секущих, метод Стеффенсена, который чаще оказывается лучшим выбором для решения систем нелинейных уравнений нежели метод секущих или метод ложного положения.
МЕТОД НЬЮТОНА И ЕГО РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Знаменитый метод Ньютона является одним из наиболее эффективных методов решения самых разных нелинейных задач. Расчётную формулу метода можно получить, используя различные подходы. Рассмотрим два из них.
1) Метод касательных.
Выведем расчётную формулу метода для решения нелинейного уравнения  из простых геометрических соображений. Пусть
из простых геометрических соображений. Пусть 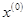 - заданное начальное приближение к корню
- заданное начальное приближение к корню  . В точке
. В точке 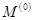 с координатами
с координатами  проведём касательную к графику функции
проведём касательную к графику функции  и за новое приближение
и за новое приближение  примем абсциссу точки пересечения этой касательной с осью
примем абсциссу точки пересечения этой касательной с осью  . Аналогично за приближение
. Аналогично за приближение  примем абсциссу точки пересечения с осью
примем абсциссу точки пересечения с осью  касательной, проведённой к графику в точке
касательной, проведённой к графику в точке  с координатами
с координатами  . Продолжая этот процесс далее, получим последовательность
. Продолжая этот процесс далее, получим последовательность  приближённой к корню
приближённой к корню  .
.
Уравнение касательной, проведённой к графику функции  в точке
в точке  имеет вид:
имеет вид:
 . (1.1)
. (1.1)
Полагая в равенстве (1.1)  , замечаем, что при выполнении условия
, замечаем, что при выполнении условия  абсцисса
абсцисса  точки пересечения касательной с осью
точки пересечения касательной с осью  удовлетворяет равенству:
удовлетворяет равенству:
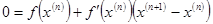 . (1.2)
. (1.2)
Выражая из него  , получаем расчётную формулу метода Ньютона:
, получаем расчётную формулу метода Ньютона:
 ,
,  . (1.3)
. (1.3)
Благодаря такой геометрической интерпретации этот метод часто называют методом касательных.
 2020-01-15
2020-01-15 171
171







