Динамічні метрологічні характеристики вимірювання тиску

 

Для вимірювального перетворювача вологості використаємо диференціальне рівняння (4.13)

 

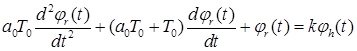 (4.13)

 

де: - масштабний множник

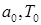- параметри які визначаються експерементально

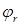 - значення вологості

Приймемо вихідну величину  як одиничну функцію (функцію Хевісайда), отримаємо рівняння виду:

 

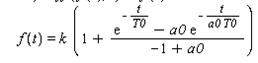 (4.14)

 

Побудуємо графік залежності вихідної величини від часу (рисунок 4.1).

 

Рисунок 4.1 - Графік залежності вихідної величини від одиничної функції

 

Приймемо вхідну величину  як імпульсну функцію , тобто функцію Дірака, отримаємо розв’язок:

 

 (4.15)

 

Побудуємо графік залежності вихідної величини від часу рисунок 4.2

Рисунок 4.2 – Графік залежності вихідної величини від часу

 

Знаходження амплітудно частотної характеристики (АЧХ) та фазочастотної характеристики (ФЧХ).

Під час аналізу диференційних рівнянь зручно користуватися представленням сигналу у вигляді перетворення Лапласа. Скориставшись усіма правилами перетворення отримаємо рівняння. Поділивши вихідний сигнал на вхідний визначимо передатну функцію

 

, (4.16)

 

Для розрахунку АЧХ і ФЧХ зробимо заміну 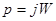, щоб надалі можна була розділити дійсну та уявну частини.

 

 , (4.17)

 

Оскільки  а для побудови графіків краще задатись частотою то проведемо і таку заміну:

 

, (4.18)

 

Виділимо дійсну та уявну частини рівняння.

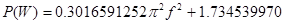, (4.19)

. (4.20)

 

Знайдемо АЧХ і ФЧХ за формулами:

 

, (4.21)

 , (4.22)

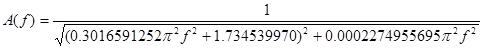, (4.23)

. (4.24)

 

 

Рисунок 4.3 – Амплітудно частотна характеристика

 

 

Рисунок 4.4 – Фазочастотна характеристика