Система образующих. Конечное число образующих

Однако не всякая группа имеет один образующий элемент. Есть группы, которые порождаются не одним, а с необходимостью несколькими (иногда бесконечным числом) элементами; и понятию одного образующего элемента приходит на смену понятие системы образующих. Очевидно, совокупность всех элементов какой-нибудь группы есть (тривиальная) система образующих этой группы.

Определение 1

Некоторое множество E элементов группы G называется системой образующих этой группы, если всякий элемент группы G есть произведение конечного числа сомножителей, каждый из которых либо есть элемент множества E, либо является обратным некоторому элементу множества E. [10]

Или говорят, что группа G порождается своим подмножеством E или что E — система порождающих (элементов) группы G, если G = { E }.

Примеры

Рассмотрим плоскость с выбранной на ней системой декартовых координат. Обозначим через G множество тех точек Р = (х, у), обе координаты которых х и у — целые числа. Установим следующее правило сложения точек: суммой двух точек Р ₁ = (x ₁, y ₁) и Р ₂ = (х ₂, у ₂) называется точка Р ₃ = (х ₃, у ₃) с координатами х ₃ = х ₁ + х ₂ и y ₃ = y ₁ + y ₂. Можно легко убедится, что это определение сложения превращает множество G в коммутативную группу и что точки (0, 1) и (1; 0) составляют систему образующих этой группы[11].

Замечание

Всякая группа имеет систему образующих.

Теорема

Множество E тогда и только тогда будет системой образующих группы G, если всякий элемент из G может быть записан хотя бы одним способом в виде произведения числа степеней элементов из E.

Определение 2

Если группа G обладает системой образующих, состоящей из конечного числа элементов, то G называется группой с конечным числом образующих.

Примеры

1. Циклическая группа — группа с одной образующей.

2. Группа 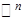 всех n -мерных векторов с целочисленными координатами с операцией сложения имеет стандартную систему образующих e = , где — вектор, у которого единственная ненулевая координата — i -ая, равная 1.

3. Система {3,7} — является системой образующих группы .

Замечание 1

Всякая система образующих группы с конечным числом образующих содержит конечное подмножество, являющееся неприводимой системой образующих этой группы.

Так как конечная система образующих всегда может быть сделана неприводимой путем удаления лишних элементов, то нужно лишь доказать, что при наших предположениях всякая бесконечная система образующих содержит конечное подмножество, также являющееся системой образующих для рассматриваемой группы. Пусть G есть группа с образующими а ₁, а _2,…, а_n ,

G = { а ₁, а _2,…, а_n },

и пусть М есть некоторая другая система образующих этой группы. Всякий элемент а_i, i = 1, 2…. n, записывается в виде произведения степеней конечного числа элементов из М. Выбирая для каждого а_i одну из таких записей и собирая те элементы из М, которые входят в эти записи i = 1, 2…. n, мы получим конечное подмножество М ¢ из М, порожденная которым подгруппа { М ¢} содержит все элементы а ₁, а _2,..., а_n и поэтому совпадает с G.

Заметим, что различные неприводимые системы образующих группы с конечным числом образующих могут содержать, вообще говоря, различное число элементов. Например, в циклической группе можно выбрать неприводимые системы образующих, состоящие более чем из одного элемента. Так, систему образующих для аддитивной группы целых чисел составляют, например, числа 2 и 3.

Замечание 2

Всякая бесконечная группа с конечным числом образующих является счетной.

 

Действительно, если элементы а ₁, а _2,…, а_n являются образующими для группы G, то всякий элемент этой группы может быть записан виде произведения

(вообще говоря, многими различными способами); всякое i_k есть одно из чисел 1, 2,…, n, причем возможно, что i_k = i_l при k ≠ l. Будем называть длиной этого произведения сумму абсолютных величин показателей:

h = |α₁| + |α₂| + … + |α_s|.

Легко видеть, что существует лишь конечное число произведений степеней образующих элементов а ₁, а _2, …, а_n данной длины h. Множество всех произведений степеней этих элементов будет, следовательно, суммой счетного множества, т.е. счетным, а поэтому и группа G будет не более чем счетной[12].

Существуют счетные группы, не имеющие конечных систем образующих. Примером таких групп являются числа , составляющие систему образующих для аддитивной группы рациональных чисел R.

Группы с конечным числом образующих составляют, следовательно, класс групп, промежуточный между конечными и счетными группами.

Примеры

1. Примером группы с двумя образующими служит таблица умножения группы самосовмещений равностороннего треугольника.

 

2. Знакопеременная группа А_n порождается множеством 3-циклов.

 

3. Группа поворотов С_n порождается одним поворотом t = 2p/ n. А группа диаэдра D_n — поворотом t и отражением r относительно одной из осей.[13]

 

Два важных примера систем образующих содержатся в приводимых ниже теоремах.

Подстановка, являющаяся циклом длины 2, называется транспозицией [14].

Теорема 1

Группа S_n порождается транспозициями.

Доказательство

Отметим, что каждая транспозиция обратна сама себе. Поэтому утверждение теоремы означает, что любая подстановка разлагается в произведение транспозиций.

Умножение подстановки

.

слева на транспозицию (ij) вызывает перестановку i и j в нижней строке. Такая операция также называется транспозицией. Очевидно, что путем последовательных транспозиций любую перестановку (k ₁, k ₂, …, k_п)можно привести к тривиальной: сначала, если k ₁ ¹ 1, меняем местами k ₁ и 1, ставя тем самым 1 на первое место, затем ставим 2 на второе место и т.д. Таким образом, существуют такие транспозиции t ₁, t ₂ ,…, t_n что

t_n … t ₂ t ₁s= id,

и, значит,

s = t ₁ t ₂ …t_{n .}

Теорема 2

Группа QL_n (K) порождается элементарными матрицами [15].

Доказательство

Отметим, что матрица, обратная к элементарной, также элементарна. Поэтому утверждение теоремы означает, что любая невырожденная матрица разлагается в произведение элементарных матриц.

Умножение матрицы А Î GL_n(K) слева на элементарную матрицу вызывает соответствующее элементарное преобразование ее строк. Мы знаем, что с помощью элементарных преобразований строк любую невырожденную матрицу можно привести к единичной матрице. Таким образом, существуют такие элементарные матрицы U₁, U₂,..., U_s,что

U_s…U₂ U₁ A = Е,

и, значит,

A = U₁ ^–1 U₂ ^–1… U_S ^–1.[16]