Пусть а — произвольный элемент группы G. Умножим его на себя, т.е. возьмем элемент а ∙ а. Этот элемент обозначим через а 2. Точно так же обозначим а ∙ а ∙ а через а 3 и вообще положим а ∙ а ∙…∙ а = аn.
Рассмотрим далее, элемент а –1 и обозначим последовательно
а –1∙ а –1 через а –2
а –1∙ а –1∙ а –1 через а –3
а –1∙ а –1∙…∙ а –1 через а – n.
Обозначения эти оправданы тем, что, действительно,
аn ∙ а –n = 1.
Для доказательства последнего утверждения заметим прежде всего, что в случае п = 1 оно очевидно (следует из самого определения а –1). Предположим, что оно верно для п –1 и докажем в этом предположении его справедливость для п. Имеем
аn ∙ а –n = (аn ∙ а n–1) (а –(n–1)∙ а –1) = а ∙{ а n–1∙ а –(n–1)}∙ а –1.
Но в силу нашего предположения фигурная скобка равна единице, значит,
аn ∙ а –n = а ∙1∙ а –1 = 1.
что и требовалось доказать.
Мы определили выражение аn для любого положительного и для любого отрицательного значения п. Положим, наконец, что, по определению, а 0 = 1.
Пусть теперь р и q — два целых числа. Из наших определений следует, что для любых целых р и q имеем
ар ∙ аq = ар + q .
Мы получаем следующий результат.
Множество Н (а) тех элементов группы G, которые могут быть представлены в виде а п при целом п с той групповой операцией, которая задана в группе G, образует группу Н (а).
В самом деле: 1) произведение двух элементов, принадлежащих Н (а), есть опять элемент Н (а); 2) единица принадлежит Н (а); 3) к каждому элементу а m из Н (а) найдется элемент а–m, который также принадлежит Н (а).
Итак, Н (а) есть подгруппа G. Эта подгруппа называется циклической подгруппой группы G, порожденной элементом а. [18]
Определение
Если любой элемент группы выражается в виде степени единственной образующей, то группа называется циклической.
Примеры
1. Примером циклической группы может служить группа вращений правильного многоугольника. Пусть дан правильный n -угольник A 1 A2...An,и пусть О — его центр. Рассмотрим всевозможные повороты плоскости вокруг точки О, при которых этот n -угольник совмещается сам с собой. Таких поворотов, очевидно, п:
a 0 —поворот на Ð 0 (тождественное преобразование),
a 1— поворот на 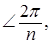
a 2— поворот на 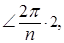
…………………
an –1— поворот на  .
.
По определению, умножение поворотов — это их последовательное выполнение одного за другим:
ak ◦ ai = ak+I,
при этом естественно считать, что ak+n = ak для любого k, в частности, ап = а 0. Это умножение, очевидно, ассоциативна (и коммутативно). Поворот а 0является единичным элементов группы и ak –1 = ап — k. для всех k = 0, 1,...., n – 1.
Если положить а 1= а,мы будем иметь а 2= а 2, а 3 = a 3, an –1 = аn– 1 и, наконец, ап = ап = а 0. Можно сказать, что эта группа образована степенями одного из своих элементов(или что она «порождается» одним из своих элементов), а именно, элемента а = а 1. Группа вращений правильного n -угольника является циклической группой порядка п;обозначается эта группа символом Сп.
2. Циклической группой порядка 3 является группа вращений треугольника. Выписав степени образующей а:
а, а 2, а 3, а 4, а 5, а 6, а 7,….
Так как а 3 = I, то эту последовательность можно переписать так:
а, а 2, I, а, а 2, I, а,….
Она представляет собой циклическое повторение основной серии а, а 2, I. Именно по этой причине данная группа — циклическая.
3. Группа целых чисел (по сложению) тоже является циклической — она порождается одним из своих элементов: ведь 2 = 1 + 1, 3 = (1 + 1)+ 1, — 1 есть элемент, противоположный к 1, и т.д. Эта группа является бесконечной циклической группой; обозначается она символом С ∞ [19].
Замечание
Обычно мы будем использовать для обозначения циклической группы букву С, а ее порядок обозначать числом в нижнем индексе. Таким образом, С 3 обозначает циклическую группу порядка 3, а Сn — циклическую группу порядка n. [20]
Таким образом, мы определили понятие циклической подгруппы Н (а), порожденной некоторым элементом а данной группы G.
Замечание
Всякая циклическая группа, коммутативна.
Доказательство
Поскольку в группе Н (а)
ар ∙ аq = ар + q = аq + p = аq ∙ ар.
то группа Н (а) коммутативна.[21]
 2020-01-14
2020-01-14 541
541








