Моделирование и идентификация парной линейной регрессии

1 2 3 4 5

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: Эконометрика

на тему: Парная линейная регрессия, парная нелинейная регрессия, множественная регрессия, временные ряды

Выполнил (а) студент (ка):

4 курса заочного отделения

Специальность: 080105.65

Финансы и кредит

Проверил (а):

Руза 2010

Содержание

1. Моделирование и идентификация парной линейной регрессии 4

1.1. План работы 4

1.2. Модель Монте-Карло линейной регрессии 4

1.2.1. Уравнение парной линейной регрессии 4

1.2.2. Последовательность выполнения работы по моделированию. 4

1.3. Идентификация модели парной линейной регрессии 9

1.3.1. Основные положения процедуры идентификации 9

1.3.2. Последовательность выполнения 10

1.4. Оценка существенности параметров линейной регрессии

и корреляции 11

1.4.1. Основные положения 11

1.4.2. Порядок выполнения проверки нулевой гипотезы 12

1.5. Оценка доверительных интервалов линии регрессии

и прогноза зависимой переменной 14

1.5.1. Основные положения 14

1.5.2. Последовательность выполнения процедуры оценки

доверительных интервалов 14

1.6. Идентификация с помощью функции «Линейн» («LINEST»)

ППП Excel 17

1.7. Идентификация с помощью «Пакета анализа - Регрессия»

ППП Excel 18

1.8. Анализ регрессии для реальных экономических показателей. 20

2. Моделирование и идентификация парной нелинейной

регрессии 22

2.1. План работы 22

2.2. Модель Монте-Карло нелинейной регрессии 22

2.2.1. Последовательность выполнения работы по моделированию 23

2.3. Идентификация модели парной нелинейной регрессии 25

2.3.1. Основные положения 25

2.3.2. Последовательность выполнения 25

2.4. Анализ нелинейной регрессии для реальных

экономических показателей 28

3. Моделирование и идентификация множественной

линейной регрессии 30

3.1. План работы 30

3.2. Модель Монте-Карло множественной линейной регрессии 30

3.2.1. Последовательность выполнения работы по моделированию 30

3.3. Идентификация модели множественной линейной регрессии 32

3.3.1. Основные положения процедуры идентификации

параметров множественной линейной регрессии 32

3.3.2. Последовательность выполнения работы 33

3.4. Идентификация с помощью «Пакета анализа - Регрессия»

ППП Excel 36

3.5. Анализ множественной регрессии для реальных

экономических показателей 38

4. Моделирование и идентификация временных рядов 41

4.1. План работы 41

4.2. Модель Монте-Карло временного ряда 41

4.2.1. Последовательность выполнения работы по моделированию 44

4.3. Идентификация модели временного ряда методом

наименьших квадратов 46

4.3.1. Основные положения идентификации 46

4.3.2. Последовательность выполнения 46

4.4. Идентификация временного ряда методом Юла-Уокера 50

4.4.1. Основные положения идентификации 50

4.4.2. Последовательность выполнения 52

4.5. Анализ временных рядов для реальных экономических

показателей. 53

Список использованной литературы 55

Моделирование и идентификация парной линейной регрессии

1.1. План работы:

- синтез модели Монте-Карло парной линейной регрессии (прямая задача).

- вычисление параметров парной линейной регрессии (обратная задача идентификации.

- оценка существенности параметров линейной регрессии и доверительные интервалы линии регрессии.

- оценка доверительных интервалов прогноза.

- идентификация модели реальных экономических наблюдений (в соответствии с заданным вариантом).

1.2. Модель Монте-Карло линейной регрессии

1.2.1. Уравнение парной линейной регрессии

Парное линейное регрессионное уравнение имеет вид

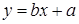, где (1.1)

x - независимая переменная (признак-фактор),

y - зависимая переменная (результативный признак),

a, b - параметры модели.

Данное уравнение определяет зависимость признак-фактора y от результативного признака x.

В реальности на данную связь оказывает влияние множество других неконтролируемых факторов, в связи, с чем данная связь представляется как:

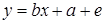, где (1.2)

e - случайное отклонение наблюдаемой зависимой переменной, вызванное влиянием других факторов. Данная величина распределена по центрированному нормальному закону со средним квадратическим отклонением σе. Задачей идентификации регрессионной модели является по данным реальных наблюдений зависимой (y) и независимой (x) переменным при наличии случайных отклонений (e) оценить параметры регрессионной модели a и b.

Именно уравнение (1.2) является основой статистического моделирования уравнения регрессии.

1.2.2. Последовательность выполнения работы по моделированию:

1.2.2.1. Открываем новую книгу. Cохраняем книгу в папке под именем ПЛР. Xls (Парная Линейная Регрессия). Озаглавим лист «Модель».

1.2.2.2. Формируем заголовки для исходных данных модели (Рисунок 1.1):

- коэффициенты модели a, b;

- объем наблюдений n;

- среднее квадратическое отклонение погрешности СКОе;

- математическое ожидание независимой переменной М_х;

-среднее квадратическое отклонение независимой переменной СКО_х.

- коэффициент корреляции r;

- коэффициент детерминации D.

Вводим n =100 и значения а, b, CKO_e (σ_е), M_x, CKO_x.

Рисунок 1.1

1.2.2.3. Сформируем заголовки таблицы модели (Рисунок 1.2).

Выделим ячейки для:

- номера наблюдения i;

- независимой переменной x;

- факторного значения зависимой переменной y, определяемой независимой переменной x;

- ошибки регрессии (отклонение наблюдаемой независимой величины от фактического значения зависимой переменной y, определяемой независимой переменной x) e;

- наблюдаемого значения зависимой переменной (с учетом ошибки регрессии e) y;

Рисунок 1.2

1.2.2.4. Сформируем заголовки строк для расчета (Рисунок 1.3) среднего, суммы, СКО соответствующих столбцов.

Рисунок 1.3

1.2.2.5. Вводим первый номер наблюдения (i=1) (Рисунок 1.3).

1.2.2.6. Смоделируем первое значение независимой переменной.

Случайное значение независимой переменной x моделируется нормальным законом распределения с заданными математическим ожиданием и средним квадратическим отклонением по формуле:

, где (1.3)

Z - центрированная и нормированная случайная величина, распределенная по нормальному закону (MZ=0, σZ=1),

M_x, σ_x - математическое ожидание и среднее квадратическое отклонение независимой переменной.

Центрированная и нормированная случайная величина моделируется на основании центральной предельной теоремы путем 12-ти кратного сложения равномерно распределенных случайных чисел R_i в диапазоне (0,1].

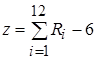(1.4)

Синтаксис функцией, возвращаемой случайное число, равномерно распределенное в диапазоне (0,1], имеет вид: R= слчис().

Таким образом, для моделирования независимой переменной необходимо в ячейку, где моделируется переменная x необходимо ввести формулу:

«=((слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()-6))* [ σ_x ] + [ M_x ]», где

[ M_x ] и [ σ_x ] - соответственно адреса ячеек, где заданы математическое ожидание и среднее квадратическое отклонение независимой переменной.

Поскольку при копировании данные адреса, где заданы математическое ожидание и среднее квадратическое отклонение не должны изменяться, ссылки на них должны быть абсолютными.

1.2.2.7. Рассчитаем теоретическое значение зависимой переменной. Теоретическое значение зависимой переменной определяется формулой:

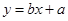, (1.5)

1.2.2.8. Смоделируем ошибку модели.

Ошибка модели моделируется центрированным нормальным законом распределения аналогично моделированию независимой переменной по формуле: «=(слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()-6)* [ σ_e ]», где

[ σ_e ] - абсолютная ссылка на ячейку, где задано среднее квадратическое отклонение ошибки регрессионной модели.

1.2.2.9. Рассчитаем фактическое значение зависимой переменной. Фактическое значение зависимой переменной рассчитывается как сумма теоретического значения и ошибки.

1.2.2.10. Моделируем сто наблюдений.

Пользуясь средствами копирования содержимого ячеек в Excel получаем 100 наблюдений независимой и зависимой переменной. В ячейку количества наблюдений n ввести 100.

1.2.2.11. Рассчитаем коэффициенты корреляции и детерминации.

В ячейку для коэффициента корреляции вводим функцию «коррел» из категории «статистические» для массивов зависимой и наблюдаемой независимой (с учетом ошибки) переменных.

Коэффициент детерминации равен:

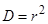, (1.6)

1.2.2.12. Рассчитаем средние, суммы и СКО:

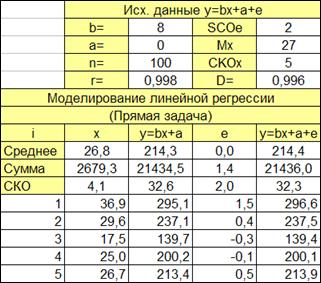
Рисунок 1.4

В соответствующие ячейки независимой переменной вводим формулы расчета среднего значения, суммы и среднего квадратического отклонения.

Скопируем данные формулы для значений зависимой (факторной, наблюдаемой) переменных и ошибки регрессии (Рисунок 1.4).

Рисунок 1.5

Представим копию интерфейса с таблицей из первых 10-ти наблюдений и двух зависимостей (Рисунок 1.5).

1.2.2.13. Исследуем влияние параметров регрессионной модели на связь y(x) Исследуем влияние СКО ошибки регрессионной модели на коэффициент корреляции и детерминации. Изменяя СКО ошибки модели получаем моделируемые значения наблюдений (Рисунок 1.6, в верхней части приведены значения коэффициентов корреляции и детерминации).

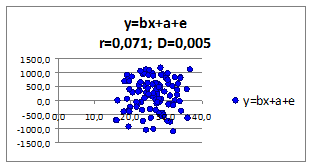
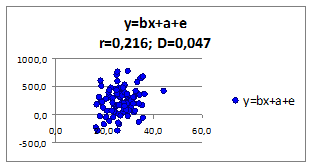
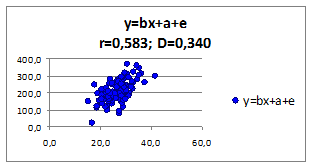
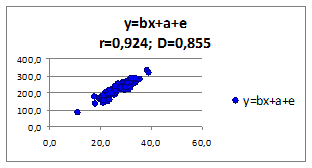
Рисунок 1.6

Исследуем влияние коэффициента регрессии b на связь зависимой переменной от независимой. Построим графики для различных коэффициентов регрессии. Значения коэффициента регрессии b приведены в верхней части рисунка:

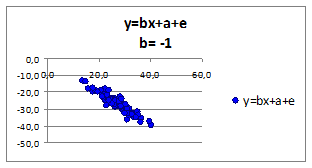
Рисунок 1.7

Исследуем влияние коэффициента а на связь зависимой переменной от независимой. Построим графики для различных коэффициентов а (а>0, а<0). Значения коэффициента регрессии a приведены в верхней части рисунка:

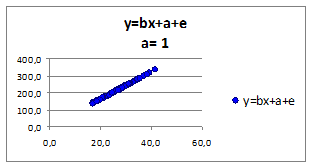
Рисунок 1.8

1.2.2.14. Сделаем выводы из полученных данных:

- знак коэффициента регрессии b имеет прямую связь со знаком коэффициента корреляции r. При изменении знака коэффициента регрессии b, меняется и знак коэффициента корреляции r.

- при уменьшении среднего квадратического отклонения σ_e, коэффициенты корреляции r и детерминации D увеличиваются.

- при изменении параметра a коэффициент эластичности не меняется.

- примеры регрессионных зависимостей в экономике с параметрами:

b>0 - зависимость средней заработной платы от среднедушевого прожиточного минимума в день одного трудоспособного человека.

b<0 - зависимость расходов на покупку продовольственных товаров (в общих расходах %) от среднедневной заработной платы одного работающего.

a>0 – зависимость расходов предприятия от объема производства.

a<0 -

1.3. Идентификация модели парной линейной регрессии

1.3.1. Основные положения процедуры идентификации:

Идентификация параметров модели основана на минимизации суммы квадратов отклонений наблюдаемой переменной от теоретической зависимости

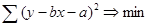(1.7)

т.е. необходимо найти такие коэффициенты a и b, которые позволяют получить наименьшее значение суммы квадратов отклонений в данном выражении. Дифференцирование данного выражения по коэффициентам a и b, приравнивание производных нулю:

(1.8)

позволяет получить систему нормальных уравнений:

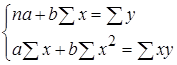(1.9)

Поделив, левые и правые части на n получаем:

(1.10)

Данный метод вычисления коэффициентов называется методом наименьших квадратов (МНК). Выражая средние значения через оператор среднего:

(1.11)

Система нормальных уравнений имеет вид:

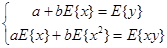(1.12)

Решение данной системы уравнений относительно a и b на основе формулы Крамера имеет вид:

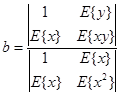(1.13)

Коэффициент a может быть получен как:

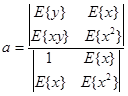(1.14)

Данный коэффициент может быть получен также по формуле, вытекающей из теоретического уравнения линейной регрессии:

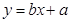, т.е. (1.15)

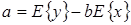(1.16)

1.3.2. Последовательность выполнения:

1.3.2.1. Создаем копию листа «Модель» помещаем его перед листом «Лист2» и переименуем его назвав «Идентификация».

1.3.2.2. Выделяем ячейки (Рисунок 1.9) для расчета:

- коэффициентов a и b,

- значений xy, x².

- значений y, полученных по рассчитанным коэффициентам a и b.

Колонки y=bx+a и e в расчете коэффициентов a и b участия не принимают, поскольку теоретическая зависимость и погрешность нам не известна. Именно их мы оцениваем по моделируемому фактическому значению y=bx+a+e.

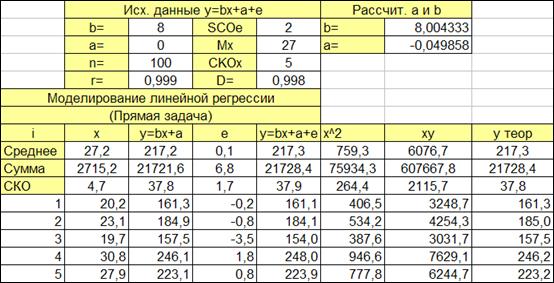
Рисунок 1.9

1.3.2.3. Рассчитаем значения xy, x².

1.3.2.4. Получим средние значения, входящие в формулы расчета коэффициентов a и b.

1.3.2.5. Рассчитаем коэффициенты a и b по формулам (1.15) и (1.16).

1.3.2.6. Сопоставим заданные коэффициенты a и b с рассчитанными.

1.3.2.7. Получим столбец идентифицированной (с рассчитанными коэффициентами линии регрессии a и b) (Рисунок 1.9).

1.3.2.8. Добавим к графику факторной линии регрессии график идентифицируемой линии (с рассчитанными коэффициентами).

1.3.2.9. Увеличивая СКО случайного отклонения σ_е получаем два графика факторной и идентифицируемой линии регрессии (Рисунок 1.10).

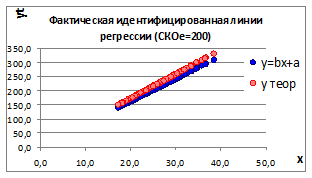
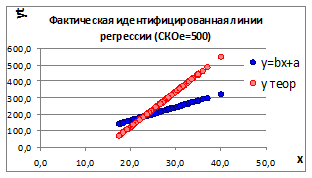
Рисунок 1.10

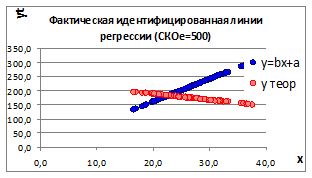
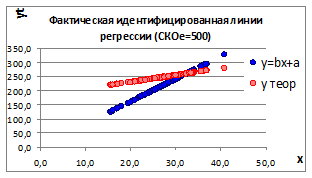
Рисунок 1.11

1.3.2.10. При увеличении СКО_е уменьшаются коэффициенты корреляции r и детерминации D, а, следовательно, уменьшается связь между изучаемыми параметрами. И это наглядно видно на графиках - несовпадение факторной и идентифицируемой линии регрессии.

1.3.2.11. Получим два наблюдения за процессом при одном и том же относительно большом СКО_е и построим графики (Рисунок 1.11).

Изменение параметров линии регрессии происходит потому, что происходит изменение влияния случайных факторов на связь между изучаемыми параметрами.

1.4. Оценка существенности параметров линейной регрессии и корреляции.

1.4.1. Основные положения:

Общая сумма квадратов отклонения независимой переменой y может быть представлена суммой квадратов отклонения y и остаточной суммы квадратов переменной

(1.17)

S_com Общая сумма квадратов отклонений

S_fact Сумма квадратов отклонений, обусловленная регрессией

S_rem Остаточная сумма квадратов отклонений

Средние квадраты данных отклонений вычисляется как:

(1.18)

(1.19)

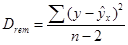(1.20)

F -отношение определяется как:

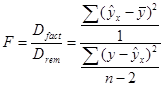(1.21)

Нулевая гипотеза (об отсутствии связи между y и x) принимается если:

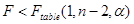, где (1.22)

F_table(1,n-2,α) - табличное значение F -критерия для степеней свободы 1 (числитель), n-2 (знаменатель), α - уровень значимости.

Гипотеза о наличии связи между y и x принимается если

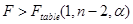(1.23)

1.4.2. Порядок выполнения проверки нулевой гипотезы:

1.4.2.1. Сделаем копию листа и озаглавим его «Существенность параметров».

1.4.2.2. Сформируем заголовки таблицы модели (Рисунок 1.12).

1.4.2.3. Выделим ячейки для расчета:

- средних квадратов отклонений на одну степень свободы (D_com, D_fact, D_rem),

- коэффициента детерминации D через суммы квадратов отклонений,

- средних квадратов отклонений,

- F -отношения, через средние квадратов отклонений на одну степень свободы,

- F -отношения, через коэффициент детерминации,

- табличного значения F -критерия,

1.4.2.4. Сформируем заголовки строк для расчета сумм квадратов отклонений.

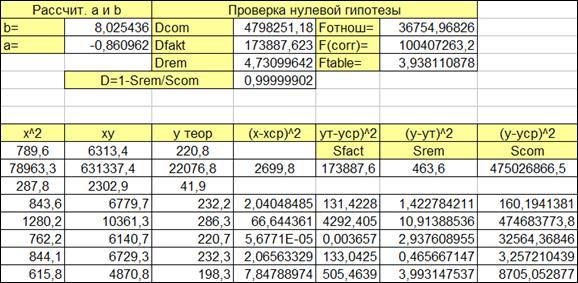
Рисунок 1.12

1.4.2.5. Рассчитаем суммы квадратов отклонений (S_fact, S_rem, S_com).

1.4.2.6. Рассчитаем средние квадраты отклонений на одну степень свободы (1.20, 1.21, 1.22).

1.4.2.7. Рассчитаем коэффициент детерминации D через суммы квадратов отклонений:

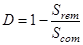(1.24)

1.4.2.8. Вычислим F -отношение через средние квадратов отклонений на одну степень свободы (1.23),

1.4.2.9. Вычислим F -отношения, через коэффициент детерминации:

1.4.2.10. Вычислим табличное значение F -критерия,

Введем табличное значение F -критерия для уровня значимости а = 0,05, воспользовавшись стандартной функцией из статистической категории F_обр (FINV) с тремя аргументами: (уровень значимости; степень свободы числителя F -отношения; степень свободы знаменателя F -отношения). Для нашего случая в ячейку табличного значения F -критерия заносится формула «=FINV(0,05;1;98)»

1.4.2.11. Из данных вычислений получили:

Так как F_table < F, то гипотеза Н_о о наличии связи между x и y принимается.

1.4.2.12. При увеличении ошибки регрессионной модели е, F -отношение уменьшается, что говорит об ослаблении связи между x и y, что, в конце концов, приводит к разрыву этой связи. Тогда гипотеза Н_о о наличии связи между x и y отвергается. (Рисунок 1.12а, Рисунок 1.12б)

Рисунок 1.12а

Рисунок 1.12б

1.4.2.13. При ошибке регрессионной модели, при которой нулевая гипотеза отвергается идентифицированная линия регрессии намного отклоняется от заданной.

1.5. Оценка доверительных интервалов линии регрессии и прогноза зависимой переменной.

1.5.1. Основные положения:

Стандартная ошибка в оценках параметров а и b определяется как:

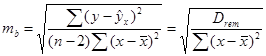(1.25)

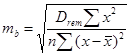(1.26)

Соответственно, доверительные интервалы для фактических коэффициентов b_f и a_f будут:

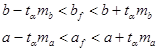(1.27)

Стандартное отклонение для линии регрессии определяется как:

(1.28)

Соответственно, доверительные интервалы для линии регрессии определяются как:

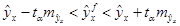(1.29)

Стандартная ошибка прогноза определяется формулой по полученной линии регрессии определяется как:

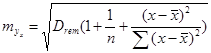(1.30)

Доверительные границы прогноза определяются как:

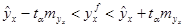(1.31)

1.5.2. Последовательность выполнения процедуры оценки доверительных интервалов:

1.5.2.1. Скопируем лист и озаглавим его «Доверительные интервалы».

1.5.2.2. Сформируем заголовки таблицы модели:

Рисунок 1.13

1.5.2.3. Выделим ячейки (Рисунок 1.13) для расчета:

- стандартных ошибок оценки коэффициента b и a (CKO_b, CKO_a),

- значения t -критерия Стьюдента для коэффициентов b и a (t_b, t_a),

- табличного значения t -критерия (tinv),

- верхних и нижних доверительных интервалов (Дов.инт. НГ, ВГ).

1.5.2.4. Рассчитаем стандартные ошибки в оценке коэффициентов линии регрессии m_b, m_a (1.27, 1.28).

1.5.2.5. Рассчитаем фактические значения t -критерия Стьюдента по формулам:

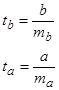(1.32)

1.5.2.6. Введем функцию расчета табличного значения t -критерия.

Аргументы функции: доверительная вероятность (α) и число степеней свободы (n-2).

1.5.2.7. Сопоставляя фактические и табличные значения t -критерия Стьюдента модели b и a и выдвинув гипотезу Н_о (о статистической незначимости параметров, т.е. a=b=rxy=0), делаем вывод:

т.к. t_a>t_табл, t_b< t_табл, то b -незначим, а не случайно отличается от нуля, а сформировалось под влиянием систематически действующей произвольной.

1.5.2.8. Рассчитаем верхние и нижние значения коэффициентов b и a для уровня значимости α=0,05 (1.29).

1.5.2.9. Добавим колонки с расчетом нижней и верхней границы линии регрессии (Рисунок 1.14).

Расчет производится по формулам (1.30, 1.31).

(При вводе формул обращаем особое внимание, на то, какие ссылки должны быть абсолютными, а какие - относительными).

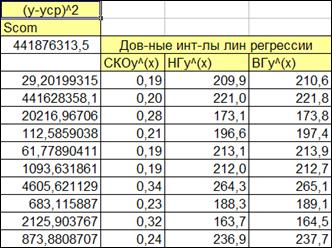
Рисунок 1.14

1.5.2.10. Построим точечные графики зависимости полученной линии регрессии и доверительных интервалов для различных значений ошибки σ_е (Рисунок 1.15).

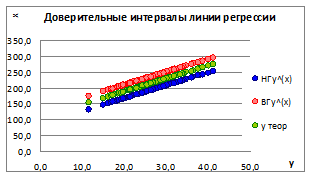
Рисунок 1.15

1.5.2.11. Как видно на графике, при увеличении значений ошибки σ_е границы доверительных интервалов увеличиваются и наоборот, что говорит об ослаблении связи между x и y.

1.5.2.12. Добавим колонки с расчетом нижней и верхней границы линии прогноза зависимой переменной для уровня значимости α=0,05 (Рисунок 1.16). Доверительные границы прогноза зависимой переменной вычисляются по формулам (1.32, 1.33).

Вначале получим столбец значений СКО (1.32). После этого получить значения нижней и верхней границ (1.33). Данные интервалы учитывают статистический характер оценок коэффициентов b и a. Однако для больших объемов наблюдений значение в формуле (1.30).

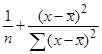
относительно малы по сравнению с единицей. В этой связи оценка стандартной ошибка прогноза может быть определена как:

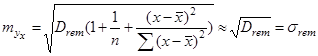(1.33)

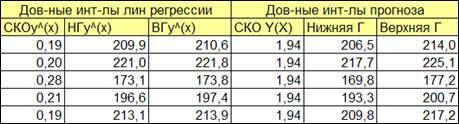
Рисунок 1.16

Доверительные интервалы в этом случае будут строиться аналогично. Однако следует учесть, что они справедливы лишь для конкретного набора зависимой и независимой переменных, т.е. для конкретных идентифицированных значений коэффициентов b и a.

1.5.2.13. Изменяя ошибку модели получим несколько доверительных границ прогноза.

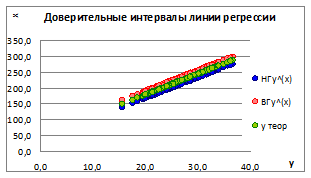
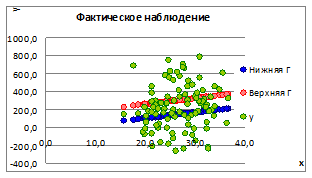
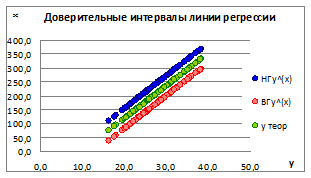
Рисунок 1.17

1.5.2.14. Из рисунка видно, что с увеличением границ прогноза связь между x и y ослабевает под влиянием ошибки σ_е. на линии регрессии.

1.6. Идентификация с помощью функции «Линейн» («LINEST») ППП Excel. Для идентификации с помощью функции «Линейн» («LINEST») ППП Excel необходимо:

-выделим массив ячеек 2х5 (Рисунок 1.18).

-вызовем функцию «линейн».

-введем 4 аргумента:

-массив y

-массив x

-константа а – ИСТИНА

-статистические характеристики – ИСТИНА

Введем данную формулу, как формулу массива для этого нажмем на клавишу F2 или активизируем строку формул. После ввода формулы массива удерживая клавиши <Shift> и <Ctrl> жмем на клавишу<Enter>.

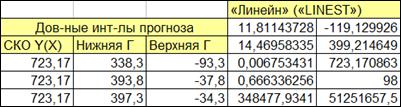
Рисунок 1.18

Таблица 1.1 представляет возвращаемые переменные в ячейках формулы массива (Рисунок 1.18).

Таблица 1.1

Коэффициент регрессии, b	Свободный член, a
СКО коэффициент регрессии b, m_b	СКО коэффициента а, m_a
Коэффициент детерминации, D	Стандартное отклонение наблюдаемых значений независимой переменной от линии регрессии, σ_rem (корень из D_rem)
F -отношение	Число степеней свободы n-2 в F -критерии (1, n-2, α)
Сумма квадратов отклонений, объясняемой регрессией	Остаточная сумма квадратов

При повторе моделирования (путем нажатия клавиши F9) полученные с данной функцией результаты совпадают с ранее вычисленными «вручную».

1.7. Идентификация с помощью «Пакета анализа - Регрессия» ППП Excel. После вызова команды «Анализ данных» в меню «Сервис» выберем инструмент анализа «Регрессия». В диалоговом окне (Рисунок 1.19) введем интервалы для независимой и зависимой переменных xy.

Введем значение уровень надежности равный (1-α)100%, где α - уровень значимости. Например, для уровня значимости α =0,05, «Уровень значимости» будет составлять 95%.

Установим флажок на «выходном интервале» и в соседнюю ссылку вставим адрес левой верхней ячейки, с которой будут выводиться результаты анализа.

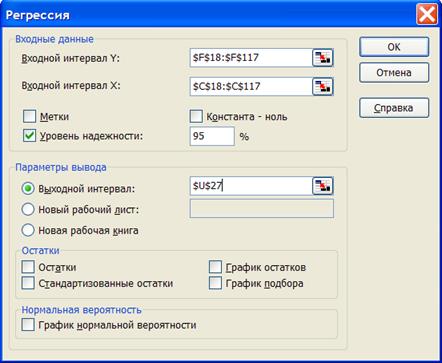
Рисунок 1.19

Рисунок 1.20 представляет результат анализа.

Заголовки таблицы «ВЫВОД ИТОГОВ».

Регрессионная статистика.

Множественный R – коэффициент корреляции, Данный пакет может быть использован для идентификации множественной регрессии (что будет рассмотрено далее), чем и объясняется определение данного коэффициента.

R-квадрат – коэффициент детерминации.

Стандартная ошибка – корень квадратный из среднего квадрата отклонений D_rem.

Наблюдения – число наблюдений.

Дисперсионный анализ

Регрессия d_f – число степеней свободы (degree of freedom) для S_fact (сумма квадратов отклонений, обусловленная регрессией).

Остаток - d_f – число степеней свободы для S_rem (остаточная сумма квадратов отклонений).

Итого - d_f – число степеней свободы для S_com (общая сумма квадратов отклонений).

Регрессия - SS –сумма квадратов отклонений, обусловленная регрессией (S_fact).

Остаток - SS –остаточная сумма квадратов отклонений (S_rem).

Итого SS –общая сумма квадратов отклонений (S_com).

Регрессия - MS – cредний квадрат отклонений на одну степень свободы, обусловленный регрессией (D_fact).

Остаток - MS – cредний квадрат отклонений на одну степень свободы, обусловленный регрессией (D_rem).

Итого - MS – cредний квадрат отклонений на одну степень свободы, обусловленный регрессией (D_com).

F – F -отношение.

Значимость F - вероятность принятия нулевой гипотезы (гипотезы об отсутствии связи).

Y-пересечение – Коэффициенты – оценка коэффициента а.

Переменная х₁ - Коэффициенты - оценка коэффициента b.

Y-пересечение (Переменная х₁, х₂) – Стандартная ошибка – СКО оценки коэффициентов а и b.

Y-пересечение (Переменная х₁, х₂) – t-статистика – фактические значения t -критерия Стьюдента для коэффициентов а и b.

Y-пересечение (Переменная х₁, х₂) - Р-значения - вероятность принятия нулевой гипотезы относительно коэффициентов регрессии а и b.

Y-пересечение (Переменная х₁, х₂) – Нижние (Верхние) 95% - Нижние и верхние доверительные границы для коэффициентов регрессии а и b для доверительной вероятности 0,95 (а=0,05).

(Экспоненциальная форма представления числа 1Е-44 эквивалентна записи 1*10-44).

1.7.1. Сопоставим значения таблицы «ВЫВОД ИТОГОВ» с рассчитанными вручную и с использованием функции «ЛИНЕЙН».

Рисунок 1.20

1.8 Анализ регрессии для реальных экономических показателей

По статистическим данным за n -ый год сформирована таблица. Проведем идентификацию и анализ парной линейной регрессии, используя функцию «Линейн» ППП Excel (Рисунок 1.21).

Рисунок 1.21

На основе данной таблицы и с помощью функции «Линейн» ППП Excel получаем следующие данные (Рисунок 1.22):

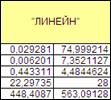
Рисунок 1.22

Из полученных данных можем вывести линейное уравнение зависимости y от x. Оно имеет вид: y =74,999214+0,029281 x, т.е. с увеличением выручки на 1 руб., зар.плата будет увеличиваться на 0,029281 в среднем.

Судя по значению D=0,443311- связь переменных регрессии умеренная. Причем, 44%- это доля вариации y, объясненная вариацией фактора x, включенного в уравнение, а остальные 56% вариаций приходятся на долю других факторов, не учтенных в уравнении.

Выдвинем гипотезу Н_о о статистически незначимом отличии показателей от нуля: a=b=r_xy=0. С помощью таблицы Стьюдента определили, что t_табл для числа степеней свободы d_f=n-2 =30-2=28 и а=0,05 составляет 2,0484.

t_a =74,999214/7,3521127=10,2> t_табл t_b =0,029281/0,006201=4,72> t_табл

Исходя из этого, гипотеза Н_о отклоняется т.е. a и b неслучайно отличаются от нуля, а статистически значимы.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: