Моделирование и идентификация парной нелинейной регрессии

2.1. План работы

В процессе выполнения данной работы необходимо:

-синтезировать модель Монте-Карло парной нелинейной регрессии (прямая задача).

-вычислить параметры парной нелинейной регрессии (обратная задача идентификации.

-оценить существенность параметров линейной регрессии и доверительные интервалы линии регрессии.

-оценить доверительные интервалы прогноза.

-составить отчет по работе.

2.2. Модель Монте-Карло нелинейной регрессии

Парная нелинейная регрессия подразделяется на два вида

-нелинейная относительно независимой переменной x,

-нелинейная относительно оцениваемых параметров a и b.

Примером первого вида являются уравнения:

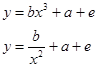                                         (2.1)

Примером второго вида являются степенная и экспоненциальная функции:

, где                                         (2.2)

x - независимая переменная (признак-фактор),

y - зависимая переменная (результативный признак),

a, b - параметры модели.

e - случайное отклонение наблюдаемой зависимой переменной, вызванное влиянием других факторов. Аналогично линейным моделям данная величина распределена по центрированному нормальному закону со средним квадратическим отклонением σ_е. Задачей идентификации регрессионной модели является по данным реальных наблюдений зависимой (y) и независимой (x) переменной при наличии случайных отклонений (e) оценить параметры регрессионной модели a и b.

Парная нелинейная регрессия относительно независимой переменной x легко приводится к линеному виду путем замены переменной (z=x3 – для первого уравнения и z=1/x2 – для второго).

                                   (2.3)

Уравнения парной нелинейной регрессия относительно оцениваемых параметров a и b не все приводятся к линейному виду. В данной работе рассматриваются модели, которые могут быть приведены к линейному виду (такие нелинейные модели называются внутренне линейными).

Степенная и экспоненциальная модели внутренне линейны, поскольку они могут быть приведены в линейному виду.

Так, для степенного уравнения логарифмирование позволяет получить линейную модель в виде:

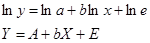                                       (2.4)

Аналогично экспоненциальная модель приводится как:

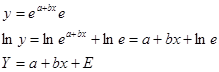                           (2.5)

Данные уравнения являются основой статистического моделирования нелинейной регрессии.

Значения параметров для выполнения работы определяется вариантом. Ниже представлена методика выполнения работы для уравнения

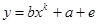                                             (2.6)

2.2.1. Последовательность выполнения работы по моделированию.

2.2.1.1. Откроем новую книгу и сохраним ее в своей папке под именем ПНР.xls (Парная Нелинейная Регрессия). Озаглавим лист «Модель».

2.2.1.2. Сформируем заголовки для исходных данных модели (Рисунок 2.1)

- коэффициенты модели a, b;

- объем наблюдений n;

- среднее квадратическое отклонение погрешности СКО_е;

- математическое ожидание независимой переменной М_х;

- среднее квадратическое отклонение независимой переменной СКО_х.

- значение степени k

2.2.1.3. Введем значения а, b, k, CKO_e (σ_е), M_x, CKO_x.

Рисунок 2.1

2.2.1.4. Сформируем заголовки таблицы модели (Рисунок 2.2).

2.2.1.5. Выделим ячейки для:

-расчета коэффициента корреляции r;

-индекса корреляции R.

-номера наблюдения i;

-независимой переменной x;

-факторного значения зависимой переменной y, определяемой независимой переменной x;

-ошибки регрессии (отклонение наблюдаемой независимой величины от фактического значения зависимой переменной y, определяемой независимой переменной x) e;

-наблюдаемого значения зависимой переменной (с учетом ошибки регрессии e) y;

Рисунок 2.2

2.2.1.6. Введем первый номер наблюдения (i=1).

2.2.1.7. Смоделируем первое значение независимой переменной.

Случайное значение независимой переменной x моделируется аналогично линейной модели.

2.2.1.8. Рассчитаем теоретическое значение зависимой переменной.

Теоретическое значение зависимой переменной определяется формулой:

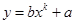                                              (2.7)

2.2.1.9. Смоделируем ошибку модели.

Ошибка модели моделируется аналогично линейной модели.

2.2.1.10. Рассчитаем фактическое значение зависимой переменной. Фактическое значение зависимой переменной рассчитывается как сумма теоретического значения и ошибки.

2.2.1.11. Смоделируем сто наблюдений.

Пользуясь средствами копирования содержимого ячеек в Excel получим 100 наблюдений независимой и зависимой переменной. В ячейку количества наблюдений n введем 100.

В отчете представить 10 первых значений (Рисунок 2.3) и построить точечные графики теоретической зависимости 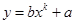и смоделированных фактических наблюдений  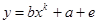(Рисунок 2.4).

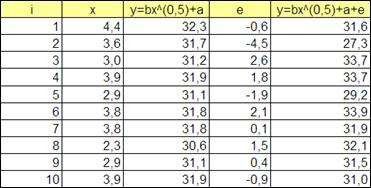
Рисунок 2.3

Рисунок 2.4

2.3. Идентификация модели парной нелинейной регрессии.

2.3.1. Основные положения:

Рассматриваемая нелинейная регрессионная модель приводится к линейной путем введения новой переменной

.

Процедура идентификации и анализа полученной линейной модели y (z) аналогичена процедуре идентификации и анализа для линейной модели.

2.3.2. Последовательность выполнения.

2.3.2.1. Вводим новую переменную.

2.3.2.2. Получим столбец 100 значений новой переменной (Рисунок 2.5).

Рисунок 2.5

Таким образом, задача свелась к линейной модели

2.3.2.3. Для определения параметров a и b применить функцию «Линейн» («LINEST») ППП Excel, для чего выделить массив ячеек 2х5 (Рисунок 2.6).

Рисунок 2.6

2.3.2.4. Аналогично, как это делалось для линейной модели вводим формулу массива.

В ячейках формулы массива (Рисунок 2.6) возвращаемые переменные расположены в соответствии с таблицей, представленной в разделе парной линейной регрессии.

2.3.2.5. Сопоставим идентифицированные значения коэффициентов модели с заданными.

Посредством нажатия на клавишу F9 (при нажатии которой происходит новая генерация случайных чисел) пронаблюдать за изменением идентифицируемой линий регрессии из-за вариации рассчитанных коэффициентов a и b.

2.3.2.6. Видно, что при увеличении коэффициента a, коэффициент b уменьшается. Идентификационная линия регрессии с уменьшением коэффициента a приближается к теоретической линий данной регрессии.

Заключение о принятии нулевой гипотезы, построение доверительных интервалов линии регрессии y (z) и прогноза строятся аналогично, как это делалось выше для линейной модели (в рамках данной работы это разрешается не проводить).

2.3.2.7. Построим точечные графики зависимости теоретической и идентифицируемой линий регрессии.

Для этого необходимо преобразовать полученные зависимости от z в зависимости от x и получить столбец значений y (Рисунок 2.7).

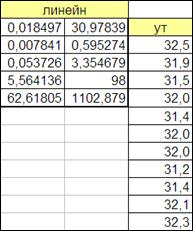
Рисунок 2.7

В качестве параметров a и b используются идентифицированные с помощью функции «Линейн» значения.

2.3.2.8. С помощью мастера диаграмм построим теоретическую и идентифицированную линии регрессии (Рисунок 2.10).

2.3.2.9. Построим доверительные интервалы прогноза.

Доверительные интервалы прогноза определяются как:

, где

- теоретическое идентифицированная нелинейная линия регрессии (на странице Excel – yт),

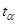- табличное значение коэффициента Стъюдента для доверительной вероятности α=0,05,

- Стандартное отклонение наблюдаемых значений независимой переменной от линии регрессии (2-й столбец,3-я строка возвращаемой таблицы функции «ЛИНЕЙН»).

Табличное значение коэффициента Стъюдента (tinv) для рассматриваемого примера (Рисунок 2.8):

Рисунок 2.8

Получим график с нелинейной регрессией и доверительными интервалами прогноза (Рисунок 2.9).

Рисунок 2.9

2.3.2.10. Генерируя различные случайные последовательности и изменяя СКО_e получим различные теоретические и идентифицированные линии регрессии (Рисунок 2.10, Рисунок 2.11).

Рисунок 2.10

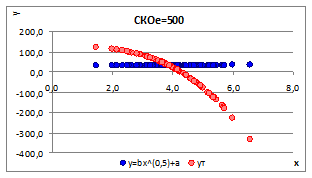
Рисунок 2.11

2.3.2.11. Из полученных линий регрессии видим, что в нашем случае (при первоначально заданной CKO_e =3) связь параметров a и b была достаточно сильной. Поэтому при генерации различных случайных последовательностей теоретические и идентифицированные линии регрессии практически не отличаются друг от друга. При увеличении CKO_e (CKO_e =500) появляются значимые различия между линиями, а в некоторых случаях связь близка к разрыву.

2.4. Анализ нелинейной регрессии для реальных экономических показателей.

Исследуем зависимость общих расходов предприятия от объема производства.

Дана таблица наблюдений:

Рисунок 2.12

Исследуем данную зависимость при заданном уравнении y= bx^k+a+e и k =0.5.

Получим средние значения по столбцам, а так же значения XY и X^2.

Вычислим значения a и b:

b= (срXY-срX*срY)/(срX^2-(срX)^2))

a=срY-b*срX.

Формула для вычисления Y_теор имеет вид: Y_теор=b*x+a.

Рассчитаем средний квадрат отклонения (Y-Y_теор)^2, а так же для приведения нелинейного уравнения к линейному введем и рассчитаем новую переменную Z=X^k.

Рисунок 2.13

При помощи функции «Линейн» проведем анализ полученных данных:

Рисунок 2.14

Графически данная зависимость имеет вид:

Рисунок 2.15