Моделирование и идентификация временных рядов

4.1. План работы

В процессе выполнения данной работы необходимо:

-синтезировать модель Монте-Карло временного ряда (прямая задача).

-вычислить параметры временного ряда (обратная задача идентификации) на основе метода наименьших квадратов и получить уравнение прогноза.

-вычислить параметры временного ряда (обратная задача идентификации) на основе процедуры Юла-Уокера и получить уравнение прогноза.

-составить отчет по работе.

4.2. Модель Монте-Карло временного ряда.

В общем виде модель авторегрессии-скользящего среднего АРСС(p,q) имеет вид:

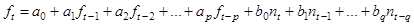, где (4.1)

f_t –значение временного ряда в момент времени t,

f _t – значение временного ряда в момент времени t-1, t-2,…,t-k,

a_i b_i – коэффициенты модели,

n_t, n_t-1,…, n_t-k – значения случайного центрированного (математическое ожидание равно нулю) и нормированного (среднее квадратическое отклонение равно единице) импульса типа «белый шум» в моменты времени t, t-1, t-2,…,t-k.

Коэффициент a₀ определяет (но не равен ему) среднее значение ряда (но не равен ему).

Анализ временных рядов удобно производить с помощью дискретного преобразования Лапласа или z -преобразования (основанным на гармоническом разложении Фурье и преобразовании Фурье). Таблица 4.1 представляет весьма простые формулы для преобразования временного ряда, представленного во временной области, в ряд в терминах z -преобразования и обратно.

Таблица 4.1.

Основная теорема z -преобразования
Описание процесса во временной области	Описание процесса во области z -преобразования

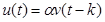
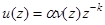
Преимущество рассмотрения временных рядов в области z -преобразования по сравнению с их анализом во временной области заключается в понижении «сложности» математических действий. Так операции дифференцирования, интегрирования, умножения, деления во временной области в z -пространстве заменяются на операции умножения, деления, сложения, вычитания, соответственно.

Значительным преимуществом представления временных рядов в z -пространстве является то, что это позволяет проводить математические действия над ними (складывать, вычитать, умножать, делить).

Без нарушения общности для простоты положим, что коэффициент a₀ равен нулю.

На основании формул в данной таблице временной ряд (4.1) в терминах z-преобразования (с учетом равенства нулю коэффициента a₀) будет выглядеть как:

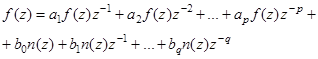                (4.2)

Преобразуя данное выражение (вынося за скобки) f(z) и n(z) получаем;

,

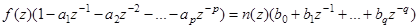Откуда:

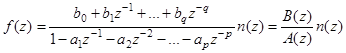
Полином:

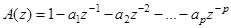                        (4.3)

определяет «авторегрессионную» составляющую модели.

Полином:

                                 (4.4)

представляет собой составляющую «скользящее среднее».

Уравнение:

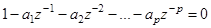                            (4.5)

называется характеристическим уравнением.

Корни данного уравнения полностью описывают поведение временного ряда. Для стационарных процессов все корни характеристического уравнения должны быть по модулю меньше единицы

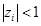
Если корни характеристического уравнения комплексно-сопряженными, то во временном ряду имеет место гармоническая составляющая.

В данной контрольной работе рассматривается модель авторегрессии 2-го порядка АРСС(2,0) или АР (2).

Соответственно модель авторегрессии 2-го порядка во временной области будет иметь вид

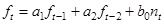,                                    (4.6)

а в z -преобразовании:

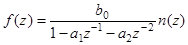                                          (4.7)

Характер временного ряда определяется корнями характеристического уравнения:

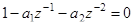                                           (4.8)

Домножим левую и правую части на z² и получим квадратное уравнение:

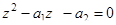                                               (4.9)

Корни характеристического уравнения определяются как:

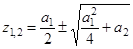                                            (4.10)

По определению корней уравнения имеем:

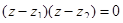                                              (4.11)

или:

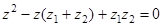                                      (4.12)

Сопоставляя данное уравнение с (4.9) находим коэффициенты модели:

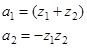                                           (4.13)

Пусть корни характеристического уравнения комплексно-сопряженные:

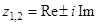, где                                   (4.14)

Re, Im – действительная и мнимая части корней характеристического уравнения, соответственно.

Тогда на основании уравнения (4.13) получаем:

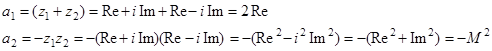, где   (4.15)

М – модуль корней характеристического уравнения

Рисунок 4.1 представляет единичный круг с комплексно-сопряженными корнями.

Для стационарного временного ряда все корни характеристического уравнения находятся внутри единичного круга (Рисунок 4.1).

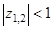                                         (4.16)

Рисунок 4.1

Из этого условия вытекают ограничения на коэффициенты а₁, а_{2 :}

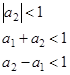                                               (4.17)

Аргумент φ определяется как:

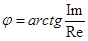                                           (4.18)

Период временного ряда определяется отношением:

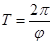                                                  (4.19)

При a₀ =0 среднее значение ряда равно нулю. При a₀ ≠0 среднее значение временного ряда определяется как:

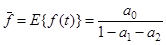                            (4.20)

Дисперсия ряда определяется как:

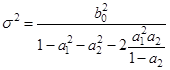                           (4.21)

Уравнение (4.6) является основой статистического моделирования временного ряда.

4.2.1. Последовательность выполнения работы по моделированию.

4.2.1.1. Откроем новую книгу и сохраним ее в своей папке под именем ВР. xls (Временной ряд). Озаглавим лист «Модель».

4.2.1.2. Сформируем заголовки для исходных данных модели (Рисунок 4.2):

-действительные, мнимые части, модуль и аргумент корней характеристического уравнения Re, Im, M, arctgφ;

-период Т;

-коэффициенты модели a0, a1, a2, b0;

-среднего значения и среднего квадратического отклонение ряда;

4.2.1.3. Введем значения Re, Im, a0, b0, соответствующие варианту контрольной работы.

4.2.1.4. Вычислим значения a1, a2, M², M, arctgφ,T (Рисунок 4.2).

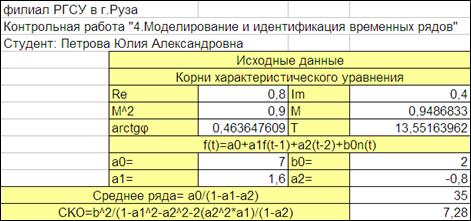
Рисунок 4.2

4.2.1.5. Сформируем заголовки таблицы модели временного ряда (Рисунок 4.3).

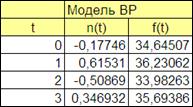
Рисунок 4.3

4.2.1.6. Введем первые 4 номера наблюдений (t =1,2,3).

4.2.1.7. Смоделируем 4 значения случайного центрированного импульса n(t).

(математическое ожидание случайного импульса Mn=0 и среднее квадратическое отклонение случайного импульса СКОn=1)

Для этого аналогично, как моделировалась погрешность в предыдущих работах, в соответствующие ячейки необходимо ввести формулу:

«=(слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()-6»

4.2.1.8. Смоделируем первые 4 значения временного ряда от математического ожидания.

В момент времени t=0 значения f(t-1) и f(t-2) не определены, а для момента времени t=1 не определено значение f(t-2). Поэтому данные значения ряда могут быть определены через средние значения (математические ожидания ряда).

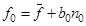
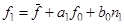                                    (4.22)

Для момента времени t=2,3,4,… предыдущие значения временного ряда определены и, следовательно, в момент времени t=2 вводится формула, которая с учетом необходимости абсолютных ссылок на коэффициенты модели имеет вид (для данного расположения таблицы и исходных данных на листе Excel): «=$D$9*D16+$D$10*D15+$D$11*C17».

Выделяя последние 2 строки (для автоматического изменения значения времени) полученной таблице копировать моделируемое значения временного ряда до момента времени t=400 (Рисунок 4.3 представляет лишь первые 4 значения).

4.2.1.9. Построить графики временного ряда f(t) (Рисунок 4.4).

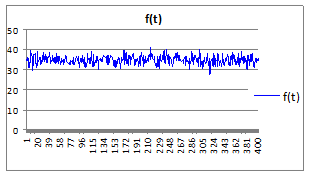
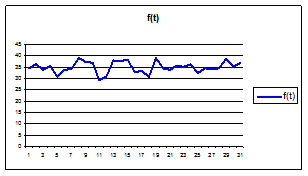
Рисунок 4.4

4.3. Идентификация модели временного ряда методом наименьших квадратов.

4.3.1. Основные положения:

Целью идентификации является оценка параметров a0, a1, a2, b0 по наблюдаемым (смоделированным) значениям, т.е. уравнению ряда:

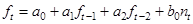                                (4.23)

можно поставить в соответствие уравнение множественной регрессии:

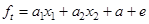, где                             (4.24)

x₁=f_t-1 , x₁=f_t-1, e=b₀n_t

В этом случае параметры a0, a1, a2 могут быть определены методом наименьших квадратов, как это проводилось при идентификации множественной регрессии.

Параметр b0 определяется на основе дисперсии временного ряда (4.21),

                            (4.25)

4.3.2. Последовательность выполнения:

4.3.2.1. Сделаем копию листа и озаглавим его «Идентификация МНК».

4.3.2.2. Добавим столбцы со значениями f(t-1) и f(t-2) (Рисунок 4.5).

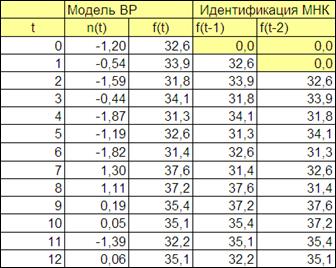
Рисунок 4.5

4.3.2.3. Проведем идентификацию методом наименьших квадратов (с помощью «Пакета анализа - Регрессия» ППП Excel)

Идентификация с помощью «Пакета анализа - Регрессия» ППП Excel аналогична процедуре идентификации множественной регрессии. В качестве входного интервала Y вводим столбец f(t), входного интервала Х – два столбца f(t-1) и f(t-2). Установим «флаг» на выходной интервал, зададим адрес пустой ячейки справа оставив 3 пустых столбца от столбца f(t-2) и нажав на клавишу ОК получим результаты идентификации(Рисунок 4.6).

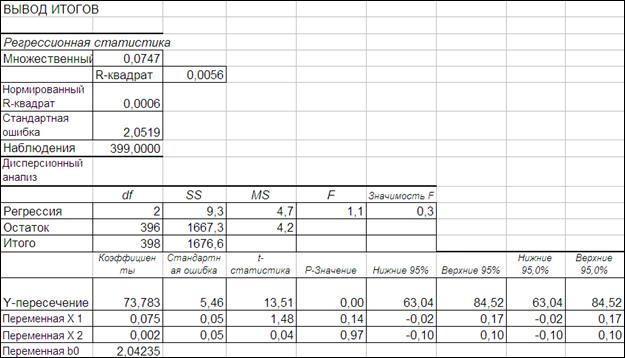
Рисунок 4.6

4.3.2.4. Оценим значение b0 по формуле 4.25.

Для этого рассчитаем среднее значение ряда и его среднее квадратическое отклонение (функции СРЗНАЧ и СТАНДОТКЛОН).

Пользуясь свойством копирования ячеек рассчитаем данные параметры для всех полученных столбцов в конце таблицы. Для удобства скопируем заголовок таблицы, и, разместить его в последней строке. Рисунок 4.7).

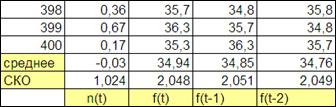
Рисунок 4.7

Под ячейкой переменная х1 таблицы ВЫВОД ИТОГОВ сформируем заголовок переменная b0 (Рисунок 4.8). В соседнюю ячейку введем формулу расчета b0.

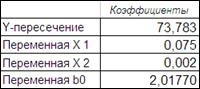
Рисунок 4.8

4.3.2.5. Оценим сущность полученной модели a0, a1, a2.

-дадим заключение о нулевой гипотезе,

-построим доверительные интервалы для коэффициентов модели a0, a1, a2

4.3.2.6. Сопоставим идентифицированные значения коэффициентов модели с заданными.

4.3.2.7. Введем столбец прогноза ряда (Рисунок 2.6), в котором прогнозируемые значения ряда в момент времени t +1 вычисляются в момент времени t по формуле:

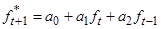, где

a0, a1, a2 - идентифицированные значения коэффициентов модели, соответственно, «Y-пересечение», «Переменная Х1», «Переменная Х2».

Для этого в ячейку f (2) введем данную формулу. При этом ссылки на ячейки со значениями a0, a1, a2 («Y-пересечение», «Переменная Х1», «Переменная Х2») должны быть абсолютными.

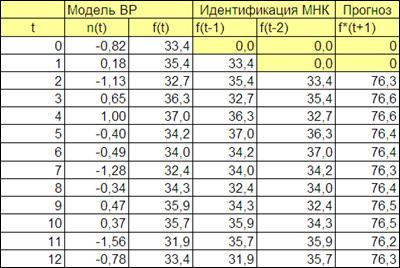
Рисунок 4.9

4.3.2.8. Построим график изменения временного ряда и прогноза для первых (начиная с момента времени t =2) 25-35 значений (Рисунок 4.10).

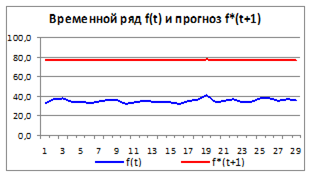
Рисунок 4.10

4.3.2.9. Получим столбец ошибок прогноза (начиная с момента времени t =2) f^*(t)-f(t).

4.3.2.10. Получим автокорреляционную функцию ошибки прогноза.

Для этого выделим ячейки для аргумента k автокорреляционной функции и самой функции r(k).

Замечание: при включенном режиме (Сервис\параметры\вычисления) Автоматически или в режиме Вручную и при нажатии клавиши F9 весь лист пересчитывается заново. В этой связи все моделируемые, а следовательно и рассчитываемые по формулам переменные изменяются.

Введем значения аргумента k (от 0 до 30) (Рисунок 2.7).

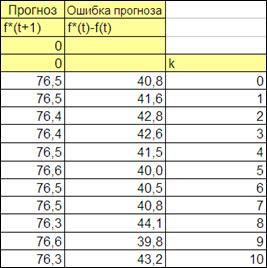
Рисунок 4.11

Для получения автокорреляционной функции в ячейку, соответствующей r(0) вставить формулу расчета коэффициента корреляции (категория статистические, функция КОРРЕЛ):

«=КОРРЕЛ(I22:I389;I22:I389)»

В качестве массива 1 и массива 2 используется один и тот же массив ошибок. Обратим внимание на то, что вводимые массивы ошибок на 30 (от t=0 до t=370) данных меньше чем полный массив моделирования (от t=0 до t=400).

Это связано с тем, что нам необходимо получить значения коэффициента корреляции между массивами f(t) и f(t+k), где k изменяется от 0 до 30. Значения же f (371+30) не существует.

После нажатия на клавишу «Ввод» получаем значение автокорреляционной функции для k=0, равное единице.

Для получения автокорреляционной функции для k=1.2,3,…30 необходимо изменять адреса второго массива последовательно на единицу,

Для этого необходимо в формуле расчета коэффициента корреляции r(0) ссылки на первый массив сделаем абсолютными, т.е. с помощью клавиши «F4» запишем как: «=КОРРЕЛ($I$22:$I$389;I22:I389)»

После этого скопируем данную формулу для всех k=1.2,3,…30 (Рисунок 4.12).

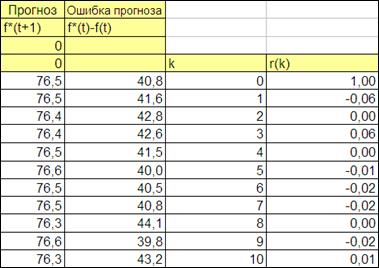
Рисунок 4.12

Получим график автокоррелфяционной функции и сделаем заключение о качестве полученной модели прогноза (Рисунок 4.13).

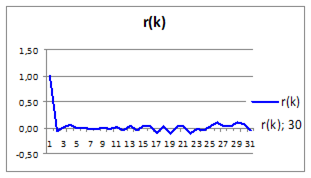
Рисунок 4.13

4.4. Идентификация временного ряда методом Юла-Уокера.

4.4.1. Основные положения идентификации:

Как было показано, модель авторегрессии АР (p) имеет вид:

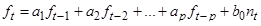                  (4.26)

Домножим левую и правую части на f(t-k):

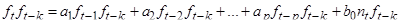
Применим оператор среднего к левой и правой частям:

.

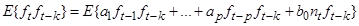Учитывая свойство линейности оператора среднего (оператор от суммы равен сумме оператором и оператор от постоянной, умноженной на случайную величину равен постоянной, умноженной на оператор от случайной величины) получаем:

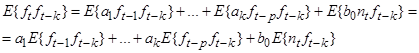
Разделив левую и правую части на дисперсию временного ряда получаем:

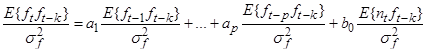
Исходя из определения коэффициента автокорреляции центрированной случайной величины:

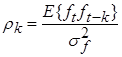
и учитывая, что коэффициент корреляции временного ряда f_t-k с белым шумом n_t равен нулю получаем:

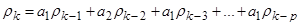                    (4.27)

Подставив в данное выражение последовательно k =1,2,3,…, p получаем систему уравнений:

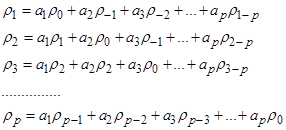
Учитывая, что

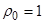
и то, что автокорреляционная функция четная

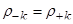
получаем:

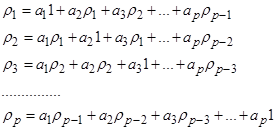
Данная система уравнений в векторной форме имеет вид:

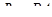, где                                   (2.28)

, ,

 

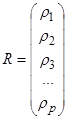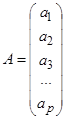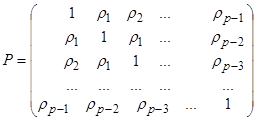
Вектор R и матрица P состоят из коэффициентов автокорреляции, которые вычисляются известным значениям временного ряда.

Вектор А, представляющий неизвестные коэффициенты модели (которые и подлежат идентификации) может быть определен из уравнения (4.28) как:

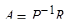
Данное уравнение носит название уравнения Юла-Уокера

4.4.2. Последовательность выполнения:

4.4.2.1. Сделаем копию листа и озаглавим его «Идентификация Юл-Уокер».

4.4.2.2. Удалим промежуточные и выходные результаты идентификации методом наименьших квадратов.

Для этого очистить ячейки с результатами идентификации МНК с помощью Пакета анализа Регрессия и восстановить свойства их границ.

Удалим четыре столбца нового листа: «прогноз f *(t +1)», «ошибка прогноза - f *(t)- f (t)», «k», «автокорреляционную функцию ошибки прогноза - r(k)».

4.4.2.3. Получим необходимые значения коэффициентов корреляции.

Вектор R и матрица R уравнения Юла-Уокера:

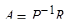
для авторегрессионной модели 2-го порядка имеют вид:

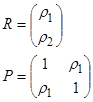
Следовательно, получим значения коэффициентов автокорреляции временного ряда ρ ₁, ρ ₂. Аналогично, как вычислялась выше автокорреляционная функция для ошибки прогнозирования, получим значения автокорреляционного ряда f(t) (Рисунок 4.14).

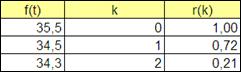
Рисунок 4.14

4.4.2.4. Сформируем вектор R и матрицу P уравнения Юла-Уокера (Рисунок 4.15)

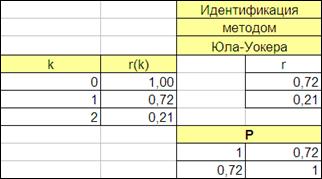
Рисунок 4.15

4.4.2.5. Получим обратную матрицу P^-1 (функция МОБР) (Рисунок 4.16).

4.4.2.6. Получим вектор А (функция МУМНОЖ) (Рисунок 4.16).

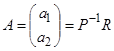
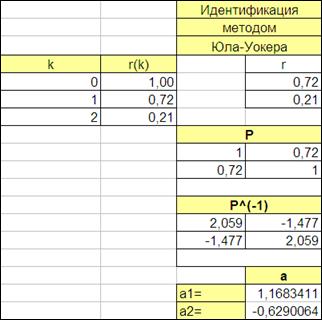
Рисунок 4.16

4.4.2.7. Сопоставим идентифицированные параметры временного ряда с заданными:

Заданные:	Идентифицированные:
a1 = 1,6	а1 = 1,16
а2 = -0,8	а2 = -0,62

4.5. Анализ временных рядов для реальных экономических показателей.

Установлена зависимость прибыли предприятия у (млн.руб.) от цен на сырье х₁ (тыс. руб. за 1т) и производительности труда х₂ (ед. продукции на 1 рабочее место). На основании наблюдений составлена таблица:

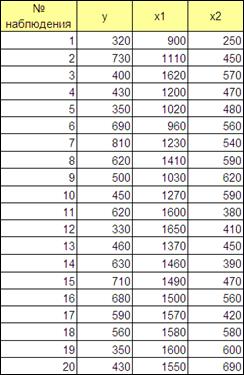
Рисунок 4.17

Проведем идентификацию с помощью «Пакета анализа - Регрессия» ППП Excel.

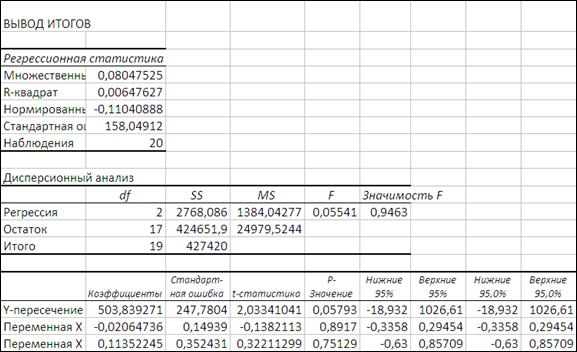
Рисунок 4.18

Из полученных данных видим, R -квадрат свидетельствует о невысокой точности данной модели. Хотя множественный R говорит о существовании слабой связи между показателями. Причем х₂ является более значимым для данной зависимости у от х₁ и х₂. На тесноту связей могут также оказывать другие факторы, которые не внесены в таблицу наблюдений. Поэтому требуется провести дополнительные наблюдения и проанализировать модель.