Моделирование и идентификация множественной линейной регрессии

3.1. План работы

-в процессе выполнения данной работы необходимо

-синтезировать модель Монте-Карло множественной линейной регрессии (прямая задача).

-вычислить параметры множественной линейной регрессии (обратная задача идентификации).

-составить отчет по работе.

3.2. Модель Монте-Карло множественной линейной регрессии (прямая задача)

Уравнение множественной линейной регрессии.

Множественная линейная регрессия имеет вид

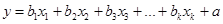, где                             (3.1)

x₁,x₂,x₃, …, x_k, - независимые переменные,

y - зависимая переменная,

a,b₁, b₂, b₃,…, b_k - параметры модели.

В реальности на данную связь оказывает влияние множество других неконтролируемых факторов, в связи с чем данная связь представляется как:

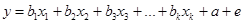, где                         (3.2)

e - случайное отклонение наблюдаемой зависимой переменной, вызванное влиянием других факторов. Уравнение (3.1) является основой статистического моделирования уравнения регрессии.

В рамках данной работы будет моделироваться и идентифицироваться модель третьего порядка:

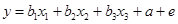
3.2.1. Последовательность выполнения работы по моделированию.

Откроем новую книгу. Cохраним книгу в своей папке под именем МЛР. Xls (Множественная Линейная Регрессия).

Для данной задачи рекомендуется отменить режим автоматического пересчета листа. Для этого необходимо в «Сервис»\ «Параметры»\ «Вычисления» установить режим «вручную».

3.2.1.2. Сформируем заголовки для исходных данных модели (Рисунок 1.1):

- коэффициенты модели,a,b₁, b₂, b₃,…, b_k;

- среднее квадратическое отклонение погрешности СКО_е;

- математическое ожидание независимых переменных М_х1, М_х2, М_х3,;

- среднее квадратическое отклонение независимых переменных СКО_х1,СКО_х2,СКО_х3,

Ввести значения а, b₁, b₂, b₃, CKO_e (σ_е), М_х1, М_х2, М_х3, СКО_х1, СКО_х2, СКО_х3, согласно варианту контрольной работы.

3.2.1.3. СКО_е задать равным нулю.

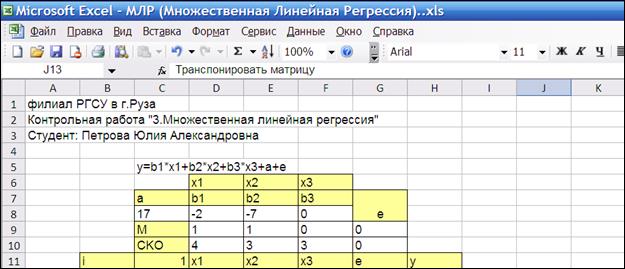
Рисунок 3.1

3.2.1.4. Сформируем заголовки таблицы модели (Рисунок 3.1).

Выделим ячейки для:

i – номер наблюдения,

1 – единичный вектор (будет рассмотрен ниже),

х₁, х₂, х₃ - значения переменных x₁, x₂, x₃,

е – значение ошибки в текущем наблюдении e,

y – моделируемое факторное значения зависимой переменной y, определяемое независимыми переменными x ₁, x ₂, x ₃ и ошибкой e.

3.2.1.5. Моделирование двадцати наблюдения (Рисунок 3.2 (показаны первые 4 наблюдения))

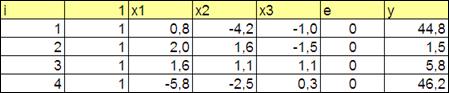
Рисунок 3.2

Колонка единичного вектора заполняется единицами.

Случайные значения независимых переменных x ₁, x ₂, x ₃ – моделируются аналогично предыдущему по формуле

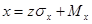, где                                              (3.3)

Z - центрированная и нормированная случайная величина, распределенная по нормальному закону (MZ =0, σZ =1),

M_x, σ_x - математическое ожидание и среднее квадратическое отклонение независимой переменной.

Центрированная и нормированная случайная величина моделируется на основании центральной предельной теоремы путем 12-ти кратного сложения равномерно распределенных случайных чисел R_i в диапазоне (0,1].

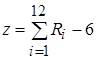                                                   (3.4)

Синтаксис функцией, возвращаемой случайное число, равномерно распределенное в диапазоне (0,1], имеет вид:

R= слчис().

Для моделирования независимой переменной необходимо в ячейку, где моделируется переменная x необходимо ввести формулу:

«=(слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()-6)*[ σx ]+ [ Mx ]», где

[ Mx ] и [ σx ] - соответственно адреса ячеек, где заданы математическое ожидание и среднее квадратическое отклонение независимой переменной (ссылки на данные ячейки должны быть абсолютными).

Аналогично моделируется ошибка в текущем наблюдении e,

Факторное значения зависимой переменной y, определяемое независимыми переменными x ₁, x ₂, x ₃ и ошибкой e вычисляется по формуле (3.2).

3.2.1.6. Задав СКО_е =0 (М_е =0) построим точечные графики зависимости у(х₁), у(х₂), у(х₃) (Рисунок 3.3).

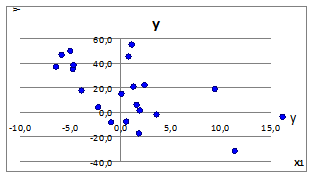
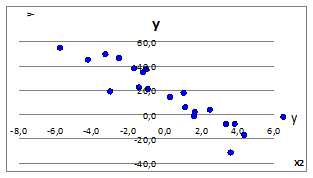
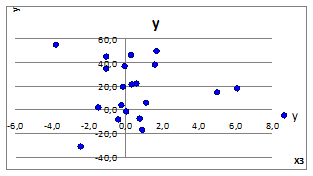
Рисунок 3.3

3.2.1.7. При СКО_е =0 имеем отсутствие линейной связи y (x). Это объясняется тем, что внутри рассматриваемых случаев случайная природа образования зависимости имеет место существовать.

3.3. Идентификация модели множественной линейной регрессии

3.3.1. Основные положения процедуры идентификации параметров множественной линейной регрессии

Задачей идентификации и является нахождение таких значений a, b₁, b₂, b₃, при которых сумма квадратов ошибки будет минимальна

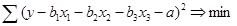                       (3.5)

На основании смоделированных значений наблюдений мы имеем следующую систему уравнений:

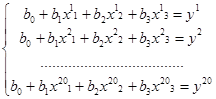                                    (3.6)

Где верхний индекс обозначает номер моделируемого наблюдения.

Если ввести следующие векторы и матрицу как:

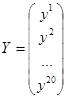
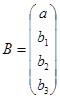
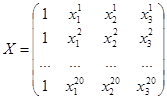,                    (3.7)

то система уравнений может быть записана в векторной форме:

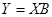                                                  (3.8)

Условие минимума квадрата ошибки в векторной форме будет иметь вид:

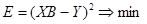                                         (3.9)

Данный минимум обеспечивается при условии равенства нулю производной:

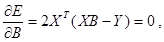  где                                (3.10)

 

Х^Т - транспонированная матрица Х.

Раскрывая скобки получаем:

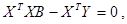                                   (3.11)

Откуда вектор параметров модели будет определяться как:

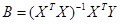                                     (3.12)

3.3.2. Последовательность выполнения работы:

Для расчета элементов вектора В (состоящего из значений коэффициентов регрессионной модели) необходимо последовательно получим:

- транспонированную матрицу - Х^Т,

- произведение - ХХ^Т,

- обратную матрицу – (ХХ^Т)^-1,

- произведение - (ХХ^Т)^-1 Х^Т,

- произведение - (ХХ^Т)^-1 Х^ТY,

3.3.2.1. Получим транспонированную матрицу Х^Т.

Транспонированная матрица получается путем замены срок на столбцы,

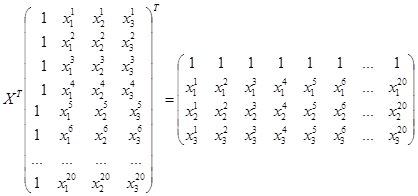
Для получения транспонированной матрицы необходимо:

-выделим исходную матрицу

-кликнем по кнопке «Копирование»,

-кликнем на ячейку, в которой необходимо разместить транспонированную матрицу (20 столбов вправо и 5 строк вниз от нее ячейки должны быть свободными),

-выполним команду «Правка>Специальная вставкa».Поставим флажок «Транспонирование» и нажмем на клавишу ОК.

На рабочем поле появилась транспонированная матрица (Рисунок 3.4 - приводим лишь первые столбцы).

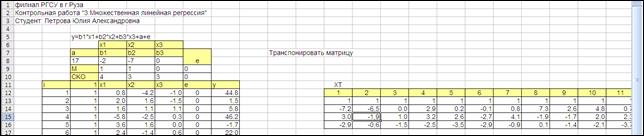
Рисунок 3.4

Убедимся, что процедура транспонирования произведена правильно.

3.3.2.2. Получим произведение матриц ХХ^Т.

Произведение матрицы Х размерностью (20х4) на матрицу Х^Т размерностью (4х20) будет матрица размерностью (4х4).

В этой связи выделим область ячеек 4х4 и введем в них формулу массива умножения матриц «Мунож» (категория «математические»).

В раскрывшемся диалоговом окне (Рисунок 3.5) введем адреса умножаемых массивов.

После чего кликнем по кнопке «ОК», нажмем на клавишу F2 или активизируем строку формул и удерживая клавиши <Shift> и <Ctrl> нажмем на клавишу<Enter>.

В выделенных ячейках появится результат умножения (Рисунок 3.6).

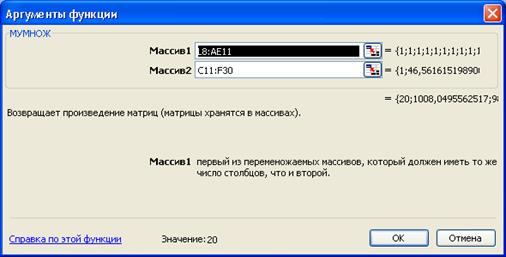
Рисунок 3.5

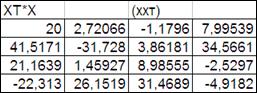
Рисунок 3.6.

3.3.2.3. Получим обратную матрицу (ХХ^Т)^-1.

Выделим ячейки (4х4) для обратной матрицы и ввести в них формулу массива вычисления обратной матрицы «Мобр» (в той же категории). В диалоговом окне ввести адреса исходной обращаемой матрицы и аналогично получить значения ее элементов (Рисунок 3.7)

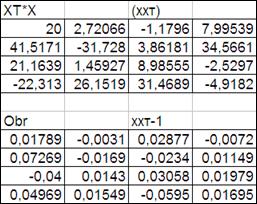
Рисунок 3.7

3.3.2.4. Получим произведение матриц (ХХ^Т)^-1Х^Т.

Произведение матрицы (ХХ^Т)^-1Х^Т размерностью (4х4) на матрицу размерностью (4х20) будет матрица размерностью (4х20).

Следовательно, для ввода формулы массива необходимо выделить ячейки для матрицы размером (4х20). После чего аналогично получить результат умножения (Рисунок 3.8 – приведены первые столбцы результата умножения).

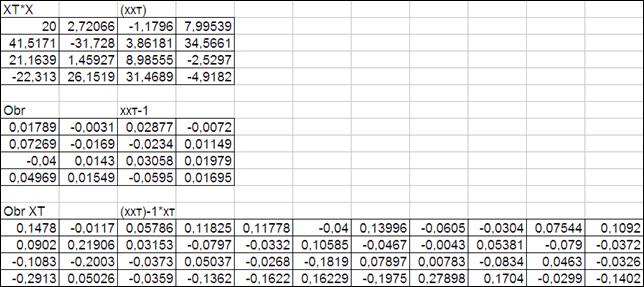
Рисунок 3.8

3.3.2.5. Получим произведение матриц (ХХ^Т)^-1Х^ТY, т.е. вектор коэффициентов В.

Произведение матрицы (ХХ^Т)^-1Х^ТY размерностью (4х20) вектор Y размерностью (20х1) будет вектор размерностью (4х1).

Следовательно, необходимо выделить 4 ячейки на поле и ввести в них аналогично формулу умножения матриц.

Озаглавим слева данные ячейки (a, b₁, b₂, b₃) (Рисунок 3.9)

Значения в этих ячейках должны совпадать с заданными значениями a, b₁, b₂, b₃

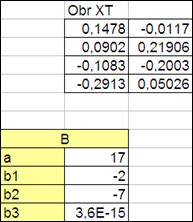
Рисунок 3.9

3.4. Идентификация с помощью «Пакета анализа - Регрессия» ППП Excel

Идентификация с помощью «Пакета анализа - Регрессия» ППП Excel аналогична процедуре идентификации линейной парной регерессии. Отличие заключается в задании входного интервала Х. Для идентификации множественной регрессии необходимо задавать адреса ячеек не одного столбца, а нескольких столбцов (для нашего примера 3), в которых размещены значения независимых переменных x₁, x₂, x₃ (Рисунок 3.10).

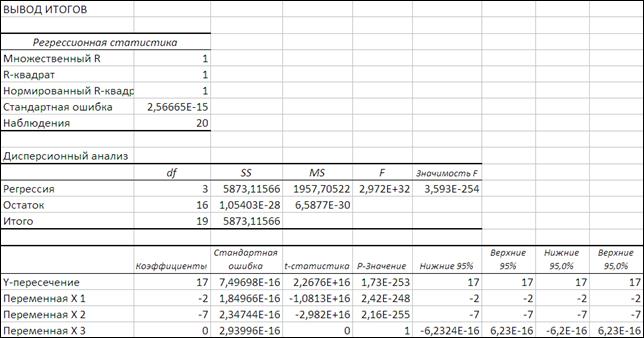
Рисунок 3.10

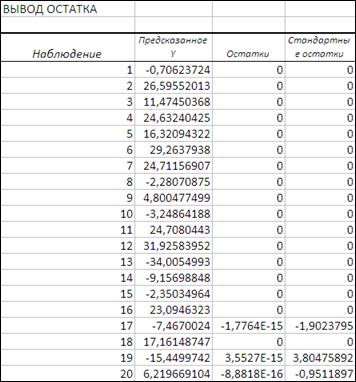
Рисунок 3.11

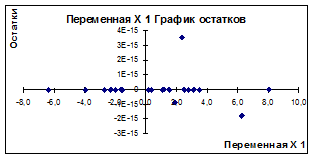
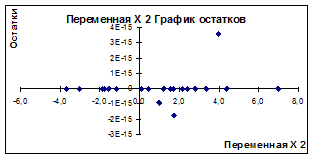
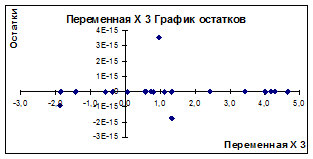
Рисунок 3.12

Уравнение регрессии имеет вид: y =17-2 x₁ -7 x₂

Значимость критерия F показывает, что полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается значимость всего уравнения и показателя тесноты связи (индекса множественной детерминации) R -квадрат оценивает долю вариаций результата за счет представленных в уравнении факторов в общей вариации результата. 100% указывает на полную связь между результативными и факторными признаками. Стандартная ошибка определяет тесноту связи с учетом степени свободы общей и остаточной дисперсии. Она дает тесноту связи, которая не зависит от числа факторов.

3.5. Пример анализа экономических показателей на предприятии.

Исследуем зависимость денежной выручки за несколько месяцев (y) от поступления денежных средств за пребывание льготных категорий граждан (x₁) и среднего возраста льготных категорий.

Дана таблица наблюдений.

Анализ зависимости выручки (y тыс.руб.) санатория "Огонёк" от средней суммы поступлений денежных средств от льготных путевок (x₁ тыс. руб.) и среднего возраста льготной категории (x₂ лет).

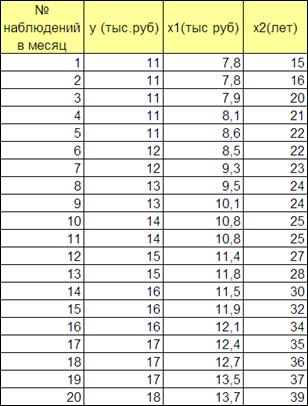
Рисунок 3.13

 

Проведем анализ с помощью «Пакета анализа - Регрессия» ППП Excel.

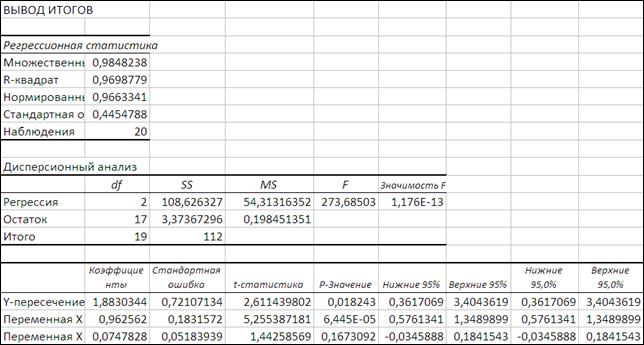
Рисунок 3.14

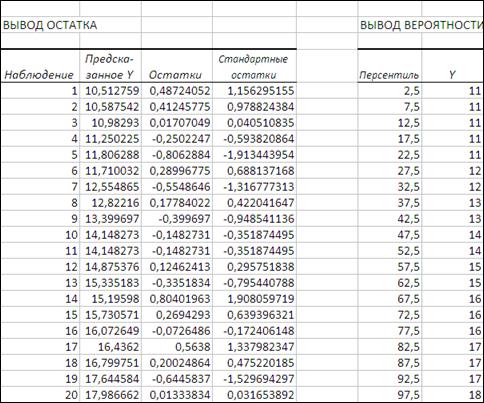
Рисунок 3.15

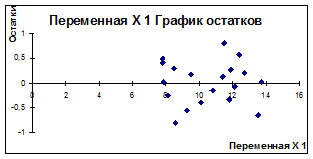
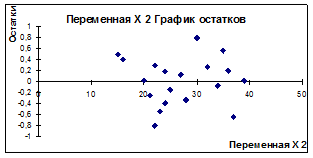
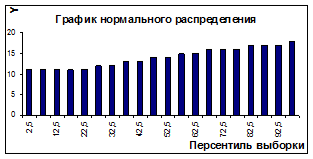
Рисунок 3.16

Уравнение регрессии имеет вид y=1,883+0.9626 x₁ +0.0748 x₂

По множественному R = 0,9699 видим, что связь коэффициентов регрессии тесная. Критерий F_частнх₂ = 2 показывает статическую зависимость включения второго фактора после первого. Прирост факторной дисперсии за счет дополнительного признака х₂ незначительный. Вероятность х₂ случайного формирования много ниже уровня значимости. Прирост факторной дисперсии за счет признак х₁ существенный. Поэтому фактор х₂ можно исключить из рассмотрения и ограничиться парной регрессией y =1,883+0,9626 х₁. Уравнение более простое для анализа и прогноза.