Показникова функція  (рис.5.3).
(рис.5.3).
Функція означена в інтервалі 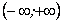 і неперервна в кожній точці цього інтервалу. При
і неперервна в кожній точці цього інтервалу. При  функція зростає; при
функція зростає; при  - спадає. Областю зміни показникової функції є інтервал
- спадає. Областю зміни показникової функції є інтервал 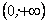 .
.
Логарифмічна функція  (рис.5.4).
(рис.5.4).
Функція означена в інтервалі 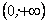 і неперервна в кожній точці цього інтервалу. При
і неперервна в кожній точці цього інтервалу. При  функція зростає; при
функція зростає; при  - спадає.
- спадає.
Область зміни логарифмічної функції складає множина всіх дійсних чисел.
Степенева функція  (рис.5.5, 5.6).
(рис.5.5, 5.6).
Якщо відносно  відомо лише, що це деяке дійсне число, то можна говорити про значення
відомо лише, що це деяке дійсне число, то можна говорити про значення  тільки для
тільки для  . Тому в загальному випадку областю означення степеневої функції вважають інтервал
. Тому в загальному випадку областю означення степеневої функції вважають інтервал 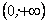 . Якщо
. Якщо  то
то  означена і в точці
означена і в точці  , де приймає значення
, де приймає значення  . При зростанні
. При зростанні  степенева функція
степенева функція  зростає, якщо
зростає, якщо  і спадає, якщо
і спадає, якщо  . Значення у степеневої функції заповнюють інтервал
. Значення у степеневої функції заповнюють інтервал 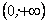 . Якщо число
. Якщо число  - ціле або дробове з непарним знаменником, то степенева функція
- ціле або дробове з непарним знаменником, то степенева функція  при
при  означена для всіх
означена для всіх  , а при
, а при  - для всіх
- для всіх  , крім
, крім  .
.
Тригонометричні функції (рис.5.7, 5.8, 5.9, 5.10).
Функції  і
і  мають областю визначення всі
мають областю визначення всі
значення змінної  . Множиною значень кожної з цих функцій є
. Множиною значень кожної з цих функцій є
відрізок  .
.
Функція  означена для всіх значень
означена для всіх значень  , крім
, крім 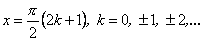 . Множина значень:
. Множина значень:  .
.
Функція  означена для всіх значень
означена для всіх значень  , крім
, крім  . Множина значень:
. Множина значень:  .
.
Обернені тригонометричні функції (рис.5.11, 5.12, 5.13, 5.14).
 - нескінченнозначна функція, обернена для функції
- нескінченнозначна функція, обернена для функції  . Область означення:
. Область означення:  ; область зміни
; область зміни  . Якщо кожному значенню
. Якщо кожному значенню 
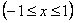 покласти у відповідність значення
покласти у відповідність значення  нескінченнозначної функції
нескінченнозначної функції  , що задовольняє умовам
, що задовольняє умовам  , одержимо однозначну функцію, яку будемо позначати
, одержимо однозначну функцію, яку будемо позначати  і називати головним значенням функції
і називати головним значенням функції  .
.
Функція  - нескінченнозначна, обернена для функції
- нескінченнозначна, обернена для функції  . Область означення:
. Область означення:  ; область зміни:
; область зміни:  . Якщо кожному значенню
. Якщо кожному значенню  ,
,  покласти у відповідність значення
покласти у відповідність значення  нескінченнозначної функції
нескінченнозначної функції  , що задовольняє умовам
, що задовольняє умовам  , одержимо однозначно функцію, яку будемо позначати
, одержимо однозначно функцію, яку будемо позначати  і називати головним значенням функції
і називати головним значенням функції  .
.
Функції  і
і  - нескінченнозначні, обернені відповідно для функцій
- нескінченнозначні, обернені відповідно для функцій  і
і  . Області означення:
. Області означення:  ; області зміни:
; області зміни:  , крім відповідно
, крім відповідно
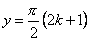 і
і  .
.
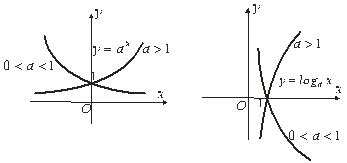
Рис.5.3 Рис.5.4
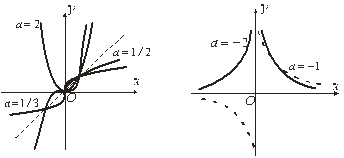
Рис.5.5 Рис.5.6
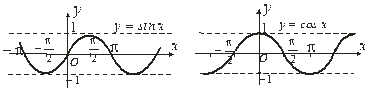
Рис.5.7 Рис.5.8
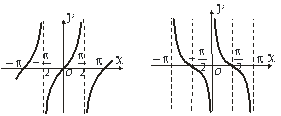
Рис.5.9 Рис.5.10
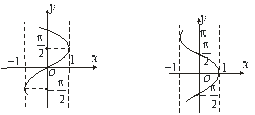
Рис.5.11 Рис.5.12
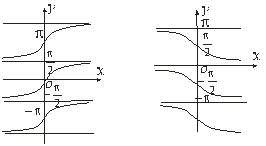
Рис.5.13 Рис.5.14
Якщо кожному значенню  ,
,  , поставити у відповідність значення
, поставити у відповідність значення  функції
функції 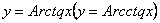 , що задовольняють нерівностям
, що задовольняють нерівностям 
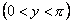 , то одержимо функцію, яку назвемо головним значенням багатозначної функції
, то одержимо функцію, яку назвемо головним значенням багатозначної функції 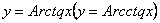 і будемо позначати
і будемо позначати 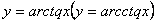 .
.
 2020-01-14
2020-01-14 124
124








