2020-01-14
158
Нехай функцію 
задано на деякому проміжку 
Монотонні функції. Якщо для кожної пари точок 
при 
виконується нерівності:
1) 
то функція 
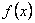називається зростаючою на проміжку 
2) 
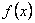то функція називається неспадною на проміжку 
3) 
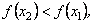то функція 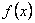називається спадною на проміжку
4) 
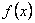то функція називається не зростаючою на проміжку 
Зростаючі, неспадні, спадні та незростаючі функції називаються монотонними.
Приклад.
1. 
Якщо 
то 
тому функція 
є зростаючою в інтервалі 
2. 
. Якщо 
то 
Тому функція 
є спадна в інтервалі 
.
Парні та непарні функції. Нехай функція 
задана на проміжку 
, який є симетричним відносно початку координат. Це може бути: 
Функція на проміжку називається:
1) парною, якщо 
справджується рівність 
2) непарною, якщо справджується рівність 
Зауваження. Графік парної функції симетричний відносно осі ординат, а графік непарної функції симетричний відносно початку координат.
Періодичні функції. Функція , 
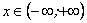
називається періодичною, якщо існує число 
, таке, що 
справджується рівність
|
|
|
.
Число 
при цьому називається періодом функції 
.
Поняття неявної, складної та оберненої функції
Неявна функція
Функція від аргументу 
називається неявною, якщо вона задана рівнянням
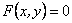(5.1)
Можливі випадки:
1) рівняння (5.1) не задовольняється жодною парою чисел
, тому вона не задає ніякої функції;
2) рівняння (5.1) задовольняється лише однією парою чисел
( 
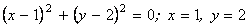), тому воно не задає ніякої залежності;
3) рівняння (5.1) задовольняється різними парами чисел
, тому воно задає змінну як функцію від : .
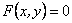Множина значень , для кожного з яких , є областю визначення неявної функції . Наприклад, 
рівняння 
задає двозначну функцію :
; 
.
Нехай тепер маємо рівняння
, (5.2)
що зв’язує значення трьох змінних. Розглянемо множину тих пар чисел 
, для яких існує значення 
, що разом з і рівняння (5.2) перетворює на тотожність.
Якщо кожній парі чисел із вказаної множини поставити у відповідність значення , одержимо однозначну або багатозначну функцію двох змінних: 
, яку будемо називати неявно заданою рівнянням (5.2) або неявною функцією.
Розглянемо рівняння 
, яке зв’язує значення змінних, за аналогією із викладеним, можна ввести
поняття неявної функції від 
змінної.
5.3.2. Складна функція
Розглянемо спочатку функції однієї змінної.
Нехай задані дві функції 
і 
, при цьому множина значень першої функції входить в область означення другої. Тоді кожному значенню із області визначення функції відповідає певне значення змінної , а значенню функція ставить у відповідність певне значення змінної , тобто змінна є функцією : 
.
|
|
|
Одержана функція від функції називається складною функцією змінної . Функція 
- внутрішня, а функція - зовнішня. Наприклад: 
Розглянемо функції багатьох змінних. Тут ми маємо два напрямки.
1. Нехай 
- функція багатьох змінних 
, кожна з яких є функцією незалежної змінної 
: 
. Тоді функція
складна функція незалежної змінної .
Наприклад:
є складна функція незалежної змінної .
2. Нехай - функція багатьох змінних , аргументи якої, в свою чергу, залежать від двох або більшого числа змінних:
.
Тоді функція
буде складною функцією незалежних змінних 
.
Наприклад: 
.
5.3.3. Поняття оберненої функції
Нехай функція визначена в деякій області 
. Візьмемо будь-яке значення
Нехай функція визначена в деякій області . Візьмемо будь-яке значення 
із множини значень цієї функції 
. В області означення функції знайдеться одне або декілька значень аргументу 
таких, що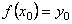 
. Поставимо у відповідність всі ці значення . При цьому кожному значенню змінної 
ставиться у відповідність одне або декілька значень 
. А це означає, що на множині 
задається однозначна або багатозначна функція 
. Вона називається оберненою до функції . Областю. визначення оберненої функції є область зміни даної функції.
Приклади.
1. 
Функція 
є однозначною оберненою функцією для функції 
(рис.5.15).
: 
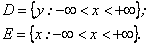
2. 
: 
таких, що . Тому функція 
: 
обернена для функції , буде двозначною (рис.5.16).
Рис.5.15 Рис.5.16
Розглянемо питання про графік оберненої функції. Функція та її обернена функція виражають один і той самий зв’язок між змінними і , лише у першому випадку розглядаємо як аргумент, - як функцію, а в другому випадку – навпаки. Тому графік оберненої функції співпадає з графіком функції (рис.5.17).
Якщо в оберненої функції, як і в заданій, аргумент позначити через , а значення функції - через , то вона запишеться так: .
Рис.5.17 Рис.5.18
Функції , 
різняться лише позначенням змінних. Тому, щоб з графіка функції або, що те саме, функції одержати графік функції , достатньо поміняти ролями всі 
і , тобто повернути площину рисунка навколо бісектриси першого координатного кута на 1800. Звідси графік відносно бісектриси першого координатного кута (рис.5.18).
