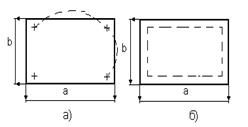
Схематическое изображение конструкции представлено в виде:

где 1 – корпус; 2 – блок функциональных ячеек (нагретая зона);
3 – установочные элементы.
Тепловая модель для нашего конкретного случая имеет вид:

где P - тепловой поток, рассеиваемый конструкцией;
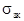 - конвективно-кондуктивная тепловая проводимость между нагретой зоной и внутренней стенкой корпуса;
- конвективно-кондуктивная тепловая проводимость между нагретой зоной и внутренней стенкой корпуса;
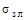 - тепловая проводимость теплопередачи от нагретой зоны к внутренней стенке корпуса излучением;
- тепловая проводимость теплопередачи от нагретой зоны к внутренней стенке корпуса излучением;
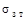 - тепловая проводимость установочных элементов;
- тепловая проводимость установочных элементов;
 - тепловая проводимость стенок кожуха;
- тепловая проводимость стенок кожуха;
 - тепловая проводимость от наружной поверхности корпуса к среде для конвективной теплопередачи,
- тепловая проводимость от наружной поверхности корпуса к среде для конвективной теплопередачи, 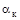 - коэффициент теплопередачи;
- коэффициент теплопередачи;
 - тепловая проводимость от наружной стенки корпуса к среде для теплопередачи излучением;
- тепловая проводимость от наружной стенки корпуса к среде для теплопередачи излучением;
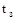 ,
, 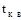 и
и 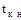 - температуры поверхности нагретой зоны и корпуса;
- температуры поверхности нагретой зоны и корпуса;
 – температура внутренней окружающей среды.
– температура внутренней окружающей среды.
Для определения  - коэффициента конвективной теплопередачи и
- коэффициента конвективной теплопередачи и  - коэффициент теплопередачи излучением воспользуемся номограммами.
- коэффициент теплопередачи излучением воспользуемся номограммами.
А для этого зададим значение температурного перегрева  , температуру окружающей среды
, температуру окружающей среды  .
.
Определим температуру корпуса в первом приближении:
 ;
;
Определим среднюю температуру между корпусом и средой в первом приближении: 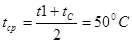 ;
;
Найдем определяющий размер нагретой конструкции: 
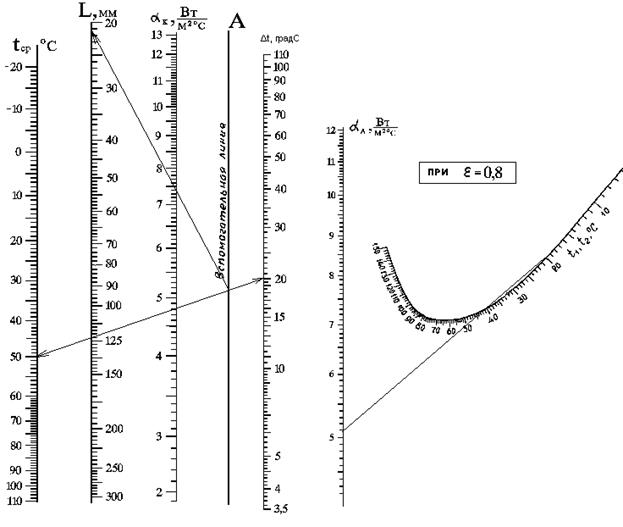
Таким образом 
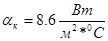 ;
;  при
при  .
.
Пересчёт при 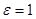 ,
,  .
.
Рассчитаем площади наружной и внутренней поверхности корпуса:
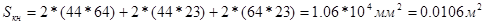

Определим тепловую проводимость от наружной поверхности корпуса к среде для конвективной теплопередачи:

где  - площади наружной поверхности корпуса.
- площади наружной поверхности корпуса.
Определим тепловую проводимость от наружной стенки корпуса к среде для теплопередачи излучением:

где  - площади наружной поверхности корпуса.
- площади наружной поверхности корпуса.
Найдем тепловую проводимость стенок кожуха:

где 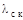 - коэффициент теплопроводности материала корпуса (АБС),
- коэффициент теплопроводности материала корпуса (АБС),  - толщина стенки,
- толщина стенки,  ,
,  - площади внутренней и наружной поверхностей корпуса.
- площади внутренней и наружной поверхностей корпуса.
Определим тепловая проводимость установочных элементов:

где n - число элементов, l - коэффициент теплопроводности материала, l - длина установочных элементов по направлению теплового потока,  - площадь средней изотермической поверхности, перпендикулярной направлению теплового потока.
- площадь средней изотермической поверхности, перпендикулярной направлению теплового потока.
Определим тепловая проводимость теплопередачи от нагретой зоны к внутренней стенке корпуса излучением:

где  - коэффициент теплопередачи излучением;
- коэффициент теплопередачи излучением;  -площадь поверхности нагретой зоны.
-площадь поверхности нагретой зоны.
Найдём конвективно-кондуктивная тепловую проводимость между нагретой зоной и внутренней стенкой корпуса:

где k - поправочный коэффициент на конвективный теплообмен в условиях ограниченного пространства,  - коэффициент теплопроводности воздуха для среднего значения температуры воздуха в прослойке,
- коэффициент теплопроводности воздуха для среднего значения температуры воздуха в прослойке, 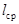 - среднее расстояние между нагретой зоной и кожухом,
- среднее расстояние между нагретой зоной и кожухом,  -площадь поверхности нагретой зоны,
-площадь поверхности нагретой зоны,  - площадь внутренней поверхности корпуса.
- площадь внутренней поверхности корпуса.
Найдем температуру наружной стенки корпуса:
 ;
;
Найдем температуру внутренней стенки корпуса:
 ;
;
Найдем температуру нагретой зоны:
 .
.
На основе полученных данных принимаем решение о естественном воздушном охлаждении устройства, что подтверждает оценочный расчёт системы охлаждения конструкции.
Оценка вибропрочности планарных конструкций.
Конструкция считается вибропрочной, если в ней отсутствуют механические резонансы, а допустимая виброперегрузка на резонансной частоте превышает перегрузку, указанную в техническом задании на изделие.
Отсутствие в конструкциях механических резонансов характеризуется следующим соотношением частоты свободных колебаний  любого элемента конструкции и верхней частоты
любого элемента конструкции и верхней частоты  диапазона внешних вибрационных воздействий:
диапазона внешних вибрационных воздействий:  .
.
Для оценки вибропрочности конструкции произведем расчёт частоты свободных колебаний 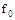 и допустимой величины виброперегрузки.
и допустимой величины виброперегрузки.
Выберем функциональную ячейку на печатной плате, закрепляемую в четырех точках по углам (рис. а), представленную расчетной моделью пластины, равномерно нагруженной радиоэлементами, со свободным опиранием всех сторон (рис. б).
|
|
Определим частоту свободных колебаний основного тона прямоугольной пластины 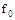 по формуле:
по формуле:
 , где
, где
частотная постоянная 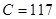 ;
;
толщина пластины 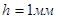 ;
;
большая сторона пластины 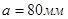 ;
;
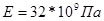 ,
,  - модуль упругости материала пластины и стали;
- модуль упругости материала пластины и стали;
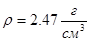 ,
,  - плотность материала пластины и стали;
- плотность материала пластины и стали;
поправочный коэффициент на материал пластины  ;
;
масса пластины 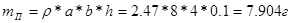 ;
;
выберем массу элементов  из расчёта, что
из расчёта, что  ;
;
поправочный коэффициент на нагружение пластины равномерно размещенными на ней элементами  .
.
Определим допустимую величину вибрационной перегрузки  .
.
 2020-01-14
2020-01-14 137
137