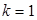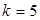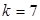Потеря точности в методе Лобачевского–Греффе

 

 

Коэффициенты многочлена в методе Лобачевского–Греффе растут неодинаково быстро и вскоре становятся величинами разного порядка.

Число преобразований многочлена обычно бывает невелико, и точность коэффициентов последнего многочлена по сравнению с точностью коэффициентов первого многочлена уменьшается за счет ошибок округления не более чем на две-три значащие цифры.

Разность между корнем последнего многочлена, взятым с обратным знаком, и соответствующей степенью корня исходного многочлена не превосходит, очевидно, безусловной погрешности корня последнего многочлена, обусловленной погрешностью округления.

Относительная безусловная погрешность корня довольно часто бывает величиной примерно такого же порядка, как и погрешность коэффициентов многочлена. Таким образом, относительная погрешность корня последнего многочлена лишь на несколько порядков превосходит погрешность округления.

При извлечении корня степени 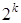 относительная погрешность уменьшается в  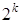раз, так что относительная погрешность найденного по методу Лобачевского–Греффе модуля корня оказывается величиной такого же порядка, что и погрешность округления. Таким образом метод Лобачевского–Греффе для однократных корней дает очень малую потерю точности.

 

 

Другие методы решения алгебраических уравнений с комплексными корнями

 

 

Иногда для нахождения корней уравнения целесообразно использовать другие методы вычислений. В ряде случаев, например при слабой сходимости метода, к найденному с меньшей точностью корню применяются методы уточнения корней. В данном разделе рассмотрены некоторые из существующих методов, которые обладают более простой чем в методе Лобачевского–Греффе вычислительной схемой.

 

 

Метод Бернулли

 

 

Метод Бернулли [2] позволяет найти наибольший и наименьший по модулю корень алгебраического уравнения, но и несколько ближайших к нему (по модулю) корней.

Вычисления по методу Бернулли сводятся в основном к построению некоторой последовательности чисел , для построения которой выбираются вначале некоторые, вообще говоря, произвольные значения . После этого значения  вычисляются с помощью рекуррентной формулы:

 

,

 

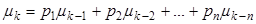Далее по виду последовательности определяется вид наибольшего (наименьшего) по модулю корня и значение этого корня.

Далее после того, как наибольший корень вычислен с достаточной степенью точности, определяется второй по величине модуля корень. Для второго корня строиться новая последовательность , вид которой определяется на основании типа сходимости последовательности построенной для предыдущего корня.

После того как найден второй по модулю корень, аналогично находятся третий и последующие корни.

Пусть погрешность округления во всех вычислениях постоянна и равна . Тогда относительная погрешность первого корня равна [2]

 

, где .

 

Потеря точности для последующих корней может быть значительно больше.

Таким образом, метод Бернулли обладает очень простой вычислительной схемой. Основные вычисления сводятся к повторению операции накопления, что делает метод удобным для вычисления на ЭВМ. Но с другой стороны для реализации метода необходим более сложный, чем для метода Лобачевского–Греффе, логический аппарат, определяющий тип сходимости последовательности . Кроме того, корни в методе Бернулли определяются не все сразу, а один или несколько наибольших (наименьших) по модулю корней, что приводит к потере точности для остальных корней.

 

 

Метод Лина

 

 

Метод Лина [2] служит для нахождения делителей любой степени для заданного многочлена. Чаще всего этот метод используется для нахождения квадратичных делителей, определяющих пару комплексных сопряженных корней многочлена. Этот метод также можно применить для вычисления наибольшего по модулю корня.

Метод Лина может не привести к нахождению делителя, либо привести к нахождению не того делителя, который предполагалось вычислить.

Рассмотрим многочлен (1.3) и найдем его делитель k-й степени

 

.

 

Для этого возьмем какой-нибудь приведенный многочлен  степени k и разделим  на . Тогда полученный остаток будет иметь, вообще говоря, ту же степень k. Разделив его на коэффициент при старшем члене получим приведенный многочлен . Проделав с многочленом  те же операции, что и с  получим  и т.д. Последовательность многочленов 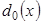, , ,… сходится к  при условии, что для всех k

 

 

где  – корни многочлена .

Вычислительная схема метода Лина достаточно проста, но вычисление корней может потребовать довольно большой вычислительной работы, а иногда может даже не привести к результату. При использовании метода Лина для вычисления комплексных корней целесообразно применять метод ускорения сходимости Хеда [2].

2 ПРАКТИЧЕСКАЯ ЧАСТЬ

 

 

Задание 1

 

Методом Лобачевского–Греффе решить уравнение:

 

.                               (2.1)

 

Сначала установим количество действительных и комплексных корней в уравнении (2.1). Для этого воспользуемся теоремой Штурма.

Система Штурма для уравнения (2.1) будет иметь следующий вид:

 

 

Откуда получаем

 

Таблица 2.1.

Многочлен	Точки на действительной оси
	+	+
	–	+
	–	–
	–	+
	–	–
Число перемен знаков	1	3

Таким образом, получаем, что число действительных корней в уравнении (2.1) равно

 

,

 

т.е. уравнение (2.1) содержит 2 действительных и два комплексных корня.

Для нахождения корней уравнения воспользуемся методом Лобачевского–Греффе для пары комплексно–сопряженных корней.

Произведем квадрирование корней уравнения. Вычисления коэффициентов производились по следующей формуле

 

,                                        (2.2)

 

где

 

,                               (2.3)

 

а 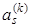 считается равным 0 при .

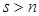Результаты вычислений с восьмью значащими цифрами приведены в таблице 2.2

 

Таблица 2.2.

i	0	1	2	3	4
	0	-3.8000000E+01	3.5400000E+02	3.8760000E+03	0
	1	4.3000000E+01	7.1500000E+02	4.8370000E+03	1.0404000E+04
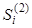
	0	-1.4300000E+03	-3.9517400E+05	-1.4877720E+07	0
	1	4.1900000E+02	1.1605100E+05	8.5188490E+06	1.0824322E+08
	0	-2.3210200E+05	-6.9223090E+09	-2.5123467E+13	0
	1	-5.6541000E+04	6.5455256E+09	4.7447321E+13	1.1716594E+16
	0	-1.3091051E+10	5.3888712E+18	-1.5338253E+26	0
	1	-9.8941665E+09	4.8232776E+19	2.0978658E+27	1.3727857E+32
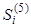
	0	-9.6465552E+19	4.1513541E+37	-1.3242653E+52	0
	1	1.4289776E+18	2.3679142E+39	4.3877982E+54	1.8845406E+64
	0	-4.7358285E+39	-1.2540130E+73	-8.9248610+103	0
	1	-4.7337865E+39	5.6070053E+78	1.9252683+109	3.5514932+128
	0	-1.1214011E+79	1.8227619+149	-3.9826483+207	0
	1	1.1194724E+79	3.1438509+157	3.7066582+218	1.2613104+257

 

 

Как видно из таблицы 2.2 на 7-м шаге корни ,  (считая в порядке убывания модулей) можно считать отделенными. Модули корней находим по формуле (1.27) и грубой прикидкой определяем их знак:

 

 

Так как преобразованный коэффициент при  меняет знак, то данное уравнение имеет комплексные корни, которые определяются из уравнения (1.31) с использованием формул (1.29) и (1.30):

 

i.

 

Относительная погрешность корней, вычисленная по формуле (1.28) равна

 

,

,

.

 

 

Задание 2

 

Методом Лобачевского–Греффе решить уравнение:

 

.                           (2.4)

 

Для начала с помощью теоремы Штурма определим количество действительных и комплексных корней в уравнении (2.2).

Для данного уравнения система Штурма имеет вид

 

Откуда получаем

 

Таблица 2.3.

Многочлен	Точки на действительной оси
	+	+
	–	+
	+	+
	–	+
	–	–
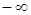
Число перемен знаков	3	1

 

Таким образом, получаем, что число действительных корней в уравнении (2.2) равно

 

,

 

т.е. уравнение (2.2) содержит 2 действительных и два комплексных корня.

Для приближенного нахождения корней уравнения воспользуемся методом Лобачевского–Греффе для пары комплексно–сопряженных корней.

Произведем квадрирование корней уравнения. Вычисления коэффициентов произведем по формулам (2.2) и (2.3).

Результаты вычислений с восьмью значащими цифрами приведены в таблице 2.4

 

Таблица 2.4.

i	0	1	2	3	4
	0	-9.2000000E+00	-3.3300000E+01	1.3800000E+02	0
	1	1.6900000E+00	-1.2140000E+01	1.3825000E+02	2.2500000E+02
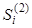
	0	2.4280000E+01	-1.7285000E+01	5.4630000E+03	0
	1	2.7136100E+01	1.3009460E+02	2.4576062E+04	5.0625000E+04
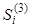
	0	-2.6018920E+02	-1.2325470E+06	-1.3172078E+07	0
	1	4.7617872E+02	-1.2156224E+06	5.9081077E+08	2.5628906E+09
	0	2.4312447E+06	-5.5753725E+11	6.2310144E+15	0
	1	2.6579909E+06	9.2020050E+11	3.5528838E+17	6.5684084E+18
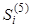
	0	-1.8404010E+12	-1.8886934E+24	-1.2088505E+31	0
	1	5.2245148E+12	-1.0419245E+24	1.2621774E+35	4.3143988E+37
	0	2.0838490E+24	-1.3188529E+48	8.9905555E+61	0
	1	2.9379403E+25	-2.3324632E+47	1.5930919E+70	1.8614037E+75
	0	4.6649263E+47	-9.3608180E+95	8.6833113+122	0
	1	8.6361583E+50	-8.8167795E+95	2.5379418+140	3.4648238+150

 

Как видно из таблицы 2.4 на 7-м шаге корни ,  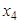(считая в порядке убывания модулей) можно считать отделенными. Модули корней находим по формуле (1.27) и грубой прикидкой определяем их знак:

 

 

Так как преобразованный коэффициент при  меняет знак, то данное уравнение имеет комплексные корни, которые определяются из уравнения (1.31) с использованием формул (1.29) и (1.30):

 

i.

 

Относительная погрешность корней, вычисленная по формуле (1.28) равна

 

,

.