2020-01-14
144
Пусть 
– неопределенный параметр, малый настолько, что его первой степенью еще нельзя пренебрегать в вычислениях, а второй и более высокими степенями можно пренебрегать.
Для простоты предположим, что
(1.32)
Разложим многочлен (1.3) по степеням 
:
.
Проделаем преобразования Лобачевского–Греффе над многочленом 
. Как легко доказать [2], коэффициенты многочлена, полученного после k-го преобразования, будут иметь следующий вид
.
Пусть 
– корень однократного модуля. Тогда при достаточно малом 
представляет собой корень однократного модуля многочлена 
. Его можно найти по формуле
При выполнении операций деления и извлечения корней над числами вида 
можно пользоваться следующими формулами:
,
.
Тогда
, (1.33)
где
.
Так как 
, то приравнивая модули коэффициентов при 
, получим:
.
Заменяя 
через 
, будем иметь 
.
Перепишем теперь равенство (1.33) в виде 
.
Из соотношения 
следует, что при положительном 
и положительном 
. Из соотношения (1.33) видно тогда, что 
должно быть отрицательным. Аналогично получаем, что при отрицательном и положительном 
должно быть 
, так что
.
Эта формула дает возможность вычислить корни однократного модуля без извлечения корней степени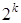 
и без неопределенности в знаке.
Рассмотрим теперь, как вычислить корни двукратного модуля 
, 
(по ранее сделанному предположению эти корни являются комплексно сопряженными). Для этого найдем квадратичный делитель 
, где
