Метод Лобачевского-Греффе для случая комплексных корней

Рассмотрим теперь случай когда среди корней уравнения (1.3) содержаться одинаковые по модулю, тогда из предположения, что уравнение (1.3) не содержит кратных корней, следует, что если , то  и – коплексно-сопряженные.

Характерным признаком этого является тот факт, что при квадрировании корней коэффициент при  в уравнении (1.25), меняет знак, так как при наличии лишь действительных корней все коэффициенты преобразованных уравнений неотрицательны.

Согласно общей теории отделенных корней [1] корни  и , соответствующие комплексным корням  и , приближенно удовлетворяют квадратному уравнению

.

Откуда получаем модули корней по формуле

                              (1.27)

Относительную погрешность модуля найденного по формуле (1.27), без учета погрешности округлений при преобразованиях многочлена, можно оценить следующей величиной [2]

,              (1.28)

где

Комплексные корни можно найти воспользовавшись первым и последним равенством из системы (1.7). Откуда

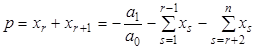,                    (1.29)

.                               (1.30)

Тогда  и  находятся из квадратного уравнения

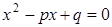.                                           (1.31)