СЛУЧАЙНЫЕ ПРОЦЕССЫ
Оглавление
Случайная функция, случайный процесс, случайное поле. 2
Функция распределения вероятностей случайного процесса. 3
Плотность распределения вероятностей случайного процесса. 4
Моментные функции случайного процесса. 5
Условные распределения вероятностей. 6
Примеры математических моделей случайных процессов. 7
Стационарные процессы.. 8
Литература. 10
Случайная функция, случайный процесс, случайное поле
69.1. Случайной функцией  называется случайная величина
называется случайная величина  , зависимая от параметра
, зависимая от параметра  . Случайные величины
. Случайные величины  могут быть вещественными, либо комплексными, либо векторными; аргумент
могут быть вещественными, либо комплексными, либо векторными; аргумент  может быть вещественным или векторным. Самый простой пример случайной функции получаем для вещественного параметра
может быть вещественным или векторным. Самый простой пример случайной функции получаем для вещественного параметра  и вещественной случайной величины
и вещественной случайной величины  . При этом
. При этом  называется случайной функцией одной переменной или случайным процессом. Отметим, что аргумент
называется случайной функцией одной переменной или случайным процессом. Отметим, что аргумент  случайного процесса не обязательно имеет размерность времени.
случайного процесса не обязательно имеет размерность времени.
Более сложные примеры случайных функций встречаются в задачах физики, океанологии, метеорологии и других областях приложения теории вероятностей. Так, температура воздуха  в точке пространства
в точке пространства  и в момент времени
и в момент времени  часто рассматривается как случайная величина. Таким образом, температура воздуха
часто рассматривается как случайная величина. Таким образом, температура воздуха  является случайной функцией, зависимой от трех декартовых координат
является случайной функцией, зависимой от трех декартовых координат  времени
времени  . Случайную функцию, зависимую от нескольких переменных принято называть случайным полем.
. Случайную функцию, зависимую от нескольких переменных принято называть случайным полем.
69.2. Случайный процесс  как функция аргумента
как функция аргумента  имеет свою область определения
имеет свою область определения 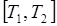 , которая может быть отрезком на вещественной оси, положительной полуосью, всей вещественной осью и т. д. Рассмотрим случайный процесс
, которая может быть отрезком на вещественной оси, положительной полуосью, всей вещественной осью и т. д. Рассмотрим случайный процесс  при фиксированном
при фиксированном  , тогда
, тогда  - случайная величина, которая называется сечением случайного процесса в точке
- случайная величина, которая называется сечением случайного процесса в точке  .
.
Пусть выполняется  опытов, в каждом из которых измеряется значение
опытов, в каждом из которых измеряется значение  ,
,  , случайной величины
, случайной величины  . Тогда результаты измерений – это
. Тогда результаты измерений – это  чисел
чисел
 . (69.1)
. (69.1)
В отличие от случайной величины  измерение случайного процесса
измерение случайного процесса  выполняется в течение некоторого интервала
выполняется в течение некоторого интервала  -интервала наблюдения. Последний либо содержится в области определения
-интервала наблюдения. Последний либо содержится в области определения 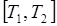 , либо совпадает с ней. Пусть детерминированная функция
, либо совпадает с ней. Пусть детерминированная функция  ,
,  , - результат измерения случайного процесса в первом опыте, функция
, - результат измерения случайного процесса в первом опыте, функция  ,
,  , - результат измерения случайного процесса во втором опыте, и т.д. Тогда результаты всех
, - результат измерения случайного процесса во втором опыте, и т.д. Тогда результаты всех  опытов, аналогично (69.1), представляются совокупностью
опытов, аналогично (69.1), представляются совокупностью  детерминированных функций времени:
детерминированных функций времени:
 (69.2)
(69.2)
Каждая функция 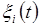 ,
,  , называется реализацией (траекторией, выборочной функцией, выборкой) случайного процесса
, называется реализацией (траекторией, выборочной функцией, выборкой) случайного процесса  . Совокупность (69.2) называется ансамблем реализаций случайного процесса
. Совокупность (69.2) называется ансамблем реализаций случайного процесса  . Ансамбль реализаций содержит информацию о статистических свойствах случайного процесса
. Ансамбль реализаций содержит информацию о статистических свойствах случайного процесса  аналогично как и совокупность измерений (69.1) содержит информацию о статистических свойствах случайной величины
аналогично как и совокупность измерений (69.1) содержит информацию о статистических свойствах случайной величины  .
.
69.3. В зависимости от того, дискретны или непрерывны время  и реализации
и реализации 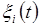 , различают четыре типа случайных процессов.
, различают четыре типа случайных процессов.
1). Случайный процесс общего типа: время  - непрерывно и реализации
- непрерывно и реализации 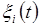 - непрерывны.
- непрерывны.
2). Дискретный случайный процесс: время  - непрерывно и
- непрерывно и 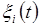 - дискретны.
- дискретны.
3). Случайная последовательность:  - дискретно и
- дискретно и 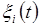 - непрерывны. В литературе случайные процессы этого типа принято называть временными рядами.
- непрерывны. В литературе случайные процессы этого типа принято называть временными рядами.
4). Дискретная случайная последовательность:  - дискретно и
- дискретно и 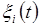 - дискретны.
- дискретны.
 2020-01-14
2020-01-14 240
240







