2020-01-14
212
70.1. При фиксированном 
распределение вероятностей сечения 
случайного процесса (как распределение вероятностей случайной величины) задается функцией распределения вероятностей
. (70.1)
Соотношение (70.1) можно рассматривать при любом 
. Функция 
, как функция двух переменных 
и , называется одномерной функцией распределения вероятностей случайного процесса . Аргументы и принято называть соответственно фазовой и временной переменными. Однако, не дает исчерпывающую вероятностную характеристику случайного процесса , поскольку она не учитывает зависимости случайных величин при разных (т.е. зависимости разных сечений случайного процесса). Более полно вероятностные свойства случайного процесса описывает 
-мерная функция распределения 
- функция распределения случайного вектора 
:
. (70.2)
Однако, практическое применение находят лишь функции распределения первого и второго порядков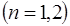 
. Функции более высоких порядков 
используются только в теории.
70.2. Основные свойства -мерной функции распределения вероятностей случайного процесса аналогичны свойствам функции распределения вероятностей -мерного вектора.
1) Функция 
- неубывающая по каждому аргументу 
, 
.
2) Функция 
- непрерывна справа по каждому аргументу 
, 
.
3) Функция распределения симметрична относительно перестановок двух любых пар 
и 
:
.
4) Для любого целого 
, 
.
5) Для любого целого ,
.
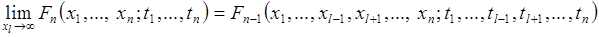6) 
.
