2020-01-14
111
Если задана 
- мерная плотность распределения вероятности случайного процесса 
, тогда условная плотность 
порядка 
при условии, что случайный процесс в моменты времени 
принимает значения 
определяется по формуле:
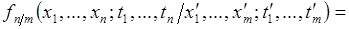
. (73.1)
Соответствующая условная функция распределения вероятностей 
порядка при условии, что случайный процесс в моменты времени 
принимает значения определяется соотношением:
. (73.2)
Соотношения между условной плотностью 
и условной функцией распределения вероятностей 
аналогичны соотношениям для соответствующих безусловных функций, например, справедливо равенство:
. (72.3)
В простейшем варианте при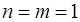 
формула (73.1) для условных плотностей принимает вид:
. (73.4)
Отсюда
. (73.5)
Поскольку плотность второго порядка симметрична относительно перестановок пар 
и 
, то из (73.5) следует
. (73.6)
Соотношения (73.5), (73.6) - это формулы умножения для плотностей. Очевидна аналогия этих формул с формулой умножения вероятностей. Используя свойство согласованности, из (73.6) получим
. (73.7)
Это соотношения аналогично формуле полной вероятности. Далее, выражения (73.6), (73.7) подставим в (73.4), тогда
. (73.8)
Данное соотношение представляет собой аналог формулы Байеса.
