Для центральных механизмов радиус кривошипа:
r=lAB=0,5 So м (1.9)
где So- общий ход иглы, равный сумме перемещения иглы от крайнего верхнего по-
ложения до начала входа иглы в материал и перемещения в материале.
Длина шатуна вычисляется по формуле: l = lBC = r/l м (1.10)
По нашему условию So= 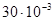 м, а l=0,38; таким образом r=
м, а l=0,38; таким образом r= 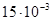 м, а l»0,039
м, а l»0,039
Кинематический анализ кривошипно-ползунного механизма.
Задачи анализа.
Исходными данными для кинематического анализа являются: схема механизма, длина звеньев и закон движения входного звена (кривошипа).
Задачи кинематического анализа:
· Построение плана положений звеньев механизма.
· Определение линейных скоростей и ускорений точек звеньев.
· Определение угловых скоростей и ускорений звеньев.
Построение плана механизма.
Для кинематического исследования строится кинематическая схема механизма, на которой изображается ряд положений всех звеньев механизма (план механизма).
План механизма строится в некотором масштабе. Если кривошип r=lAB на плане механизма изображается отрезком 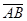 в мм, то длина этого отрезка называется масштабным значением длины кривошипа. Тогда истинное значение длины кривошипа:
в мм, то длина этого отрезка называется масштабным значением длины кривошипа. Тогда истинное значение длины кривошипа:
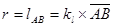 м (1.11)
м (1.11)
где kl – масштаб длин (масштаб плана механизма).
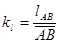 м/мм (1.12)
м/мм (1.12)
Масштаб длин соответствует числу метров истинной длины звеньев в одном миллиметре чертежа и является размерной величиной, в отличие от чертежных масштабов.
В выбранном масштабе вычисляются длины отрезков на чертеже, соответствующих остальным звеньям:
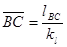 мм (1.13)
мм (1.13)
На основании исходных данных зададим величину отрезка 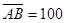 мм, тогда масштаб механизма kl=0,00015 м/мм, а длина отрезка соответствующего шатуну
мм, тогда масштаб механизма kl=0,00015 м/мм, а длина отрезка соответствующего шатуну 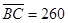 мм.
мм.
Проведем траекторию движения точки В, радиусом 100 мм, и разделим ее на 8 частей. Примем крайнее левое положение кривошипа за нулевое. По ходу движения присвоим номера положениям кривошипа. Для нахождения положений ползуна, соотвотствующих положениям кривошипа, из точек В0, В1, etc., радиусом 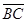 проводим дуги до пересечения с прямой АС. Соединяя соответствующие точки, показываем кривошип и шатун в различных положениях. Для одного из положений (в нашем случае для первого) на звеньях укажем центры масс тяжести S1 (для кривошипа) и S2 (для шатуна).
проводим дуги до пересечения с прямой АС. Соединяя соответствующие точки, показываем кривошип и шатун в различных положениях. Для одного из положений (в нашем случае для первого) на звеньях укажем центры масс тяжести S1 (для кривошипа) и S2 (для шатуна). 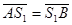 =50 мм;
=50 мм; 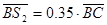 =91 мм.
=91 мм.
Построение плана скоростей.
План скоростей позволяет вычислить линейную скорость любой точки звеньев, угловую скорость звеньев и служит основой для нахождения уравновешивающего
момента по способу профессора Н.Е. Жуковского.
Определим для первого положения линейную скорость точек A, B, C, S1, S2 и угловую скорость шатуна w2. Входным является кривошип АВ, вращающийся с угловой скоростью w1= const, Частота вращения n1=2500 об/мин.
Точка В является общей для звеньев 1 и 2. Звено 1 совершает вращательное движение. Следовательно величина скорости точки В:
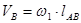 м/с (1.14)
м/с (1.14)
где 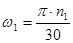 - угловая скорость кривошипа, 1/с;
- угловая скорость кривошипа, 1/с;
lAB – истинная длина кривошипа, м;
n1 – частота вращения кривошипа, об/мин
Исходя из нашего условия VB=3,93 м/с
Вектор скорости 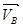 характеризуется точкой приложения (в точке В), линией действия (по касательной к траектории в точке В, либо перпендикулярно кривошипу АВ) и направлением (по часовой стрелке согласно направлению вращения кривошипа).
характеризуется точкой приложения (в точке В), линией действия (по касательной к траектории в точке В, либо перпендикулярно кривошипу АВ) и направлением (по часовой стрелке согласно направлению вращения кривошипа).
Точка С принадлежит звеньям 2 и 3 и движется вдоль прямой АС вместе со звеном 3. Следовательно, линия действия вектора скорости 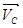 известна, а модуль и направление неизвестны. Точки В и С принадлежат одному звену – шатуну ВС, поэтому между скоростями этих точек есть определенная связь.
известна, а модуль и направление неизвестны. Точки В и С принадлежат одному звену – шатуну ВС, поэтому между скоростями этих точек есть определенная связь.
Шатун ВС в абсолютном движении относительно неподвижного звена – стойки совершает плоское (плоскопараллельное) движение. Которое можно представить в виде сумм двух простых движений: переносного (поступательного) и относительного (вращательного). При поступательном движении точки описывают одинаковые траектории, любая прямая, принадлежащая звену, остается параллельной самой себе, скорости всех точек равны между собой и параллельны, а угловая скорость равна нулю.
 (1.15)
(1.15)
Однако, в абсолютном движении относительно стойки точка С движется вместе с ползуном вдоль прямой АС, поэтому действительной положение точки С определяет- ся относительным вращательным движением шатуна ВС вокруг точки В. Поэтому абсолютная скорость точки С:
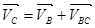 (1.16)
(1.16)
где VBC – относительная скорость точки С при повороте шатуна ВС вокруг точки В.
Примем точку В за полюс, т.к. нам известны все характеристики вектора скорости 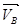 ; у вектора скорости
; у вектора скорости 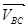 известна только линия действия, расположенная перпендикулярно радиусу вращения ВС; у вектора скорости
известна только линия действия, расположенная перпендикулярно радиусу вращения ВС; у вектора скорости 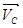 известна тоже только линия действия.
известна тоже только линия действия.
Для определения векторов скорости 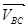 и
и 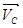 решим векторное уравнение (1.16). План скоростей как раз и представляет собой графическое решение векторных уравнений.
решим векторное уравнение (1.16). План скоростей как раз и представляет собой графическое решение векторных уравнений.
Для построения плана скоростей задается его масштаб:
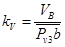
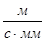 (1.17)
(1.17)
где PV3b – длина отрезка, изображающего на плане скоростей скорость точки В, мм
Пусть PV3b=130 мм, тогда kv=0,03 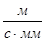
Из полюса на плане скоростей PV3 откладываем отрезок прямой 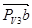 перпендикулярно звену АВ3 в сторону его движения. Затем через точку b линию действия вектора вращательной скорости
перпендикулярно звену АВ3 в сторону его движения. Затем через точку b линию действия вектора вращательной скорости 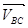 перпендикулярно звену В3С3, а из полюса PV3 параллельно траектории точки С3 при поступательном движении проводим линию действия вектора абсолютной скорости
перпендикулярно звену В3С3, а из полюса PV3 параллельно траектории точки С3 при поступательном движении проводим линию действия вектора абсолютной скорости 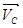 до пересечения с линией действия вектора скорости
до пересечения с линией действия вектора скорости 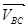 в точке с. Отрезок
в точке с. Отрезок 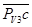 соответствует абсолютной скорости точки С, отрезок
соответствует абсолютной скорости точки С, отрезок 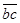 - вращательной скорости точки С вокруг В. Модули этих скоростей:
- вращательной скорости точки С вокруг В. Модули этих скоростей:
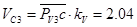 м/с
м/с
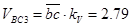 м/с
м/с
Направления векторов скоростей 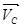 и
и 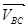 определяются согласно векторному уравнению (1.16).
определяются согласно векторному уравнению (1.16).
Для определения какой-либо промежуточной точки звена (центра тяжести S2 звена ВС) используют свойство подобия:
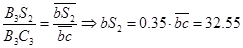 мм
мм
Отрезок 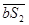 откладываем на плане скоростей от точки b в такую сторону, чтобы последовательность точек на звене ВС соответствовала последовательности точек на плане скоростей. Соединив точку S2 c полюсом плана, получим отрезок
откладываем на плане скоростей от точки b в такую сторону, чтобы последовательность точек на звене ВС соответствовала последовательности точек на плане скоростей. Соединив точку S2 c полюсом плана, получим отрезок 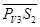 , соответствующий в масштабе плана скоростей скорости точки S2.
, соответствующий в масштабе плана скоростей скорости точки S2.
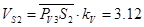 м/с
м/с
Аналогично находится модуль точки S1:
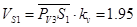 м/с
м/с
Скорость точки А, принадлежащей кривошипу 1 и стойке, равна нулю, и на плане скоростей будет совпадать с полюсом плана скоростей.
На основании плана скоростей находим мгновенное значение модуля и направления угловой скорости w2 шатуна. Согласно уравнению (1.14) модуль угловой скорости:
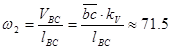 1/с
1/с
Для определения направления угловой скорости w2 вектор скорости 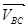 с плана скоростей мысленно переносится в точку С и увязывается направление вращательной скорости
с плана скоростей мысленно переносится в точку С и увязывается направление вращательной скорости 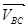 с направлением угловой скорости w2 шатуна.
с направлением угловой скорости w2 шатуна.
Аналогичным образом строятся остальные планы скоростей и находятся скорости точек:
VBС1=2,25 м/с VC1=2,76 м/с
VBС2= VC2=
VBС4= VC4=
VBС5=2,79 м/с VC5=3,6 м/с
VBС6= VC6=
VBС7=3,12 м/с VC7=4,02 м/с
VBС0= VC0=
Построение плана ускорений.
План ускорений позволяет определить линейное ускорение любой точки всех звеньев, угловое ускорение звеньев является основой для вычисления инерционных факторов в силовом расчете механизма.
Точка В описывает криволинейную траекторию, следовательно, полное (абсолютное) ускорение складывается из двух составляющих:
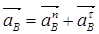 (1.18)
(1.18)
где 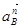 - вектор нормального (центростремительного) ускорения
- вектор нормального (центростремительного) ускорения
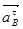 - вектор касательного ускорения
- вектор касательного ускорения
Модуль касательного ускорения:
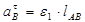 (1.19)
(1.19)
где e1 – угловое ускорение кривошипа 1.
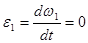 , т.к. по условию w1= const
, т.к. по условию w1= const
Следовательно, полное ускорение точки В:
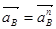 (1.20)
(1.20)
Модуль нормального ускорения:
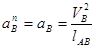 (1.21)
(1.21)
В нашем случае 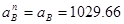 м/с2. Линия действия ускорения
м/с2. Линия действия ускорения 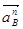 совпадает с радиусом (звеном 1 - кривошипом), и направленно это ускорение к центру вращения (полюсу).
совпадает с радиусом (звеном 1 - кривошипом), и направленно это ускорение к центру вращения (полюсу).
На основании предыдущего раздела 1.5.3. абсолютное ускорение точки С:
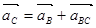 (1.22)
(1.22)
где 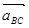 - ускорение точки С во вращательном движении звена ВС вокруг полюса В.
- ускорение точки С во вращательном движении звена ВС вокруг полюса В.
Ускорение точки С по аналогии с уравнением (1.18) может быть представлено в виде сумм двух составляющих:
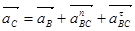 (1.23)
(1.23)
где 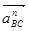 - вектор нормального ускорения точки С в ее вращательном движении
- вектор нормального ускорения точки С в ее вращательном движении
вокруг полюса В.
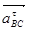 - вектор касательного ускорения
- вектор касательного ускорения
Модуль нормального ускорения по аналогии с уравнением (1.21):
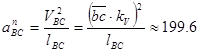 м/с2
м/с2
Линия действия вектора 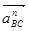 совпадает с шатуном 2, направленно это ускорение к точке В1.
совпадает с шатуном 2, направленно это ускорение к точке В1.
Для вектора касательного ускорения 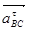 известна только линия действия, расположенная перпендикулярно нормальному ускорению
известна только линия действия, расположенная перпендикулярно нормальному ускорению 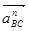 , т.е. звену ВС. Точка С совершает поступательное движение вместе с ползуном, поэтому линия действия полного ускорения
, т.е. звену ВС. Точка С совершает поступательное движение вместе с ползуном, поэтому линия действия полного ускорения 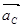 параллельна траектории точки С при поступательном движении. Уравнение (1.23) содержит две неизвестных величины, поэтому его можно решить графическим путем.
параллельна траектории точки С при поступательном движении. Уравнение (1.23) содержит две неизвестных величины, поэтому его можно решить графическим путем.
Возьмем за полюс плана ускорений точку Pa3, а отрезок 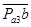 пусть будет равен 150 мм (длина отрезка, соответствующая на плане ускорений ускорению точки В). Тогда масштаб плана ускорений:
пусть будет равен 150 мм (длина отрезка, соответствующая на плане ускорений ускорению точки В). Тогда масштаб плана ускорений:
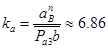
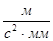
Длина отрезка, изображающая на плане ускорений ускорение 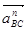 :
:
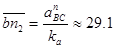 мм
мм
Из полюса ускорений Pa3 проводим луч параллельный звену АВ3, и на нем в направлении к точке А откладываем отрезок 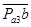 , соответствующий ускорению точки В. Из конца этого отрезка – точки В – проводим луч и откладываем на нем в сторону точки В3 отрезок
, соответствующий ускорению точки В. Из конца этого отрезка – точки В – проводим луч и откладываем на нем в сторону точки В3 отрезок 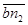 , соответствующий, согласно уравнению (1.23), вектору ускорения
, соответствующий, согласно уравнению (1.23), вектору ускорения 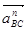 . Перпендикулярно отрезку
. Перпендикулярно отрезку 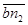 проводим луч, а из полюса плана Pa3 проводим другой луч ло пересечения с первым в точке с. Длина отрезка
проводим луч, а из полюса плана Pa3 проводим другой луч ло пересечения с первым в точке с. Длина отрезка 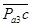 соответствует в заданном масштабе плана ускорению
соответствует в заданном масштабе плана ускорению 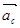 , отрезок
, отрезок 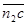 - ускорению
- ускорению  . Модули этих ускорений:
. Модули этих ускорений:
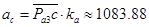 м/с2
м/с2
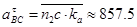 м/с2
м/с2
В соответствии с уравнением (1.23) показываем направления всех векторов ускорения.
Ускорения для промежуточных точек определяются по свойству подобия. 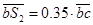 , а
, а 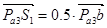 . Таким образом
. Таким образом 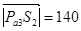 мм. Откуда получим:
мм. Откуда получим:
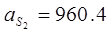 м/с2
м/с2
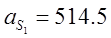 м/с2
м/с2
Модуль углового ускорения шатуна 2 можно вывести из формулы (1.19):
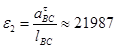 1/с2
1/с2
Перенесем вектор ускорения 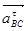 с плана ускорений в точку С3 плана механизма, и увидим, что угловое ускорение e2 направлено против часовой стрелки.
с плана ускорений в точку С3 плана механизма, и увидим, что угловое ускорение e2 направлено против часовой стрелки.
 2020-01-14
2020-01-14 171
171








