Действительно, из (16´) и (17´) имеем:
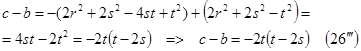
Учитывая (14) и (19´), можно получить разность  другим способом:
другим способом:
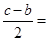
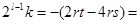 -
-  =>
=>  .
.
Следовательно, - 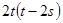 =-
=-  => 2t = 4r (
=> 2t = 4r ( ≠ 0, т.к.в (26´´) с ≠ b ) => t = 2r (32´) => в (16´) и (17´) c и b – четные, чего не должно быть.
≠ 0, т.к.в (26´´) с ≠ b ) => t = 2r (32´) => в (16´) и (17´) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
********
Случай 11
 (16)
(16)
 (17)
(17)
 (18)
(18)
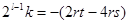 (19´)
(19´)
Из (16) и (17) имеем:
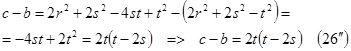
Учитывая (14) и (19´), можно получить разность  другим способом:
другим способом:

 -
-  =>
=>  .
.
Следовательно, 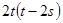 =-
=-  => 2t = - 4r (
=> 2t = - 4r (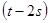 ≠ 0, т.к.в (26´´) с ≠ b ) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
≠ 0, т.к.в (26´´) с ≠ b ) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
Случай 12
 (16´)
(16´)
 (17´)
(17´)
 (18´)
(18´)
 (19),
(19),
т.е. по сравнению с предыдущим случаем 11 здесь знаки перед скобками противоположные, а потому (по понятным причинам) результат будет таким же, что и в случае 11.
Действительно, из (16´) и (17´) имеем:
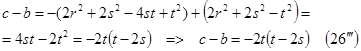
Учитывая (14) и (19), можно получить разность  другим способом:
другим способом:


 =>
=>  .
.
Следовательно, -  =
=  => 2t = - 4r (
=> 2t = - 4r ( ≠ 0, т.к.в (26´´) с ≠ b ) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
≠ 0, т.к.в (26´´) с ≠ b ) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
*******
Случай 13
 (16)
(16)
 (17)
(17)
 (18´)
(18´)
 (19´)
(19´)
Из (16) и (17) имеем:

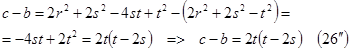
Учитывая (14) и (19´), можно получить разность  другим способом:
другим способом:

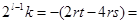 -
-  =>
=>  .
.
Следовательно,  =-
=-  => 2t = - 4r (
=> 2t = - 4r (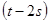 ≠ 0, т.к.в (26´´) с ≠ b ) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
≠ 0, т.к.в (26´´) с ≠ b ) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
********
Случай 14
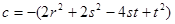 (16´)
(16´)
 (17´)
(17´)
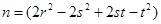 (18)
(18)
 (19),
(19),
т.е. по сравнению с предыдущим случаем 13 здесь знаки перед скобками противоположные, а потому (по понятным причинам) результат будет таким же, что и в случае 13.
Действительно, из (16´) и (17´) имеем:

Учитывая (14) и (19), можно получить разность  другим способом:
другим способом:


 =>
=>  .
.
Следовательно, - 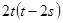 =
= 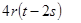 => 2t = - 4r (
=> 2t = - 4r (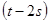 ≠ 0, т.к.в (26´´) с ≠ b ) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
≠ 0, т.к.в (26´´) с ≠ b ) => t = -2r (32´) => в (16) и (17) c и b – четные, чего не должно быть.
Мы пришли к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
***********
Вывод.
1. Таким образом, случаи 9,…, 14 новых возможных решений уравнения (15) не выявили.
2. Условие 1 (продолжение) нами полностью рассмотрено.
**********
Условие 2 (продолжение).
Ранее мы отмечали, что уравнение (15) симметрично для с и b, поэтому с и b могут меняться своими выражениями (C и В). Это свойство нами было названо «новым свойством  ».
».
В 1-й части Утверждения 1 мы рассмотрели два «Новых» случая «+» и «-».
Осталось исследовать еще 14 случаев,рассматривающих «новые свойства  », когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
», когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
********
«Новый» случай 15
( Отличающийся «новым свойством  » от случая 1: с = С, b = -В, n = N,
» от случая 1: с = С, b = -В, n = N,  K)
K)
с = - В ( 16-B ) ,
b = С ( 17+C),
n = N ( 18 ),
 K ( 19 ) - это общие решения уравнения (15), окончательным видом которых являются (это мы покажем далее) окончательные решения уравнения (15) в случае 8, т.е.
K ( 19 ) - это общие решения уравнения (15), окончательным видом которых являются (это мы покажем далее) окончательные решения уравнения (15) в случае 8, т.е.
 (40´),
(40´),  (38´´),
(38´´),
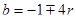
 ,
,  (33),
(33),
где  - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
Доказательство
Сумма  имеет вид:
имеет вид:

Учитывая (14) и (19), можно получить разность  :
:


 =>
=>  .
.
Выразим из (25) и (26)  :
:
 =>
=> 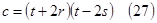
 =>
=> 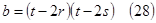 .
.
По условию  должны быть взаимно простыми целыми числами, поэтому их общий множитель
должны быть взаимно простыми целыми числами, поэтому их общий множитель  .
.
Т.о.,  имеют вид:
имеют вид:
 ,
,  , а их сумма
, а их сумма  .
.
Т.к. из (8)  , то
, то  =>
=> 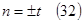 .
.
Из (19) с учетом (29) выразим  :
:
 , т.е.
, т.е. 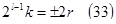 .
.
Т.о.,  ,
,  , т.е.
, т.е.

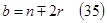 , выражения которых, с учетом (33), полностью совпадают с (9) и (10).
, выражения которых, с учетом (33), полностью совпадают с (9) и (10).
Теперь найдем сумму с  :
:
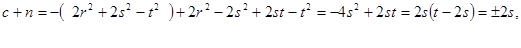
т.к.  , т.е.
, т.е.  .
.
(Здесь чередование «плюса» и «минуса» такое же, как и у единицы в (29). В последующих действиях мы это учтем).
Теперь, учитывая (32), получим значение для с:
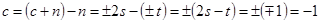 ,
,
т.к. из (29) вытекает 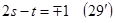 .
.
Итак,  .
.
Учитывая (34), получим 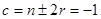 =>
=>  .
.
Теперь, с учетом (38´´), можно получить окончательное выражение для b (из (35)):
 , т.е.
, т.е.  .
.
Таким образом, уравнение  (15), решениями которого являются (16-B), (17+C), (18) и (19), в конечном счете имеет следующие решения (являющиеся окончательными решениями в случае 8):
(15), решениями которого являются (16-B), (17+C), (18) и (19), в конечном счете имеет следующие решения (являющиеся окончательными решениями в случае 8):



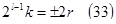 , где
, где  - взаимно простые нечетные целые числа, ч.т.д.
- взаимно простые нечетные целые числа, ч.т.д.
*********
Примечание
То, что окончательные решения в случаях 15 и 8 одинаковые, вытекает и из следующего соображения, которое используем в дальнейшем (для быстроты суждений).
Случай 15. Случай 8
с = - В ( 16-B ), с = - С ( 16´ ) ,
b = С ( 17+C), b = В ( 17),
n = N ( 18 ), n = N ( 18 ),
 K ( 19 ),
K ( 19 ),  K ( 19 ).
K ( 19 ).
У этих случаев одинаковые знаки в правых частях с и b, но разные выражения (С и В), в остальном эти случаи похожи.
Соображение
Если в этих случаях решения совпадают, значит, у них надо выявить что-то общее. Этим общим свойством для них являются произведение и разность с и b.
«Общие свойства для с и b »:
сb= -СВ, с – b= -С -В, с – b= 2К 
Воспользуемся свойствами корней квадратного уравнения (теоремой Виета). Имеем:
с (- b ) = СВ, с+ (– b ) = -С -В = 2К.
Отсюда получаем квадратное уравнение
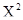 - 2К
- 2К  + С В = 0 => X1,2 = К
+ С В = 0 => X1,2 = К 
 ,
,
где, например, Х1 = - b, а Х2 = с, то есть
Х1 = - b = К +  =
=  +
+ 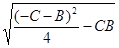 =
=  +
+  =
=  +
+  = -В => b = В,
= -В => b = В,
где на основании 
 и Х1 = - b= -
и Х1 = - b= - 
Х2= с = К-  =
=  -
-  =
=  -
-  =
=  -
-  = -С => с = - С,
= -С => с = - С,
где на основании (40´)  и Х2 =
и Х2 =  Таким образом, мы получили случай 8:
Таким образом, мы получили случай 8:
Случай 8
с = - С ( 16´ ) ,
b = В ( 17),
n = N ( 18 ),
 K ( 19 ),
K ( 19 ),
где



 , а
, а  - взаимно простые нечетные целые числа.
- взаимно простые нечетные целые числа.
Теперь обозначим Х1 = с, а Х2 = - b. Тогда получим:
Х1 = с = К+  =
=  +
+ 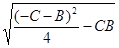 =
=  +
+  =
=  +
+  = -В => с = -В,
= -В => с = -В,
где на основании (40´) 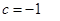 и Х1 = с = -1.
и Х1 = с = -1.
Х2 = - b = К-  =
=  -
- 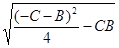 =
=  -
-  =
=  -
-  = -С => - b = -С => b = С,
= -С => - b = -С => b = С,
где на основании 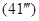
 и Х 2 = -
и Х 2 = - 
Таким образом, мы получили случай 15:
Случай 15
с = -В ( 16-B ) ,
b = С ( 17+C),
n = N ( 18 ),
 K ( 19 ),
K ( 19 ),
где

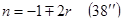
 2020-01-14
2020-01-14 97
97








