Работа Скворцова Александра Петровича,
Учителя, ветерана педагогического труда
Доказательство утверждения, частным случаем которого является великая теорема Ферма
Содержание
Общее утверждение
Утверждение 1
Доказательство Части первой «Утверждения 1»
Доказательство Части второй «Утверждения 1»
Пример
Примечание
«Вывод» о Великой теореме Ферма (простое)
Утверждение 2
Доказательство Части первой «Утверждения 2»
Доказательство Части второй «Утверждения 2»
Примечание
Окончательный «Вывод» о Великой теореме Ферма
Утверждение 3
Доказательство Части первой «Утверждения 3»
Доказательство Части второй «Утверждения 3»
Примечание
Общий вывод
Литература
Доказательство нижеприведённого «Утверждения» осуществлено элементарными средствами. В данной работе рассматриваются уравнения  , частными случаями которых являются уравнения Ферма
, частными случаями которых являются уравнения Ферма  , где а – чётное число,
, где а – чётное число,  и
и  - целые числа,
- целые числа,  ,
,  ,
,  - =натуральные числа.
- =натуральные числа.
Метод, используемый в этой работе, опирается на применение дополнительного квадратного уравнения 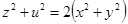 и его общего решения, чётность которого совпадает с числами, исследуемыми в моей работе.
и его общего решения, чётность которого совпадает с числами, исследуемыми в моей работе.
Этот метод позволяет:
1. Судить о возможности существования целых решений уравнения Ферма для  , т.е. о возможности существования «Пифагоровых троек», т.к. при рассуждениях никаких «противоречий» не возникает (доказательство этого в данной работе не приведено).
, т.е. о возможности существования «Пифагоровых троек», т.к. при рассуждениях никаких «противоречий» не возникает (доказательство этого в данной работе не приведено).
2. Судить об отсутствии решений в попарно взаимно простых целых числах уравнения  , где
, где  - натуральное число, а – чётное число, т.к. при рассуждениях возникают «противоречия» (доказательство этого в данной работе не приведено, но дан пример на стр. 33).
- натуральное число, а – чётное число, т.к. при рассуждениях возникают «противоречия» (доказательство этого в данной работе не приведено, но дан пример на стр. 33).
3. Судить о возможности существования частного решения уравнения  при
при  ( илиb = ±1, или c = ±1 ), которое входит в п. «Исключения» моего общего «Утверждения». И такие решения следующие:
( илиb = ±1, или c = ±1 ), которое входит в п. «Исключения» моего общего «Утверждения». И такие решения следующие:
а) b = ±1; c = ±3; a = 2.
б) b =  3; c = ±1; a = -2 («Пример» на стр. 33).
3; c = ±1; a = -2 («Пример» на стр. 33).
4. Судить о неразрешимости в целых числах уравнения  , где а – чётное число. Это хорошо известный факт в теории чисел (доказательство этого в данной работе приведено).
, где а – чётное число. Это хорошо известный факт в теории чисел (доказательство этого в данной работе приведено).
5. Судить о неразрешимости в целых числах и уравнения Ферма  . Это тоже хорошо известный факт в теории чисел (в данной работе это утверждение является следствием более общего утверждения).
. Это тоже хорошо известный факт в теории чисел (в данной работе это утверждение является следствием более общего утверждения).
6. Судить о неразрешимости в целых числах уравнения Ферма  , где
, где  - натуральное число. Это тоже уже известный факт в теории чисел (в данной работе это утверждение является следствием более общего утверждения).
- натуральное число. Это тоже уже известный факт в теории чисел (в данной работе это утверждение является следствием более общего утверждения).
**********
Так как данное доказательство «Общего Утверждения» в этой работе проведено мною элементарными средствами, то думаю, и своё «Утверждение» великий Ферма вполне мог доказать подобным методом.
И последнее. Я думаю, что специалистам, наверное, известны ещё некоторые конкретные примеры (частные случаи уравнения  ), подпадающих под доказываемое в данной работе «Общего Утверждения». Если такие примеры имеются, то в свою очередь это будет являться дополнительным подтверждением правильности выбранного пути доказательства вышеназванного «Общего Утверждения».
), подпадающих под доказываемое в данной работе «Общего Утверждения». Если такие примеры имеются, то в свою очередь это будет являться дополнительным подтверждением правильности выбранного пути доказательства вышеназванного «Общего Утверждения».
≥
ОБЩЕЕ УТВЕРЖДЕНИЕ, частным случаем которого является Великая теорема Ферма
1. Уравнение  (
( ,
,  - натуральные числа) не имеет решений в отличных от нуля попарно взаимно простых целых числах
- натуральные числа) не имеет решений в отличных от нуля попарно взаимно простых целых числах  ,
,  и
и  таких, чтобы
таких, чтобы  - было четным,
- было четным,  и
и  - нечетными целыми числами.
- нечетными целыми числами.
2. Но есть и «исключение» из данного утверждения: среди этих чисел 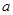 ,
,  и
и  может быть либо
может быть либо  , либо
, либо  .
.
***********
Чтобы доказать «ОБЩЕЕ УТВЕРЖДЕНИЕ», необходимо рассмотреть2 случая
для показателя q:
1)  при
при  - натуральном;
- натуральном;
2) 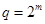 при
при  - натуральном, а для этого достаточно рассмотреть случай
- натуральном, а для этого достаточно рассмотреть случай  .
.
Утверждение 1, частным случаем которого является Великая теорема Ферма, для простого показателя 
Часть 1
Уравнение  (
( ,
,  - натуральные числа, где
- натуральные числа, где  при
при  - натуральном) не имеет решений в отличных от нуля попарно взаимно простых целых числах
- натуральном) не имеет решений в отличных от нуля попарно взаимно простых целых числах  ,
,  и
и  таких, чтобы
таких, чтобы  - было четным,
- было четным,  и
и  - нечетными целыми числами.
- нечетными целыми числами.
Часть 2
Возможны случаи: либо  , либо
, либо  .
.
**********
Последнее утверждение (либо  , либо
, либо  ) в дальнейшем будем называть «исключением» из общего правила.
) в дальнейшем будем называть «исключением» из общего правила.
*********
Часть первая (Утверждения 1)
Уравнение  (
( ,
,  - натуральные числа, где
- натуральные числа, где 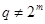 при
при  - натуральном) не имеет решений в отличных от нуля попарно взаимно простых целых числах
- натуральном) не имеет решений в отличных от нуля попарно взаимно простых целых числах  ,
,  и
и  таких, чтобы
таких, чтобы  - было четным,
- было четным,  и
и  - нечетными целыми числами.
- нечетными целыми числами.
Доказательство
Понятно, что доказательство достаточно рассмотреть для  - простого.
- простого.
Докажем данное «Утверждение 1» методом от противного. Предположим, что уравнение  разрешимо в отличных от нуля попарно взаимно простых целых числах
разрешимо в отличных от нуля попарно взаимно простых целых числах  ,
,  и
и  . И если в конце доказательства мы придем к противоречию, доказав, что числа
. И если в конце доказательства мы придем к противоречию, доказав, что числа  ,
,  и
и  не являются попарно взаимно простыми целыми числами, то это будет означать, что «Утверждение 1» справедливо.
не являются попарно взаимно простыми целыми числами, то это будет означать, что «Утверждение 1» справедливо.
Из уравнения (1) следует:
 (2),
(2),
где  - четное целое число, т.к.
- четное целое число, т.к.  и
и  - нечетные;
- нечетные;
 ≠ 0, т.к.
≠ 0, т.к.  и
и  - взаимно простые нечетные целые числа, не равные нулю;
- взаимно простые нечетные целые числа, не равные нулю;
 - нечетное целое число при
- нечетное целое число при  и
и  - нечетных,
- нечетных,  - простом.
- простом.
********
Примечание
То, что  - нечетное число при
- нечетное число при  и
и  - нечетных, хорошо известный факт в теории чисел.
- нечетных, хорошо известный факт в теории чисел.
Для подтверждения данного факта достаточно использовать разложение бинома
Ньютона  ,
,  ,
,  , … и тогда получим для
, … и тогда получим для  :
:
 - сумму трех нечетных слагаемых, равную нечетному числу.
- сумму трех нечетных слагаемых, равную нечетному числу.
Для 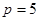 :
:
 - сумму пяти нечетных слагаемых, равную нечетному числу.
- сумму пяти нечетных слагаемых, равную нечетному числу.
Для степени  - простой можно доказать, что при
- простой можно доказать, что при  и
и  нечетных
нечетных
(3)  - сумма нечетных
- сумма нечетных  слагаемых, равная нечетному числу (Алексеев С.Ф. Два обобщения классических формул // Квант. – 1988. - №10. – С. 23).
слагаемых, равная нечетному числу (Алексеев С.Ф. Два обобщения классических формул // Квант. – 1988. - №10. – С. 23).
*******
Пусть  (4),
(4),
где  - нечетное число (на основании (3)).
- нечетное число (на основании (3)).
Тогда уравнение (2) примет вид:
 (5),
(5),
где 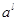 - четное число, которое можно представить в виде
- четное число, которое можно представить в виде
 (6),
(6),
где  - целое число (при
- целое число (при  = 0 а = 0, что противоречит нашему допущению),
= 0 а = 0, что противоречит нашему допущению),
 (4) – нечетное число.
(4) – нечетное число.
Тогда из соотношения (5) с учетом (6) получаем:
 , т.е.
, т.е.  (7), где
(7), где  - целое число (
- целое число ( ),
),  - натуральное число.
- натуральное число.
Сумму же нечетных чисел  и
и  обозначим через
обозначим через  , т.е.
, т.е.
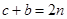 (8),
(8),
где  - целое число (
- целое число (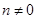 , т.к.
, т.к.  и
и  - взаимно простые нечетные целые числа, не равные нулю).
- взаимно простые нечетные целые числа, не равные нулю).
Из (7) и (8) определим  и
и  :
:
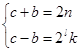 =>
=>  =>
=> 
Откуда (11)  - нечетное число при
- нечетное число при  - нечетном и
- нечетном и  - четном, т.к.
- четном, т.к.  , причем (12)
, причем (12)  (явно) при
(явно) при  .
.
********
Вывод:
На основании (8) и (11) имеем: (13) 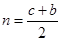 - нечетное число;
- нечетное число;
из соотношений (7) и (12) имеем: (14)  (явно) при
(явно) при  .
.
Это дополнительная информация о свойствах предполагаемых взаимно простых числах 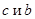 , которая в дальнейшем нам очень пригодится.
, которая в дальнейшем нам очень пригодится.
*******
Теперь попробуем выразить сумму квадратов чисел c и  . Учитывая соотношения (9) и (10), получим:
. Учитывая соотношения (9) и (10), получим:



Таким образом, получили следующее уравнение:
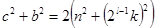 (15),
(15),
где 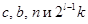 - целые числа, которые, являясь решениями уравнения (15), в свою очередь, могут быть выражены через другие целые числа
- целые числа, которые, являясь решениями уравнения (15), в свою очередь, могут быть выражены через другие целые числа  следующим образом:
следующим образом:
(16)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(17)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(18)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(19)  - четное число.
- четное число.
Примечание: во всех последующих исследованиях (Случаях) нас не будут интересовать
t =0 и r=0 (при t =0  и
и 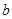 - четные из (16) и (17), при r=0
- четные из (16) и (17), при r=0  = 0 (из (19)) => а = 0 (из (6)), что противоречит нашему допущению).
= 0 (из (19)) => а = 0 (из (6)), что противоречит нашему допущению).
*******
Примечание.
Общий вид уравнения (15) следующий:
(20)  ,
,
целыми решениями которого (это известный факт в теории чисел) являются:
(21)  ;
;
(22)  ;
;
(23) 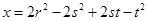 ;
;
(24)  , где
, где  - целые числа.
- целые числа.
То, что (21), …, (24) являются решениями уравнения (20), легко проверяется их подстановкой в данное уравнение (20), которое при этом превращается в тождество.
*******
Для простоты обозначим правые части уравнений (16), …, (19) буквами С, В, N, К, т.е.
 = С
= С
 = В
= В
 = N
= N
 = К,
= К,
и рассмотрим с лучай, когда в правых частях уравнений (16), …, (19) перед С, В, N, К, стоят «плюсы» и выполняется Условие 1.
Условие1 (начало).
с = С
b = B
n = N

Случай «+».
(16+)  = С - нечетное число при
= С - нечетное число при  - нечетном;
- нечетном;
(17+)  = В - нечетное число при
= В - нечетное число при  - нечетном;
- нечетном;
(18+)  = N - нечетное число при
= N - нечетное число при  - нечетном;
- нечетном;
(19+) 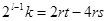 = К - четное число.
= К - четное число.
Казалось бы, все в порядке: четность  в (16+), …, (19+) совпадает при
в (16+), …, (19+) совпадает при  - нечетном с нашими предыдущими рассуждениями.
- нечетном с нашими предыдущими рассуждениями.
Однако не все так просто.
Помимо всего прочего, у нас есть еще две дополнительные информации (13) и (14) (о четности, заключенной в «Выводе» (стр.5)), вытекающие из предположения о том, что, вопреки условию «Утверждения 1», допустим, существуют попарно взаимно простые целые числа  .
.
Попробуем найти сумму  , воспользовавшись их выражениями (16+) и (17+):
, воспользовавшись их выражениями (16+) и (17+):
 ,
,
т.е.  пропорционально 4, откуда следует, учитывая (13) в «Выводе» (стр.5),
пропорционально 4, откуда следует, учитывая (13) в «Выводе» (стр.5),  !
!
Т.е., вопреки «Выводу», в Случае «+»  является не нечетным, а четным числом, что возможно (из (18+)) при
является не нечетным, а четным числом, что возможно (из (18+)) при 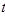 - четном.
- четном.
Однако, если  - четное, то
- четное, то  (в (16+) и (17+)) являются четными, т.е. в уравнениях (2) и (1) числа
(в (16+) и (17+)) являются четными, т.е. в уравнениях (2) и (1) числа  - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию в Случае «+» с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
 2020-01-14
2020-01-14 113
113







