· Необходимые и достаточные условия сходимости метода Ньютона:
 непрерывна на [a;b] и
непрерывна на [a;b] и  ;
;
 и
и 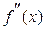 отличны от нуля и сохраняют знаки для
отличны от нуля и сохраняют знаки для  .
.
В нашем случае на отрезке [0;1] требования теоремы выполняются.
· Начальное приближение  должно удовлетворять условию:
должно удовлетворять условию:  , т.е. за начальное приближение следует принять тот конец отрезка, где знак функции и знак второй производной совпадают. Поскольку
, т.е. за начальное приближение следует принять тот конец отрезка, где знак функции и знак второй производной совпадают. Поскольку  < 0 и
< 0 и  < 0, то выберем начальное приближение к корню:
< 0, то выберем начальное приближение к корню:  =1.
=1.
· Условие окончания процесса уточнения корня. Для оценки погрешности метода Ньютона справедливо соотношение:  , где M2 – наибольшее значение
, где M2 – наибольшее значение  , m1 –наименьшее значение
, m1 –наименьшее значение  на отрезке[a;b]. Из требования обеспечения точности следует условие окончания вычислений
на отрезке[a;b]. Из требования обеспечения точности следует условие окончания вычислений 
Ручной расчет» трех итераций
Для получения решения уравнения методом Ньютона воспользуемся следующей рекуррентной формулой: 
В нашем случае  ,
,  =1
=1


 
 
 
 
|
Представим вычисления в виде следующей таблицы 1-2b.
| k | Xk | f(xk) |
| 0 | 1 | -1.4597 |
| 1 | 0.6200 | -4.62•10-2 |
| 2 | 0.607121 | -6. 788 •10-5 |
| 3 | 0.607102 | -1.484 •10-10 |
Погрешность численного решения нелинейных уравнений
Оценим погрешность после трех итераций:



Тогда  .
.
Метод хорд
 2020-01-14
2020-01-14 186
186








