1. Задание для численного решения обыкновенных дифференциальных уравнений:
· дифференциальное уравнение 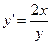 ;
;
· интервал [1;6];
· начальные условия x0=1, y0=1;
· шаг интегрирования h=0.5
Точное аналитическое решение заданного дифференциального уравнения
Найдем точное аналитическое решение заданного дифференциального уравнения y(x) методом разделения переменных.

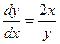
Запишем уравнение в виде  и проинтегрируем обе части равенства с учетом начальных условий.
и проинтегрируем обе части равенства с учетом начальных условий.
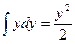 ;
; 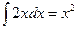
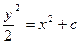
Из начальных условий найдем константу c:
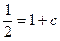 , следовательно
, следовательно 
То есть 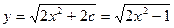
Таким образом, аналитическое (точное) решение дифференциального уравнения 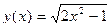
Значения точного решения ОДУ – y(x)
Вычислим значения полученного решения y(xi), где  ,
,  на отрезке [1;6] с шагом изменения аргумента h=0.5:
на отрезке [1;6] с шагом изменения аргумента h=0.5:


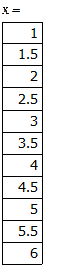 
|
 2020-01-14
2020-01-14 128
128








