Вопросы, подлежащие изучению

1. Постановка задачи численного решения обыкновенных дифференциальных уравнений. Задача Коши.

2. Методы Рунге-Кутты различных порядков, общие свойства.

3. Погрешности методов Рунге-Кутты.

4. Выбор шага интегрирования обыкновенных дифференциальных уравнений.

5. Графическая иллюстрация методов Рунге-Кутты.

 

Задание

1. Выбрать индивидуальное задание из табл.4-1 для решения обыкновенных дифференциальных уравнений:

· дифференциальное уравнение ;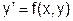

· интервал [a;b], где ищется решение дифференциального уравнения;

· начальные условия x₀, y₀;

· шаг интегрирования h _.

2. Найти аналитическое решение y(x) заданного дифференциального уравнения, полагая его точным.

3. Вычислить значения полученного решения 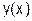 на отрезке [a;b] с шагом h.

4. Найти численное решение дифференциального уравнения методом Эйлера – функцию ye(x) в первых 4-х точках отрезка [a;b] с шагом h «расчетом вручную» (можно использовать математический пакет только как калькулятор). Оценить погрешности полученного решения по методу двойного просчета (правилу Рунге).

5. Найти численное решение дифференциального уравнения методом Эйлера – функцию y1(x) во всех точках отрезка [a;b] с шагом h, используя математический пакет.

6. Найти численное решение дифференциального уравнения методом Рунге-Кутты 2 порядка – функцию y2(x) в точках отрезка [a;b] с шагом h, используя математический пакет.

7. Найти численное решение дифференциального уравнения методом Рунге-Кутты 4 порядка – функцию y4(x) в точках отрезка [a;b] с шагом h, используя математический пакет.

Вычислить значения погрешностей численного решения дифференциального уравнения для каждого метода.

9. Графически проиллюстрировать полученные решения.

Варианты задания

                                Таблица 4-1

№ вар	Уравнение	x0	y0	h	a	b
1	y' = x y2	0	-2	0.4	0	4
2	y' = y2 (x2+ x + 1)	0	-2	0.2	0	2
3	y' = x3 y2	0	-2	0.2	0	2
4	y' = y / cos2(x)	0	1	0.1	0	1
5	y' = y cos(x)	0	1	0.5	0	5
6	y' = y2cos(x)	0	-1	0.4	0	4
7	y' = x2 y + y	0	1	0.2	0	2
8	y' = (x – 1)2 y2	0	-1	0.5	0	5
9	y' = x3 y	0	1	0.2	0	2
10	y' = y2 sin(x)	0	0.5	0.2	0	2
11	y' = y sin(x)	0	1	0.4	0	4
12	y' = x y	0	1	0.2	0	2
13	y' = y2 / x	1	1	0.2	1	2
14	y' = x2 y	0	1	0.2	0	2
15	y' = y2 (2 – x)	0	-1	0.4	0	4
16	y' = 3 x2 y2	0	-4	0.2	0	2
17	y' = y2 (ex + 4x)	0	-1	0.4	0	4
18	y' = y (x – 1)	0	1	0.4	0	4
19	y' = x (1 + y2)	0	0	0.2	0	1.6
20	y' = x / (2y)	0	1	0.4	0	4
21	y' = y / (3 x2)	1	1	0.2	1	3
22	y' = 4 x e-3y	1	0	0.2	1	3
23	y' = 2 x y	0	1	0.2	0	2
24	y' = 2 x (y1/2)	0	1	0.4	0	4
25	y' = y2 ex	0	-2	0.4	0	4
26	y' = x (1 – y2)1/2	0	0	0.4	0	1.6
27	y' = (1 + x) y	0	1	0.2	0	2
28	y' = x2 (1 – y2)1/2	0	0	0.4	0	1.6
29	y' = (x2 + x) y2	0	-1	0.4	0	4
30	y' = y2 / cos2(x)	0	-1	0.3	0	1.5
31	y' = y2sin x	0	1	0.1	0	1
32	y' = cos(x) y	0	1	0.1	0	1
33	y' =	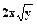0	1	0.1	0	1
34	y' = (x-1)2 y2	0	1	0.1	0	1
35	y' = y2 cos(x)	0	-1	0.1	0	1
36	y' = 0.5 y2	1	1	0.1	1	2
37	y' =  y2 x	0	-2	0.1	0	1
38	y' =	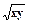3	3	0.1	3	4
39	y' = y2 ex	1	-1	0.1	1	2
40	y' = e-y	1	0	0.1	1	2

Содержание отчета

1. Индивидуальное задание.

2. Решение ОДУ аналитическим методом.

3. Значения полученного аналитического решения y(x) на отрезке [a;b] с шагом h

4. «Ручной расчет» численного решения ОДУ методом Эйлера – функция ye(x) в первых 4-х точках заданного отрезка [a;b] с шагом h и оценка погрешностей полученного решения по методу двойного просчета (правилу Рунге).

5. Значения численного решения ОДУ, вычисленные методом Эйлера – функция y1(x) во всех точках заданного отрезка [a;b] с шагом h _, используя математический пакет.

6. Значения численного решения ОДУ, вычисленные методом Рунге-Кутты 2 порядка – функция y2(x) во всех точках заданного отрезка [a;b] с шагом h _, используя математический пакет.

7. Значения численного решения ОДУ, вычисленные методом Рунге-Кутты 4 порядка – функция y4(x) во всех точках заданного отрезка [a;b] с шагом h _, используя математический пакет.

8. Вычисленные значения погрешностейчисленного решения дифференциального уравнения для каждого метода.

9. Графическая иллюстрация полученных решений.