Распознавание полимером поверхности

Ряд недавних статей посвящен изучению вопроса, может ли сополимер распознавать поверхность [3, 4, 12, 14], в том смысле, может ли он на большой поверхности выделить определенный участок и адсорбироваться именно на нем. В перспективе такого рода адсорбция может позволить передавать «узор» поверхности на любое заданное расстояние.

Одной из первых работ в этой области является работа Томаса Богнера, Андреаса Дегенхарда и Фридерики Шмид [3], посвященная молекулярному распознаванию сополимерами химически структурированной поверхности. Было обнаружено, что для успешного распознавания поверхности ее узор должен отвечать некоторым требованиям, так, например, он должен содержать предпочтительно гидрофобные, притягивающие звенья сайты во внутренней части. С другой стороны, оптимальные с точки зрения адсорбции на заданной поверхности сополимеры могут обладать существенно различными составами и распределениями звеньев по составу. Более того, близость последовательностей не всегда означает близость их способностей к преимущественной адсорбции, т.е. распознаванию.

Одной из последних работ, посвященной теме распознавания узора сополимером и передачи его на расстояние, является статья [4], посвященная компьютерному изучению передачи узора, находящегося на диблок сополимерной пленке, которая адсорбируется на химически неоднородной поверхности. Авторы изучали, как пленка может перенимать специфический узор поверхности, и затем использовали методы компьютерного моделирования для создания узора, который поможет адсорбирующейся пленке содержать этот узор. Они также изучили эффекты, связанные с изменением длины сополимера, размера пластинки с узором, и расстояния от поверхности с узором, и влияющие на расстояние, на которое узор может передаться. Целью их работы являлось понимание того, как узор на сополимерной пленке на определенном расстоянии от поверхности проникает через адсорбированную пленку на адсорбирующую неоднородную поверхность. Система изучалась с помощью метода Монте-Карло. Авторы обнаружили, что при увеличении расстояния от подложки, где находится целевой узор, передача узора уменьшается для всех узоров и всех длин цепей. При постоянном размере узора на подложке, передача узора на поверхность увеличивается с увеличением длины цепи. В случае одной длины цепи хорошо передаются узоры, при которых цепь принимает значение энергии, близкое к значению энергии, характерному для цепи в случае, если бы не было узорчатой поверхности.

Распознавание полимером поверхности представляет огромный интерес. Тем не менее, этот вопрос в рамках наиболее простых (минимально достаточных) моделей еще только изучается. Целью данной работы является изучение процесса адсорбции сополимера из мономерных звеньев двух типов A и B, на неоднородной поверхности, состоящей из полосок двух типов A и B, притягивающих одноименные звенья и отталкивающие звенья другого типа, а также поиск таких последовательностей звеньев в сополимере, при которых они будут адсорбироваться лучше других на данной поверхности. Таким образом, ставится вопрос об изучении процесса распознавания сополимером поверхности. Здесь под распознаванием мы понимаем такую адсорбцию, когда сополимер, адсорбируясь на узорчатой поверхности, принимает уникальную конформацию, соответствующую основному состоянию и обусловленную геометрией и химическим строением узора. Модель такого процесса адсорбции было была предложена Ю.А. Криксиным, П.Г. Халатуром и А.Р. Хохловым в недавней работе [6]. Эта модель будет изложена в следующем разделе.

Модель.

Модель распознавания узора, используемая в данной задаче, была разработана Ю.А. Криксиным, П.Г. Халатуром, А.Р. Хохловым [6]. Они разработали статистическую механическую модель для изучения адсорбции блоксополимера, состоящего из звеньев двух типов A и B, на химически неоднородной поверхности. Поверхность состоит из полосок двух типов (A и B), которые по ширине равны между собой.

Для начала рассмотрим идеальный раствор гауссовых цепей, каждая из которых состоит из N мономеров, находящуюся в объеме V. Предположим, что мономеры цепи являются материальными точками массы m, расстояние между мономерами по цепи a. Гамильтониан, определяющий их взаимодействие со средой и друг с другом, представляет собой сумму двух потенциалов – первый потенциал описывает взаимодействие между соседними по цепи мономерами, обусловленное ковалентной связью, а второй описывает взаимодействие i -го мономера с внешним полем. Слагаемое 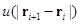 описывает взаимодействие соседних мономеров. Отметим, что в (3.1) отсутствуют члены, отвечающие взаимодействию исключенного объема, поэтому в этой модели возможны самопересечения цепи.

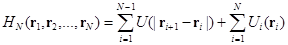                                    (3.1)

Также предположим, что ρ – это плотность мономеров. Тогда статистический интеграл такой цепи может быть записан в виде

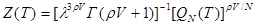,                                          (3.2)

где параметр 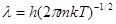 -это характеристическая длина. Здесь h – постоянная Планка, T – абсолютная температура, k – постоянная Больцмана. Г – это гамма функция, а правый множитель  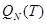обозначает статистический интеграл одиночной цепи, которая является интегралом по всем мономерам.

,                                                             (3.3)

где

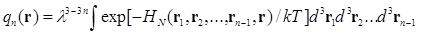           (3.4)

n=2,3…N, и .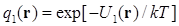

Здесь 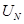 – потенциальная энергия цепи,  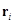– радиус-вектор, определяющий положение i -го мономера в пространстве. Для цепи конечной длины N можно написать рекуррентное соотношение для корреляционной функции 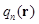, выражая ее через :

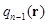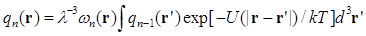                        (3.5)

где n=2,3…N, и .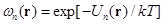

Теперь можно ввести следующую функцию:

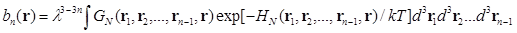(3.6)

где n=2,3…N, 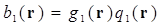 и

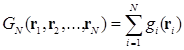                                                       (3.7)

где 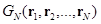 обозначает произвольную функцию, которая явно или неявно зависит от позиции вектора мономера N полимерной цепи. Таким образом, получилось, что

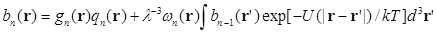    (3.8)

где n=2,3…N. Эти рекуррентные формулы положены в основу вычислительного алгоритма.

Физические свойства системы подсчитаны как статистические средние по всем возможным конфигурациям системы. В частности, все канонические средние могут быть написаны следующим образом:

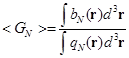                                                             (3.9)

Так, для свободной энергии системы, нормированной на количество мономерных звеньев, мы имеем

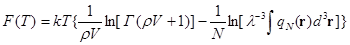                  (3.10)

Для дальнейших вычислений необходимо еще ввести ограничения. Так, поместим цепь в щель с периодическими границами по x и y направлениям, x=y=d, z=d_z (рис.1).

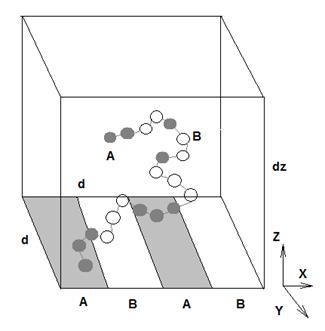
рис.1. схематическое представление модели системы.

Другими словами, эта система трансляционно инвариантна. Поверхности z = 0 и z = d_z являются отражающими поверхностями, причем поверхность z = 0 выбрана в качестве адсорбирующие поверхности. На ней находятся полосы одинаковой ширины ls и конечной длины. Каждая из этих полос химически однородна – каждая состоит из молекул типа A или типа B. Также рассматривается цепь, состоящая из мономеров двух типов A и B, причем они их количество зафиксировано так, что количество мономеров типа A равно количеству мономеров типа B. Для начала рассматривается система, в которой длина блока L_a = L_b = L, причем L << N. Такие полимеры могут рассматриваться как гомополимеры. Полная длина цепи – N = 2Lx, где x – это число диблоков A _L B _L. Вклад в последовательность характеризуется параметром σ_i = α (α = A или B), где i обозначает порядковый номер сегмента по цепи. В принципе, вклад в последовательность может быть изменен так, что могут быть определены различные полимерные структуры. Взаимодействие сополимера с адсорбирующей поверхностью определяется как распределением A или B сегментов по цепи, так и распределением полосок на поверхности, которые предполагаются составленными из двух химически различных видов адсорбционных полосок β (β = A или B), которые по-разному взаимодействуют с мономерами типа A или B.

Определим взаимодействие между соседними по цепи сегментами

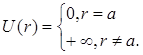                                                            (3.11)

Это потенциал, который отвечает свободно-сочлененной цепи, и для которого

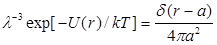                                              (3.12)

где 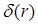 - это дельта-функция Дирака. Взаимодействие между i- сегментом цепи типа α (α = A или B) и двумя поверхностями z=0 и z=d_z описывается следующим образом:

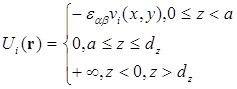                                       (3.13)

Здесь 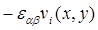 характеризует взаимодействие полимер-субстрат, которое зависит от положения i- ого сегмента по отношению к поверхности и 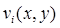- это аффинная функция, которую мы вводим как

                                               (3.14)

Считаем, что взаимодействие полимер-субстрат короткодействующее, то есть только если звенья цепи подогнаны к поверхности z=0, то они находятся под влиянием потенциала адсорбции. Взаимодействие 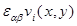 может вызывать как притяжение, так и отталкивание мономеров от полосы. Это взаимодействие зависит от вида мономера α и от вида полосы на поверхности β. Предполагается, что A и B сегменты адсорбируются преимущественно на полосах того же типа, и получается выигрыш в энергии ε_AA= ε_BB=ε, в то время как взаимодействие полимер A(B) и полоса B(A) является отрицательным ε_AB= ε_BA=-ε. В данной работе параметр ε предполагается неизменным, в то время как температуру kT можно менять. При низких температурах цепь адсорбируется на поверхности. При высоких температурах цепь просто находится в выделенном объеме.

Введем следующие функции:

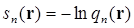                                                              (3.15)

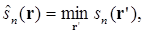
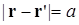                                            (3.16)

используя эти введенные функции и уравнение (3.12), получаем следующее выражение для рекуррентного соотношения (3.5)

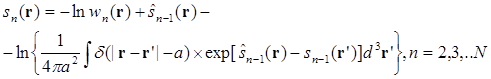(3.17)

где 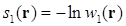. Тогда уравнение (3.3) перепишется в виде:

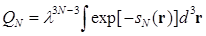.                                               (3.18)

Аналогично можно подсчитать интеграл в уравнении (3.8). Используя определение

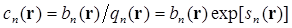,                              (3.19)

перепишем уравнение (3.8) как

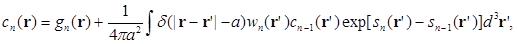 (3.20)

причем . Благодаря уравнениям (3.18) и (3.20) можно переписать уравнение (3.9) в следующей форме

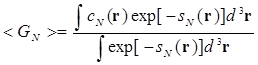.                                               (3.21)

Необходимо ввести некую систему сравнения. Наиболее разумным представляется выбор в качестве этой системы одиночной цепи, состоящей из звеньев одного типа (A), заключенная в ту же щель с такими же периодическими граничными условиями, около неадсорбирующей однородной поверхности, которой отвечает высокотемпературный режим.

Тогда различие в свободной энергии, приведенной на число мономеров в цепи, между изучаемой системой и системой, с которой производится сравнение, будет выражаться следующим образом

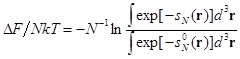
                                       (3.22)

где

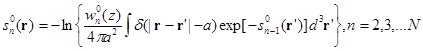    (3.23)

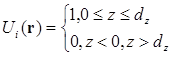                                                      (3.24)

и 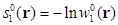 (это соответствует случаю, когда ε=0 в уравнении (3.13)).

Используя G_N функцию, определенную уравнением (3.7), можно подсчитать различные свойства цепи. В частности, предполагая, что g_i (r _i) = 1, если сегмент i находится в контакте с поверхностью z= 0, и g_i (r _i) = 0 в противоположном случае, средняя доля сегментов, которые находятся в контакте с субстратом выражается как

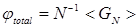.                                                            (3.25)

Для средней доли наиболее благоприятных контактов сегмент A/ полоса A и сегмент B/ полоса B можно написать:

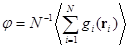,                                                              (3.26)

где

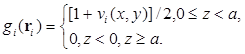                                    (3.27)

Следует заметить, что в отличие от φ _total, функция φ учитывает то, что сегмент A/ полоса A и сегмент B/ полоса B взаимодействия – это энергетически выгодные контакты, а взаимодействия типа сегмент A/ полоса B и сегмент B/ полоса A являются энергетически невыгодными контактами. Значения φ _total и φ лежат в пределах от 0 до 1.

Определяя функцию g_i (r _i) = u_i (r _i), где функция u_i (r _i) определяется из уравнения (3.13), можно найти внутреннюю энергию системы. Теплоемкость определяется как

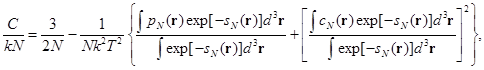(3.28)

где

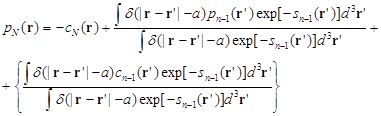           (3.29)

n =2,3…,N; .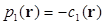

 

Методика вычислений.

В данной работе рассматриваются одиночная цепь, содержащая мономерные звенья двух типов A и B, адсорбирующаяся на неоднородной поверхности с полосами двух типов A и B. Система моделировалась с помощью метода Монте-Карло с модифицированным алгоритмом Метрополиса [6]. Этот метод является основным имитационным методом моделирования молекулярных систем, наряду с методом молекулярной динамики. Он состоит в следующем:

1. Генерируется первоначальная последовательность. В данной задаче в качестве первоначальной последовательности был выбран диблоксополимер, у которого первые N /2 звеньев являются звеньями  A, а последние N /2 - звеньями B. Рассчитывается энергия взаимодействия такой последовательности с поверхностью.

2. Случайным образом выбираются два мономерных звена. Эти звенья (их типы A и B) меняются местами.

3. Рассчитывается изменение в энергии: Δ F = F_new – F_old, где F_new – это энергия нового состояния (новой последовательности), а F_old – это энергия старого состояния (старой последовательности).

4. Если Δ F ≤0, то шаг принимается.

5. Если Δ F >0, то вычисляется величина 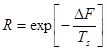, где T_s – это так называемая “температура мутации” (она отвечает за вероятность принятия новой последовательности в случае, если Δ F >0), а также выбирается случайное  число ξ, такое, что 0≤ξ≤1.

Если:

a. ξ≤ R, то новая последовательность принимается;

b. ξ> R, то эта последовательность не принимается, и остается старая последовательность.

6. Переходят на пункт 2.

Таким образом, метод Монте-Карло с модифицированным алгоритмом Метрополиса состоит в изменении последовательности мономерных звеньев так, чтобы получившаяся последовательность соответствовала наименьшим значениям свободной энергии взаимодействия сополимерной цепи с неоднородной поверхностью, состоящей из чередующихся полос А и В.

Необходимо отдельно обсудить роль “температуры мутации” T_s. Этот параметр, как уже было сказано выше, изменяет вероятность принятия таких последовательностей, для которых Δ F ≥0. Если этот параметр будет мал, то в результате параметр R также будет очень мал, и почти все цепи, для которых Δ F ≥0, приниматься не будут, что может привести к локальному минимуму, и не позволит перейти в другие состояния, поскольку вполне возможно, что для выхода цепи из локального на абсолютный минимум необходимо будет преодолеть некий потенциальный барьер. Если же “температура мутации” T_s будет большой, то параметр R будет порядка единицы, и все возможные перестановки будут приниматься.

Таким образом, возникает вопрос о нахождении оптимальной области изменения T_s, при которой эффективно и быстро находится абсолютный минимум (детально этот вопрос рассмотрен в пункте 5.1 данной работы). Отметим, что в данной задаче термодинамическая температура и “температура мутации” как и потенциальная и свободная энергии измеряются в энергетических единицах.

Сами вычисления состояли из двух этапов.

1. Первый этап состоял в поиске равновесной конформации. Как правило, на этом этапе было произведено 200 шагов по описанному выше алгоритму. После этого получившиеся  последовательности записывались и  исследовались дальше.

2. На втором этапе для всех уравновешенных последовательностей измерялись средние значения длины L_a блока из одноименных звеньев, свободной энергии F, потенциальной энергии U, доли адсорбированных звеньев φ и теплоемкости C _v по формулам, приведенным в пункте 3. Эти величины рассчитывались и усреднялись по 1000 последовательных конформаций.  

Результаты расчетов приведены в параграфе 5, в 6 разделе данной работы сделаны выводы.

Итак, мы рассмотрим адсорбцию сополимера из звеньев А и В на полосатой поверхности из чередующихся бесконечно длинных полосок А и В, каждая шириной ls.  В расчетах были изучены системы с ls =1, 2, 4, 8, 12, 16. A и B звенья адсорбируются преимущественно на полосах того же типа с выигрышем в энергии ε _AA = ε _BB = -1. Взаимодействия полимер A(B) с полосой B(A) является отталкивательными, и проигрыши в энергии таких взаимодействий равны: ε _AB = ε _BA = 1. Были исследованы цепи различной длины N =32, 64, 128;  расчеты проводились при различной температуре T и различных температурах мутации T_s. Результаты расчетов приведены в параграфе 5.