Физическая модель метода расчета
Для расчета системы используем метод реактивных усилий. Колебания кузова в пространстве определяем по движению центра масс кузова  : тремя линейными
: тремя линейными  и тремя угловыми
и тремя угловыми  его перемещениями по направлению координатных осей кузова
его перемещениями по направлению координатных осей кузова  (рисунок 4.1).
(рисунок 4.1).
Движение всех других частей кузова находим по колебаниям  центра масс кузова и координатам этих частей,
центра масс кузова и координатам этих частей,  .
.
Узел  , движение которого будем изучать, условимся называть центрально-координатным узлом.
, движение которого будем изучать, условимся называть центрально-координатным узлом.
Центрально-координатный узел полагаем имеет внутренние линейные и угловые связи по направлению координатных осей  . Считаем, что все усилия, действующие на рассматриваемое тело, через внутренние элементы-вставки передаются в связи центрально-координатного узла и здесь взаимно уравновешиваются на основании принципа Лангранжа-Деламбера.
. Считаем, что все усилия, действующие на рассматриваемое тело, через внутренние элементы-вставки передаются в связи центрально-координатного узла и здесь взаимно уравновешиваются на основании принципа Лангранжа-Деламбера.
Усилия, которые подходят к узлу, являются активными. Они вызывают в связях реакции:  - сил инерции,
- сил инерции,  - сил упругости,
- сил упругости,  - сил вязкого трения,
- сил вязкого трения,  - возмущающие силы и другие, равные по величине активным силам и противоположно по направленные, где
- возмущающие силы и другие, равные по величине активным силам и противоположно по направленные, где  - номер реакции и номер перемещения.
- номер реакции и номер перемещения.
По видам перемещений кузова колебаниям присвоены названия:
 - колебание подергивания (линейное по оси
- колебание подергивания (линейное по оси 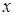 );
);
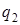 - колебание подпрыгивания (линейное по оси
- колебание подпрыгивания (линейное по оси  );
);
 - колебание бокового относа (линейное по оси
- колебание бокового относа (линейное по оси  );
);
 - колебание бокового поворота (угловое
- колебание бокового поворота (угловое  вокруг оси
вокруг оси 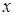 );
);
 - колебание виляния (угловое
- колебание виляния (угловое  вокруг оси
вокруг оси  );
);
 - колебание галопирования (угловые
- колебание галопирования (угловые  вокруг оси
вокруг оси  ).
).
Уравнения колебаний вагона
Уравнения колебаний вагона в общем случае запишутся из уравнений равновесия реакций в центрально-координатных связях кузова:
 (3.3)
(3.3)
Для сил инерции и сил упругости с линейными характеристиками значения реакций  будем записывать через коэффициенты от единичных воздействий:
будем записывать через коэффициенты от единичных воздействий:
 (3.4)
(3.4)
где  - коэффициенты реакций сил инерции и упругости от единичных возмущений:
- коэффициенты реакций сил инерции и упругости от единичных возмущений:  .
.
Уравнения колебаний (3.3) в этом случае можно представить в развернутой записи как систему уравнений вида:
 (3.5)
(3.5)
 2020-01-14
2020-01-14 141
141








